Элементы геометрической оптики и образование изображений на сетчатке

Описание
При изучении процесса формирования оптического изображения точкой изображения считают место наибольшего сужения светового пучка. Обычно имеется в виду изображение, близкое к получаемому в так называемой идеальной оптической системе. При этом изображение точки называют стигматическим, или точечным, или просто резким. При стигматическом изображении все лучи, исходящие из точки и прошедшие оптическую систему, собираются снова в точку. Изображение может быть действительным или мнимым. Действительное изображение — это изображение, образованное реальными лучами. Его можно получить на экране. Мнимое изображение — это как бы «потенциальное» изображение, проявляющееся при определенных условиях. Оно образуется не реальными лучами, а их геометрическим продолжением. Если поставить какой-либо экран в плоскость мнимого изображения, то на нем ничего не изобразится. Но если на пути лучей, идущих от мнимого изображения, находится глаз наблюдателя или объектив фотокамеры, то это мнимое изображение формируется на сетчатке глаза или на фотопленке камеры совершенно так же, как действительное.Пользуясь методами геометрической оптики, рассмотрим образование изображения наиболее распространенными оптическими элементами — отдельными сферическими поверхностями, а затем линзами.
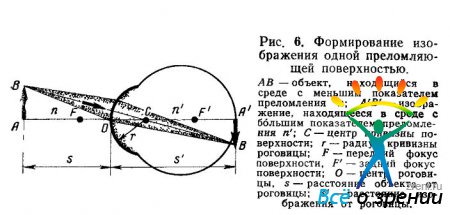
Преломление луча одной сферической поверхностью. Случай, когда изображение формируется одной преломляющей поверхностью, встречается редко. Упрощенная модель глаза — редуцированный глаз (по Гульстранду или Вербицкому) представляет собой именно такое явление. Зная показатель преломления среды и кривизну передней поверхности, играющей роль роговицы, можно найти величину, а также место образования изображения. В этом месте должна находиться сетчатка, чтобы изображение было резким.
В общем случае, когда две среды с разными показателями преломления n и n' разделены сферической поверхностью с радиусом кривизны r и объект АВ находится на расстоянии s от этой поверхности, изображение А'В' будет формироваться на расстоянии s' от нее, определяемом из формулы:
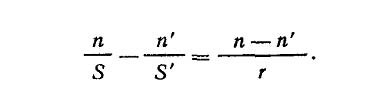
Величина называется оптической силой преломляющей поверхности. Для облегчения оптических расчетов введены понятия фокусов и фокусных расстояний. Если лучи идут из бесконечно удаленной точки, например от звезды, то s = бесконечность и формула принимает вид:
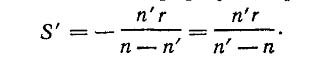
В этом случае s’ является фокусным расстоянием поверхности и обозначается f'.
Если лучи идут от бесконечно удаленной точки, расположенной по другую сторону поверхности, то s =-бесконечность.
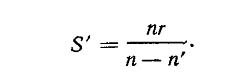
Точка, в которой после преломления сходятся параллельные лучи, т. е. лучи, идущие от бесконечно удаленной точки, называется фокусом сферической поверхности. У сферической поверхности есть два фокуса — передний F и задний F'. Переднее и заднее фокусные расстояния f и f' сферической поверхности не равны между собой, так как не равны показатели преломления сред n и n'.
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
Фокусы, так же как изображения, могут быть действительными и мнимыми. Если вогнутая сторона поверхности раздела обращена к среде с меньшим показателем преломления, то оба фокуса мнимые. Если выпуклая сторона направлена к среде с меньшим показателем, то оба фокуса действительны. Именно такой системой с действительными фокусами является редуцированный глаз.
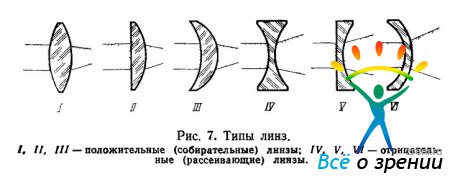
Преломление лучей линзами. В зависимости от формы ограничивающих поверхностей линзы бывают двояковыпуклыми, плосковыпуклыми, двояковогнутыми, плосковогнутыми и выпукловогнутыми. На рисунке линзы I, II и III являются собирательными, или положительными, а линзы IV, V и VI — рассеивающими, или отрицательными. Однако это правильно только для тех случаев, когда материал линзы оптически более плотен, чем окружающая среда, т. е. обладает большим показателем преломления. Если линза состоит из материала с показателем преломления меньшим, чем у окружающей среды, то, наоборот, линзы I, II и III работают как рассеивающие, а IV, V и VI — как собирательные. Так, например, пузырек воздуха в воде работает как рассеивающая линза. Примером линзы, одна поверхность которой находится в менее плотной среде, а другая — в более плотной (водянистая влага), может служить роговица.
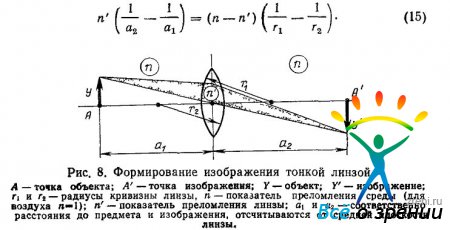
Тонкие линзы. При упрощенных расчетах и геометрических построениях толщиной линз пренебрегают как незначительной. Для таких тонких линз фокусные расстояния до предмета и до изображения отсчитывают от средней плоскости линзы. Это допустимо в случаях, когда толщина линзы мала по сравнению с радиусами кривизны ограничивающих поверхностей. Расстояния от линзы до точки А объекта (a1) и до точки А' изображения связаны между собой зависимостью:
При пользовании формулой нужно принимать во внимание знаки при а1 а2 и r1 r2. Фокусом линзы называют место схождения лучей, падающих на линзу параллельно оси. Плоскость, проходящая через фокус перпендикулярно к оптической оси, называется фокальной плоскостью. Фокусное расстояние линзы можно вычислить, зная rь r2 и п. При ах =—бесконечность (предмет в бесконечность):
Отсюда, если поверхности линз располагаются в одной среде (например, в воздухе), то ее передний и задний фокусы равны по величине и противоположны по знаку, т. е. лежат по разные стороны от линзы: f = —f'. (18)
Толстые линзы. При работе с приборами, имеющими толстые линзы или систему линз (фотообъективы, объективы микроскопов и пр.), во избежание больших ошибок не допускается пользование средней плоскостью. Формулы для расчета положения и размера изображения для сложной оптической системы аналогичны формулам для тонкой линзы, но все расстояния отсчитываются не от средней плоскости, линзы, а от соответствующих кардинальных точек и плоскостей. Кардинальные плоскости — это передняя и задняя фокальные плоскости, передняя и задняя главные плоскости, передняя и задняя узловые плоскости. Соответствующие им кардинальные точки — передний и задний фокусы, передняя и задняя главные, передняя и задняя узловые точки. Когда по обе стороны системы расположена одна и та же среда, то узловые точки сливаются с главными и система характеризуется положением только 4 (вместо 6) точек и плоскостей. Кардинальные точки и плоскости полностью отражают все свойства оптической системы и позволяют пользоваться ею, не рассматривая реального хода лучей в системе.
Фокальные точки и плоскости. Передняя фокальная плоскость — это плоскость, сопряженная с бесконечно удаленной в положительном направлении плоскостью т. е. изображенная в этой плоскости. Точка пересечения
фокальной плоскости с оптической осью является передним фокусом F Задняя фокальная плоскость — это плоскость, сопряженная с бесконечно удаленной в отрицательном направлении плоскостью, а точка ее пересечения с осью называется задним фокусом F'. Если бесконечно удаленный объект находится на оптической оси системы, то идущие от него параллельные лучи после прохождения системы соберутся в ее фокусе. Если же бесконечно удаленный объект расположен не на оси, то пучок параллельных лучей, падающий на систему, составит с осью угол и соберется в точке фокальной плоскости, не лежащей на оси.
Главные и узловые точки и плоскости. Рассмотрим систему с фокусами в точках F и F'. Пусть луч 1 попадает в оптическую систему в точке G и выходит из нее в точке G' Так как луч прошел через точку фокуса, то оп по выходе из системы пойдет параллельно оси Продолжим падающий и выходящий лучи внутри системы (пунктирная линия) Они пересекутся в точке R Плоскость RH, проведенная через эту точку перпендикулярно оси системы, называется передней главной плоскостью, а пересечение этой плоскости с осью (точка Н) — передней главной точкой системы.
Луч 3, параллельный оси, после системы пройдет через задний фокус F' Продолжив падающий и выходящий лучи, получим точку их пересечения R' внутри системы Плоскость R'H', проведенная через точку перпендикулярно оси, будет задней главной плоскостью, а
точка ее пересечения с осью Н' — задней главной плоскостью системы. Плоскости RH и R Нr являются сопряженными. Нетрудно доказать, что линейное увеличение в главных плоскостях равно 1. Расстояние HF между передними главной и фокальной плоскостями есть переднее фокусное расстояние, расстояние между задними главной и фокальной плоскостями — заднее фокусное расстояние. Существенно, что эти расстояния отсчитывают от главных точек, а не от поверхностей линз.
Если плоскости, линейное увеличение которых равно 1, называются главными, то плоскости, в которых угловое увеличение равно 1, называются узловыми. Их пересечение с осью образует переднюю и заднюю узловые точки системы. Любой луч, который направлен в переднюю узловую точку, выйдет из системы параллельно своему первоначальному направлению. Чаще всего пространство предмета и изображения заполнено одним и тем же веществом — воздухом. Тогда главные точки являются одновременно и узловыми точками К и К'. Иногда пространство изображения содержит другое, обычно жидкое, вещество. Примером такой системы является глаз. В подобных случаях узловые точки отличаются от главных и должны быть использованы при построении изображений. При этом особенно интересно следующее свойство узловых точек. Если оптическая система повернулась вокруг оси, проходящей через заднюю узловую точку, то изображение не сдвигается с места Это свойство важно помнить при рассмотрении работы оптической системы глаза.
Определение положения и размера изображения. Если для линзы определены положения главных точек и фокусов, то можно найти положение и размер изображения объекта даже в том случае, когда неизвестны радиусы кривизны и показатели преломляющих поверхностей. Пусть х и х' — расстояния объекта и изображения от соответствующих фокальных плоскостей, а / и )' — переднее и заднее фокусные расстояния. Для определения х и х' пользуются одним из важнейших уравнений геометрической оптики, известного как формула Ньютона:
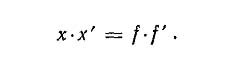
Размер изображения находим из зависимости:
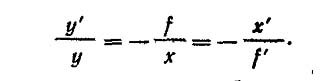
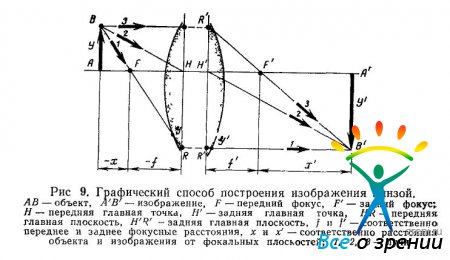
Графическое построение изображения. Легче всего построить изображение графическим способом, который очень нагляден. Достаточно найти точку пересечения двух каких-либо лучей, исходящих из точки предмета. На рисунке показаны лучи, ход которых легче всего определить: луч 3, падающий на линзу параллельно оси, пересечется с осью в заднем фокусе линзы; луч 1, пройдя через передний фокус линзы, идет параллельно оси; луч 2, проходящий через переднюю главную точку линзы, не меняя своего направления, пройдет в пространство изображения, выйдя из задней главной точки. Этот луч называется главным. В случае тонкой линзы он проходит через нее без преломления. Таким образом, если имеется предмет АВ, перпендикулярный оси, то для построения изображения его вершины В проводим из этой точки два луча:
- можно взять лучи 2 и 3. Пересечение их после прохождения через линзу даст точку В' — изображение точки В;
- вместо луча 3 можно взять выходящий из той же точки В луч 1. Пересечение луча 1 с лучом 2 даст ту же точку изображения В'-,
- могут быть использованы лучи 1 я 3. Они пересекутся в той же точке В'.
Изображение на сетчатке. Видимый размер. Оптическая система глаза не стабильна — ее оптическая сила может изменяться в зависимости от удаления объекта.
Получение резкого изображения объектов, расположенных на различных расстояниях от глаза, достигается путем аккомодации — изменения оптической силы глаза. Отметим еще одно различие принципов получения резкого изображения в глазу и фотоаппарате. Если при фотографировании добиваются резкого изображения путем изменения расстояния между объективом и плоскостью пленки, то аккомодация глаза заключается в приспособлении некоторых параметров оптической системы глаза, в основном хрусталика, к расстоянию до наблюдаемого объекта1. Чтобы резко изобразить на сетчатке объект, находящийся на близком расстоянии, комодациодные мускулы напрягаются. Тем самым уменьшается диаметр цилиарного тела, образующего вокруг хрусталика кольцо. Благодаря эластичности оболочки хрусталика при уменьшении растягивающего действия, поверхности хрусталика, преимущественно передняя, становятся более выпуклыми. Изменение формы хрусталика и перемещение слоев с различными показателями преломления внутри хрусталика приводят к уменьшению фокусного расстояния глаза и обеспечивают на сетчатке резкое изображение объектов, расположенных близко от глаза. По действительному изображению на сетчатке глаза невозможно определить истинный размер предметов, так как не известно, на каком расстоянии от глаза они находятся. По размеру сетчаточного изображения можно судить только о видимом размере предмета, соответствующем углу зрения, под которым он виден, т.е. углу между лучами, проведенными из центра зрачка к двум крайним точкам объекта.
Малый объект может иметь тот же видимый размер, что и большой, если он соответственно приближен к глазу. Так, например, размер изображения на сетчатке объекта величиной 12 мм, расположенного на расстоянии 260 мм от глаза, составляет около 1 мм, т.е. имеет такую же величину, как изображение объекта величиной 140 мм, расположенного на расстоянии 5 м от глаза.
Для того чтобы увидеть предмет с максимальным количеством подробностей, нужно добиться получения наибольшего его видимого размера на сетчатке, что соответствует увеличению угла зрения, под которым он виден. Поэтому наблюдатель всегда интуитивно старается приблизить рассматриваемый предмет к глазу. Произвольному приближению, которое могло бы создать любое увеличение видимого размера объекта, ставит предел ограниченная аккомодационная способность глаза.
Аккомодация. Человек молодого возраста в состоянии аккомодировать на расстояние 7—10 см от глаза. При меньших расстояниях человек с нормальным зрением видит лишь размытое изображение. Правда, длительная аккомодация на ближнюю точку сильно утомляет нормальный глаз. Без особого утомления можно наблюдать предметы, находящиеся на расстоянии примерно 250—300 мм. Это расстояние, используемое при всех расчетах оптических приборов, называют условным расстоянием зрения (Р) и принимают равным 250 мм Его можно превзойти, только применяя специальные вспомогательные средства — лупы и микроскопы. Эти оптические приборы дают возможность видеть объект под увеличенным углом зрения, т. е. с большим vrp лечением.
Увеличение. Степень увеличения определяется сравнением увеличеннного угла зрения с углом, под которым объект виден, когда он находится на условном расстоянии зрения — 250 мм от глаза. Отсюда увеличение оптических приборов выражается формулой:
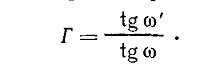
---
Статья из книги: Оптические приборы для исследования глаза | Тамарова Р.М.

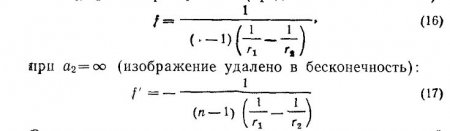

Комментариев 0