Неевклидовость цветового пространства

Описание
Рассмотренные в предыдущих разделах данные различения апертурных цветов обнаружили существенную неевклидовость цветового пространства. Во-первых, данные локального цветоразличения, полученные Мак Адамом, Брауном и Мак Адамом, Райтом и другими авторами в аналогичных работах, показывают, что области дифференциальной чувствительности в пространстве равноярких цветов не могут быть представлены евклидовой квадратичной формой, а только в виде поверхности, имеющей ненулевую гауссову кривизну.Во-вторых, исследования соотношения между едва заметными и надпороговыми различиями (Мак Адам; Джадд, Измайлов) выявляют нелинейность этого соотношения, вызванную неаддитивностью цветоразличения.
В-третьих, данные глобального цветоразличения (Крускел; Шепард и Кэрролл, Измайлов) показывают, что условие глобальной линейности пространства цветоразличения по отношению к воспринимаемым различиям между цветами неизбежно приводит к увеличению размерности евклидова цветового пространства.
Согласование этих разнообразных данных оказывается возможным в рамках сферического пространства цветоразличения, полученного в работах Соколова и др., Измайлова, Соколова, Измайлова, Соколова, Измайлова. Рассмотрим две серии экспериментов по надпороговому различению, проанализированных методом многомерного шкалирования.
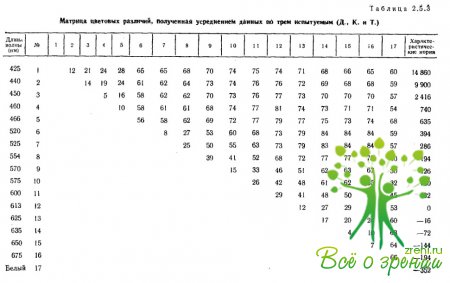
Цветовое пространство монохроматических излучений. В табл. 2.5.3 приведены оценки попарных различий между 16 монохроматическими цветами и белым, полученные в работе Измайлова.
Монохроматические стимулы создавались с помощью узкополосных интерференционных фильтров, а ахроматический стимул — с помощью фотопленки с коэффициентом пропускания, примерно одинаковым для всех длин волн от 400 до 700 им. Все цветовые стимулы были выравнены по светлоте и предъявлялись испытуемым последовательными парами, каждая пара по 10 раз. Эти оценки представляют собой суммарную величину по 10 предъявлениям, усредненную по трем испытуемым.
Анализ матрицы различий проводился метрическим методом многомерного шкалирования по алгоритму Торгерсона. Этот анализ подтвердил, что при заданном условии глобальной линейности между исходными оценками цветовых различий я межточечными расстояниями в цветовом пространстве (т. е. условии полной однородности цветового пространства относительна различий) решением может быть только трехмерное евклидово пространство.
В последнем столбце табл. 2.5.3 приводится собственные значения матрицы, которые характеризуют вклад каждой из осей n-мерного евклидова пространства в структуру цветовых различий. Теоретически минимальная размерность действительного евклидова пространства определяется числом положительных собственных значений, однако вследствие случайных ошибок в исходных данных дополнительно могут появиться небольшие (положительные или отрицательные) собственные значения, поэтому размерность определяется только по числу больших собственных значений.
По данным табл. 2.5.3, видно, что таких значений только три, они на порядок превышают остальные собственные значения. При таком большом формальном вкладе третьего измерения в структуру равноярких цветов пренебречь им можно было бы только в случае наличия веских содержательных аргументов против. Но содержательный анализ полученной конфигурации с точки зрения ее цветовых характеристик показывает, что третье измерение является психофизически значимой цветовой составляющей.
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
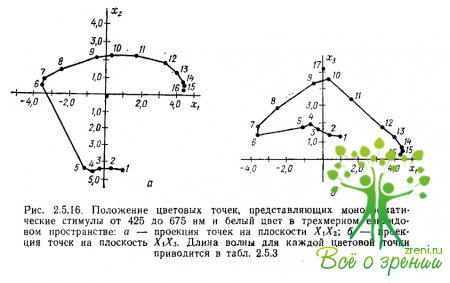
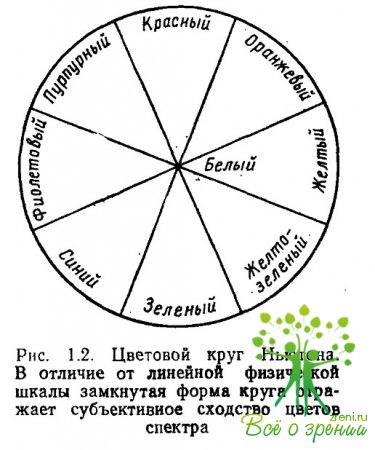
Это иллюстрируется проекцией цветовых точек на две плоскости трехмерного евклидова пространства Х1Х2 и Х1Х3 (рис. 2.5.16а, б). На плоскости Х1Х2 траектория цветовых точек точно соответствует расположению цветов на круге Ньютона, представленном на рис. 1.2.
Это означает, что первые две координаты евклидова пространства определяют цветовой тон стимулов. Проекция точек на плоскость показывает, что третья ось евклидова пространства характеризует ахроматическую составляющую цвета: наибольшее значение этой координаты имеют белый и желтые цвета спектра (точки 17, 9 и 10), а наименьшее значение —красные цвета (точки 14, 15, 16), имеющие почти нулевую ахроматическую компоненту.
Таким образом, не только цветовой тон определяется двумя евклидовыми координатами, но и изменение цветовой насыщенности также определяется двумя взаимоортогональными направлениями в евклидовом пространстве: одно из них представлено радиальным направлением на плоскости Х1Х2, а другое — направлением оси X3.
Сферичность цветового пространства. Главной особенностью приведенной на рис. 2.5.16 а, б конфигурации цветовых точек является то, что они заполняют не все евклидово пространство, а образуют в нем поверхность постоянной положительной кривизны— сферическую поверхность.
Доказательство сферичности полученной многомерным шкалированием конфигурации точек заключается в том, чтобы показать, что для заданной конфигурации точек всегда можно найти геометрический центр, т. е. точку, которая расположена па одинаковом расстоянии от всех имеющихся цветовых точек. При этом между исходными оценками различий и межточечными расстояниями должна сохраняться высокая степень линейной корреляции.
Поскольку расстояния от центра сферы до каждой точки получены из экспериментальных данных, они могут флуктуировать вследствие ошибок в оценках испытуемых. Поэтому на практике ищется такая точка в качестве центра сферы, для которой разброс этих расстояний (радиусов) минимален.
Для поиска применяется итерационная процедура, которая минимизирует стандартное отклонение радиусов, вычисляемых на каждом шаге, от среднего радиуса. В качестве начальной точки берется центр тяжести исходной конфигурации. После нахождения оптимального в указанном смысле центра вся конфигурация точек линейно сдвигается так, чтобы центр сферы совпадал с началом осей координат. Разброс радиусов измеряется коэффициентом вариации в процентах отношения стандартного отклонения к среднему радиусу.
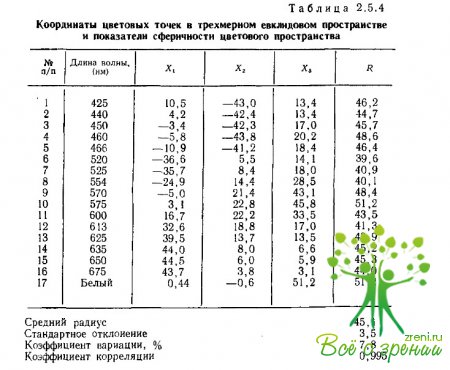
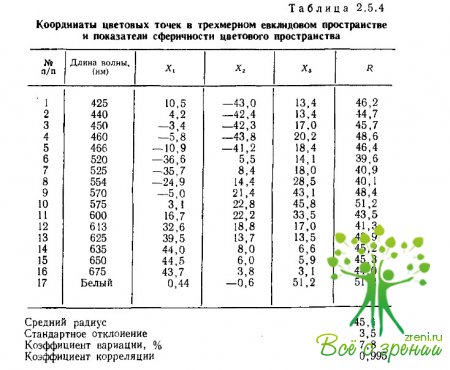
Таким образом, сферичность оценивается по тому, насколько малая вариативность радиусов может быть получена при максимально возможном коэффициенте корреляции между исходными оценками различий и межточечными расстояниями. Приведенные в табл. 2.5.4 данные показывают, что разброс радиусов, т. е. «толщина» сферического слоя, в котором расположены цветовые точки, менее 8% от среднего радиуса. Учитывая высокий коэффициент корреляции (0,995) и величину разброса самих оценок межстимульных различий, которая достигает 10—20% от средней оценки, можно утверждать, что полученная конфигурация точек действительно располагается на поверхности сферы в трехмерном евклидовом пространстве.
Вращение цветового пространства. Полученная система координат цветового пространства не связана в многомерном шкалированиb с конфигурацией точек, поскольку анализ данных проводится в терминах расстояний, которые в евклидовом пространстве не зависят от выбранной системы координат. Выбор системы координат при построении сферического цветового пространства определяется дополнительными ограничениями, которые следуют из цветооппоиентной характеристики цвета.
Для введения этих ограничений предлагается использовать феномен константных тонов спектра, которые рассматриваются как геринговские «чистые» цвета — «синий» (465 нм), «зеленый» (500 нм), «желтый» (575 нм) и «красный» (смесь 440 и 675 нм).
Эти «чистые» цвета образуют две цветооппонентные пары, которые могут определять направление двух взаимоортогональных осей цветового пространства X1 и Х2. Если, например, первую ось пространства ориентировать по красному и зеленому константным тонам спектра, то вторая ось должна быть ориентирована соответственно по синему и желтому константному тонам.
Для получения единственного решения в трехмерном евклидовом пространстве достаточно определить только три точки по отношению к искомой системе координат. Для приведенных в табл. 2.5.3 данных это несложно сделать, например, по стимулам с длиной волны 486, 575 и 650 нм. Полученные в результате такого вращения координаты цветовых точек в трехмерном евклидовом пространстве приведены в табл. 2.5.4.
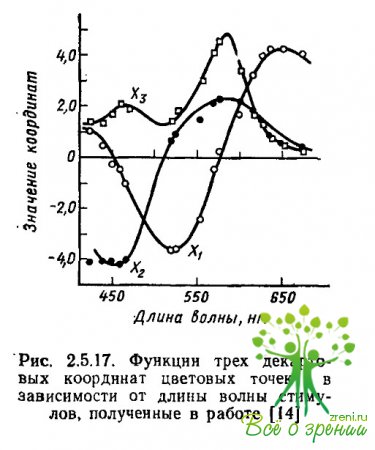
На рис. 2.5.17 показаны функции, которые характеризуют полученные оси координат относительно монохроматических излучений равной яркости. Две из них — Х1 и Х2 — согласуются с красно-зеленой и сине-желтой оппонентными функциями, полученными в работе Харвича и Джемсон и приведенными на рис. 2.5.18. Третья функция — Х3 представляет собой характеристику, обратную функции насыщенности спектральных цветов, полученной в работе Мартина и др. В связи с этим она получила название функции белизны равнояркого спектра.
Нормирование цветовой сферы. Особое внимание необходимо- обратить в данном случае на отсутствие систематических сдвигов- в флуктуации радиусов цветовых точек (табл. 2.5.4). Это означает, что этими флуктуациями можно пренебречь как ошибками,, связанными со случайными помехами в экспериментах. Нормирование координат цветовой точки по ее радиусу позволяет представить все цвета точками на поверхности единичной сферы:
Сферическое пространство смешанных цветов. Результаты шкалирования надпороговых различий между смешанными цветами описываются в работах Соколова и Измайлова. Цветовые стимулы формировались на экране цветного телевизора путем комбинации напряжений на трех электронных пушках кинескопа. Оценки попарных цветовых различий, усредненные по 15 предъявлениям каждой пары, приводятся в табл. 2.5.5.
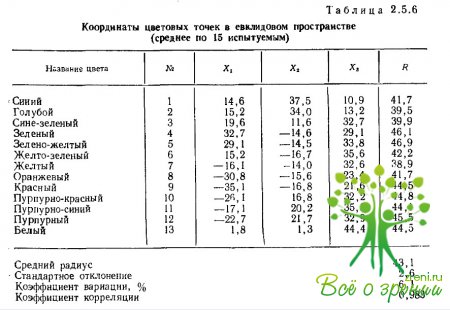
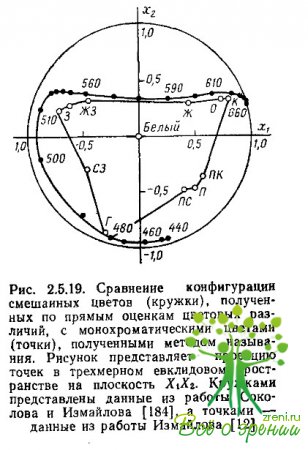
Пространство цветоразличения, полученное в результате анализа матрицы различий метрическим методом многомерного шкалирования, по своей структуре совершенно идентично пространству монохроматических цветов. Смешанные цвета располагаются также па поверхности сферы в трехмерном евклидовом пространстве, и их положение согласуется с законами смешения цветов (табл. 2.5.6, рис. 2.5.19).
Сферическое цветовое пространство, построенное по данным называния цветов». К аналогичным результатам приводит также анализ методом многомерного шкалирования данных называния цветов.
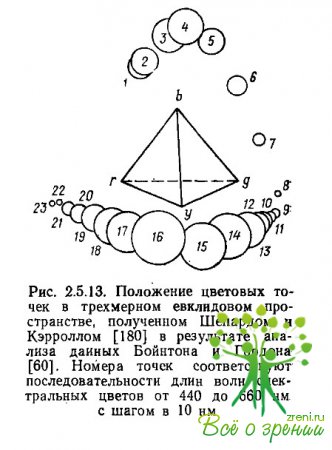
Рассматривая ранее исследование Шепарда и Кэрролла, мы уже видели, что условие глобальной линейности, накладываемое на связь межточечных расстояний с исходными мерами «близостей» между цветами, приводит к трехмерному решению. Однако точки, представляющие монохроматические цвета, располагаются в трехмерном пространстве на одномерной кривой; они упорядочены в соответствии с последовательностью длин волн в спектре (рис. 2.5.13).
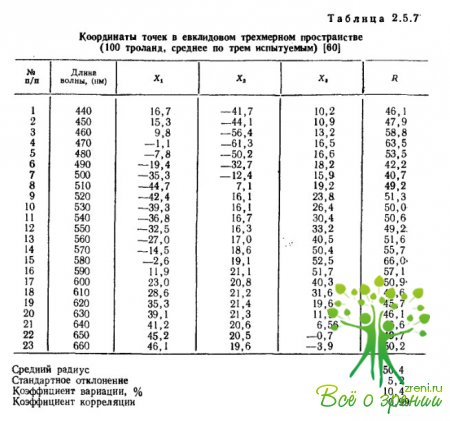
В работе Измайлова показано, что точки этой кривой с большой точностью описываются уравнением сферы в трехмерном евклидовом пространстве (табл. 2.5.7 и рис. 2.5.19). В работе техника, предложенная Шепардом и Кэрроллом, применялась к данным называния цветов, среди которых были не только монохроматические, но и белые цвета разной яркости.
Исходные данные, полученные методом называния цветов, отличались от данных Бойнтона и Гордона тем, что для классификации применялось не четыре класса (красный, желтый, зеленый, синий), а пять — был добавлен еще один класс названий (белый). Кроме того, при классификации позволялось использовать не только одинарные или двойные комбинации названий («красный» или «желто-красный»), но и тройные (например, «желто-бело-красный» или «бело-сине-зеленый» и т. д.).
Результаты этого исследования показали, что цвета, различающиеся одновременно по тону, насыщенности и светлоте, можно расположить только в четырехмерном евклидовом пространстве, если исходить, как и для равноярких цветов, из условия линейного соответствия между цветовыми различиями и межточечными, расстояниями.
Множество всех цветовых точек, как и в случае: равноярких цветов, располагалось на поверхности трехмерной, сферы так, что одна сферическая координата точки соответствовала цветовому тону, другая — цветовой насыщенности, и третья — светлоте цвета. Каждое подмножество равноярких цветов в четырехмерном евклидовом пространстве располагалось в трехмерном евклидовом подпространстве, изоморфном трехмерному пространству, полученному отдельно для равноярких цветов.
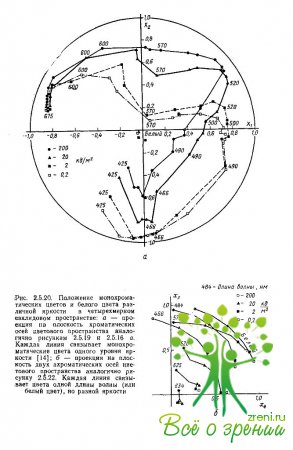
На рис. 2.5.20а приводится проекция всех цветовых точек, и монохроматических и белых в том числе, на плоскость двух первых (хроматических) координат четырехмерного евклидова пространства,, аналогично данным, полученным по оценкам прямых цветовых различий и по данным называния цветов для равноярких цветов, (рис. 2.5.19).
Цветовые точки, представляющие один и тот же монохроматический стимул на разных уровнях яркости, могут существенно различаться по своему положению в хроматическом подпространстве (например, точки, представляющие стимул с длиной волны 570 нм, или 490 нм иа рис. 2.5.20 а), а могут и сливаться в одну точку (например, для стимулов с длиной волны 650 нм, или для нейтральных цветов, которые спроецированы в точке пересечения осей координат).
Но независимо от этого они по своим ахроматическим характеристикам могут также различаться или не различаться, как это иллюстрируется рисунком 2.5.20 б, где показана проекция монохроматических цветов и белого разных уровней яркости на плоскость ахроматических координат четырехмерного цветового пространства.
Таким образом можно сделать вывод, что цветоразличение характеризуется достаточно сложной структурой и не может рассматриваться в рамках каких-либо частных цветовых характеристик, например, только тона и насыщенности, или только цветооппонентных функций и т. д. При анализе цветоразличения необходимо учитывать структуру всего цветового пространства, включающего все характеристики апертурных цветов.
Возможность такого общего подхода к построению цветового' пространства дает метод многомерного шкалирования больших цветовых различий. Преимущества этого подхода заключаются не только в системности описания цветоразличения, но и в существенной апостериорности полученного решения. При построении цветового пространства исследователь исходит только из одного условия— глобальной линейности между цветовыми различиями и межточечными расстояниями.

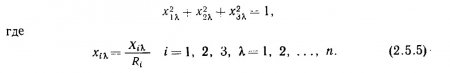


Комментариев 0