Очковая оптика | Часть 1
Описание

Скорость распространения света в различных средах неодинакова. Быстрее всего свет распространяется в безвоздушном пространстве (скорость его равна приблизительно 300 000 км/сек.). Чем плотнее среда, тем медленнее в ней распространяются лучи света. В воздухе скорость света равна приблизительно скорости его в безвоздушном пространстве, в воде — около 225 000 км/сек., в стекле — около 200 000 км/сек.
Свет в оптически однородной среде распространяется по прямым линиям; при переходе света из менее плотной среды в более плотную (или наоборот) луч света отклоняется от прямолинейного направления. Плотность среды характеризуется показателем преломления. Последний представляет собой отношение скорости света в безвоздушном пространстве (или в воздухе) к скорости света в данной среде, а так как скорость распространения света в любой среде медленнее, чем в безвоздушном пространстве, то показатель преломления всякой среды будет больше единицы.
Для воды он равен:
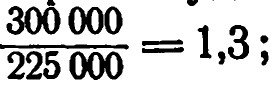 ; для стекла он равен:
; для стекла он равен: 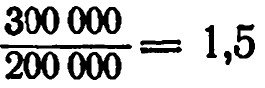 *; для стекловидного тела глаза равен 1,336.
*; для стекловидного тела глаза равен 1,336.* В зависимости от химического состава стекла показатель преломления его колеблется от 1,464 до 1,608.
Отклонение луча света от прямолинейного направления, наступающее при переходе Луча из среды с одним показателем преломления в среду с другим показателем, называется преломлением света.
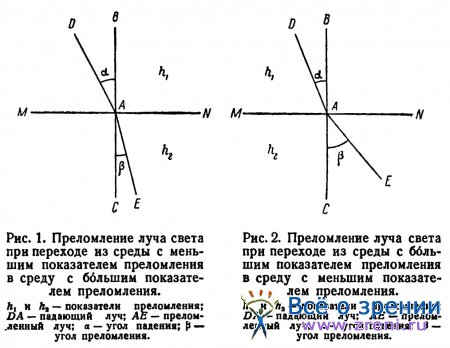
Если к поверхности раздела между двумя средами К и (рис. 1 и 2) в месте падения луча света А восставить перпендикуляр ВАС, обозначить линией DA падающий луч и линией АЕ — луч преломленный, то угол а будет углом падения, а угол Бетта — углом преломления.
Характер преломления света будет зависеть от разницы в показателях преломления. Если луч света вступает из среды с меньшим показателем преломления в среду с большим показателем, т. е. Aj меньше h2, то угол преломления будет меньше угла падения и луч света приблизится к перпендикуляру ВАС (рис. 1). При обратном отношении, когда луч света вступает из среды более плотной в менее плотную, т. е. h1 больше h2, угол преломления будет больше угла падения и луч света отдалится от перпендикуляра ВАС (рис. 2). В обоих случаях разница между углом падения и углом преломления тем больше, чем больше разница между показателями преломления сред, в которых свет распространяется.
Большое значение для преломления света, кроме разницы в показателях преломления сред, имеет форма пограничных поверхностей между обеими средами.
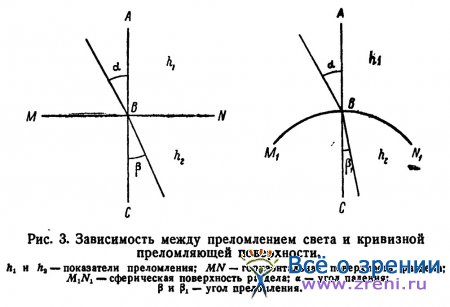
Если h2 больше, чем h1 а поверхность раздела в одном случае будет плоская, а в другом сферическая (рис. 3), то во втором случае отклонение луча при переходе из одной среды в другую будет более резким, чем в первом, и угол преломления бетта будет меньше угла падения альфа.
Зависимость между преломлением света и кривизной преломляющей поверхности выражается в том, что преломление света усиливается по мере уменьшения радиуса кривизны преломляющей поверхности. Таким образом, преломление света тем больше, чем больше разница в показателях преломления сред, в которых свет распространяется, и чем меньше радиус кривизны преломляющей сферической поверхности.
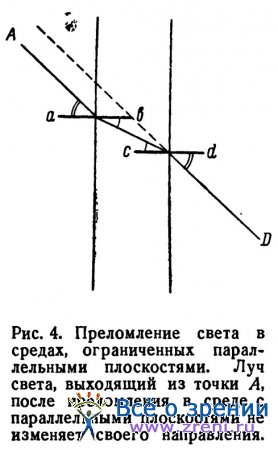
Если луч света проходит через среду, ограниченную параллельными плоскостями, то направление выходящего луча параллельно направлению падающего луча (рис. 4).
Если в точке D находится глаз, то точка А, находящаяся по ту сторону стеклянной пластинки, кажется передвинутой в сторону. Чем острее угол, под которым глаз смотрит через стекло, тем сильнее смещение точки, из которой выходит луч, но сам луч обязательно имеет направление, параллельное падающему лучу.
Луч света, проходя через призму, преломляется по направлению к основанию призмы (при входе в призму он приближается к перпендикуляру, восставленному к точке падения луча, при выходе удаляется от перпендикуляра, восставленного к точке его выхода).
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
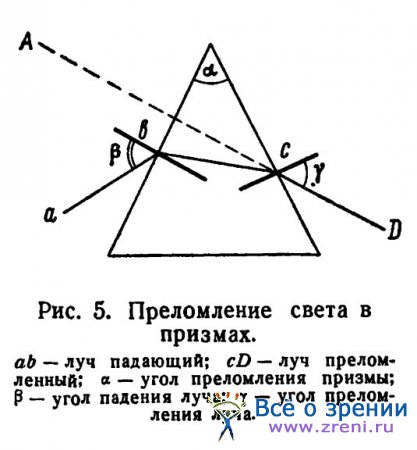
Если глаз смотрит на какой-нибудь предмет через призму, то этот предмет кажется ему отклоненным к преломляющему углу призмы (рис. 5).
Если глаз, находящийся в точке D смотрит на предмет а, то он видит этот предмет смещенным в точку А.
Величина отклонения зависит от величины преломляющего угла призмы альфа, от величины угла падения бетта и показателя преломления среды, т. е. материала, из которого сделана призма.
Из двух последних рисунков и объяснительного текста к ним видно, что среды, ограниченные параллельными плоскостями оптически недеятельны, они не изменяют направления проходящих через них лучей; только среды, имеющие строение призмы, преломляют проходящие через них лучи, отклоняя их в сторону основания призмы.
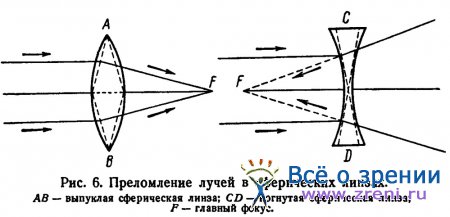
В физике считается, что оптическое действие сферических линз зависит от того, что они имеют скрытое строение призмы. Выпуклая линза как бы состоит из двух призм, соединенных вместе основаниями. Каждая призма будет преломлять падающие на нее лучи в сторону основания призмы, т. е. к оптической оси линзы, где и будут собираться в фокусе преломленные в линзе лучи. Вогнутая линза состоит из призм, соединенных вместе вершинами; каждая призма будет преломлять падающие на нее лучи в направлении к основанию призмы (рис. 6), получится рассеивающее действие линзы; лучи будут расходящимися.
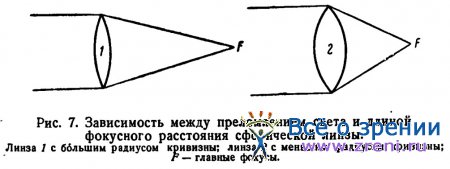
Величина преломляющей силы может быть определена на основании измерения фокусного расстояния. Если мы возьмем две двояковыпуклые линзы, сделанные из стекла с одним и тем же показателем преломления, но с разной кривизной преломляющих поверхностей (рис. 7), то, на основании вышеизложенного, линза, поверхность которой будет иметь меньший радиус кривизны, будет обладать большей преломляющей силой.
Поэтому параллельные лучи после преломления во второй линзе (рис. 7) сильнее отклонятся от своего первоначального направления и соберутся в точке, расположенной ближе к линзе, т. е. эта линза будет иметь более короткое фокусное расстояние, чем линза первая. Параллельные лучи в первой линзе преломятся слабее и соберутся в точке, более далеко отстоящей от линзы. Отсюда видно, что между преломляющей силой линзы и длиной ее главного фокусного расстояния существует обратно пропорциональная зависимость, выражаемая следующей формулой:
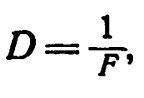
где F обозначает длину главного фокусного расстояния, a D — преломляющую силу. Эту формулу следует читать так: преломляющая сила оптической системы обратно пропорциональна главному фокусному расстоянию.
Преломляющая сила измеряется в диоптриях. В качестве единицы измерения предложено стекло с фокусным расстоянием в 1 метр. Преломляющая сила такого стекла равна одной диоптрии, как это видно из следующего расчета:
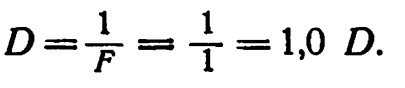
Для линз с фокусным расстоянием в 0,5 м (50 см), 0,4 м (40 см ), 0,25 м (25 см) и т. д. преломляющая сила будет соответственно равна 2,0 D; 2,5 D; 4,0 D и т. д. Для стекол с фокусным расстоянием в 2 м, 4 м преломляющая сила будет 0,5 D; 0,25 D. Следовательно, зная фокусное расстояние стекла, мы получаем его преломляющую силу в диоптриях; зная преломляющую силу стекла в диоптриях, легко находим его фокусное расстояние. В первом случае надо 1 разделить на линейную величину, соответствующую фокусному расстоянию, выраженному в метрах, во втором случае надо 1 разделить на число, выражающее преломляющую силу стекла в диоптриях.
Гульстранд расширил понятие о диоптрии, и, по его предложению, диоптриями измеряют не только преломляющую силу оптических систем, но и конвергенцию падающих и преломленных лучей. Если на линзу + 2,0 D падают параллельные лучи, которые после преломления в линзе соберутся в главном фокусе на расстоянии 0,5 м от стекла, то степень конвергенции преломленных лучей будет также 2,0 D. Если возьмем линзу + 4,0 D, то параллельные лучи после преломления в этой линзе соберутся в главном фокусе уже на расстоянии в два раза короче, т. е. в 0,25 м от стекла. Конвергенция этих преломленных лучей будет в два раза сильнее, т. е. 4,0 D. Степень конвергенции лучей и фокусное расстояние — величины обратно пропорциональные. Следовательно, под 1,0 D подразумевают не только величину, обратную фокусному расстоянию, но и величину степени конвергенции падающих и преломленных лучей.
Измерение главного фокусного расстояния, равно как измерение ряда других расстояний в оптической системе, производят от главных плоскостей системы. В каждой линзе, в каждой оптической системе имеются две главные плоскости, из которых одна — передняя, другая — задняя. Эти плоскости являются сопряженными и удовлетворяют следующим соотношениям: величина объекта в первой из них равна величине изображения во второй; при этом во второй главной плоскости получается прямое изображение. Главные плоскости перпендикулярны к главной оптической оси и пересекают ее в главных точках. Главная оптическая ось представляет собой прямую линию, проходящую через центры кривизны всех преломляющих сред системы.
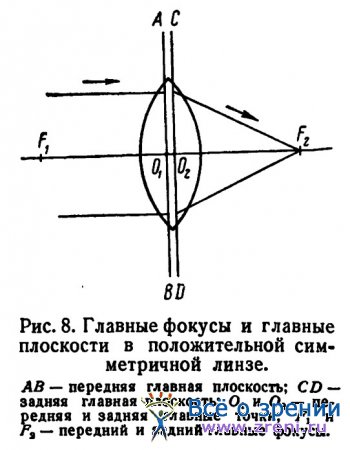
Для примера возьмем симметричную двояковыпуклую линзу (равновыпуклые и равновогнутые сферические линзы называются симметричными линзами). В такой линзе обе главные плоскости проходят внутри линзы на равном расстоянии от поверхности стекла — первая ближе к объекту, вторая ближе к изображению (рис. 8). Переднее фокусное расстояние измеряется от передней главной плоскости, заднее — от задней главной плоскости.
Фокусное расстояние и, следовательно, преломляющую силу оптических систем расценивают не только по величине, но и по знаку.
В оптике при всех вычислениях принято считать, что источник света находится слева и что все расстояния всегда исчисляются от оптической системы до
светящейся точки или до объекта, причем установлено, что все расстояния, идущие по направлению падающего луча, т. е. слева направо, положительные, а расстояния, отсчитываемые в обратном направлении, — отрицательные.
Возьмем двояковыпуклое стекло. Параллельные лучи, идущие слева направо, после преломления в двояковыпуклом стекле собираются в заднем главном фокусе F2 (рис. 8), за стеклом. Фокусное расстояние (02F2) измеряется от задней главной плоскости до главного фокуса в направлении падающего луча света, т. е. слева направо, поэтому оно положительное, и преломляющая сила этой линзы будет величиной положительной:
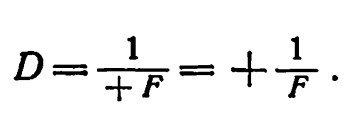
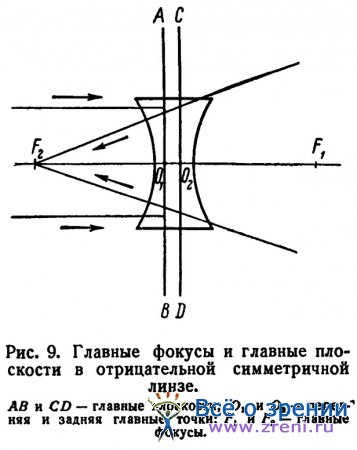
В двояковогнутой линзе параллельные лучи, идущие слева направо, после преломления в ней становятся расходящимися и кажутся исходящими из точки мнимого их пересечения F2; эта точка называется задним главным фокусом, она расположена впереди стекла на той же стороне, откуда исходит свет; фокусное расстояние (02F2) измеряется от задней главной плоскости до точки F2 справа налево, против направления падающего луча света, поэтому оно отрицательное, и преломляющая сила этой линзы будет величиной отрицательной.
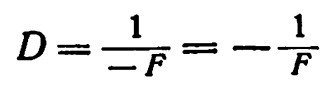
При оценке знака конвергенции лучей поступают аналогичным образом: если точка конвергенции лежит вправо от линзы, то конвергенция будет положительной (со знаком +), если влево, то отрицательной (со знаком —) (см. рис. 9).
Отсюда понятно, почему двояковыпуклые линзы обозначаются знаком плюс (+), а двояковогнутые — знаком минус (—).
В оптике допускается измерение преломляющей силы (рефракции) оптических систем не от главных точек, а от преломляющей поверхности; такая рефракция названа вершинной рефракцией в отличие от главной рефракции, которая измеряется от главных точек.
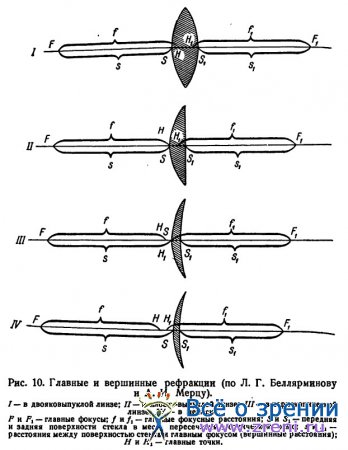
Для иллюстрации положения главных точек и разницы между главной и вершинной рефракциями в различных линзах на рис. 10 приведены соответствующие схемы.
При взгляде на рис. 10 бросается в глаза разница между главной и вершинной рефракциями в выпуклых, плоско-выпуклых и выпукло-вогнутых стеклах.
Особенно велика эта разница при сравнении двояковыпуклой линзы и мениска. В двояковыпуклой линзе главные точки расположены в толще стекла, в мениске же они помещаются вне стекла, впереди него. Такая же разница при сравнении двояковогнутой линзы и отрицательного мениска, в последнем главные точки будут расположены также вне стекла, но только позади него.
В оптической системе, кроме главных точек, существуют две узловых точки. Последние характеризуются тем, что луч, падающий на систему в направлении одной из них, после прохождения через все преломляющие среды, не преломляясь, дальше продолжает идти по тому же направлению, но смещенным из второй узловой точки; так как две узловые точки расположены в системе очень близко друг к другу, то принято для упрощения системы и без особой погрешности считать их за одну узловую точку, через которую все падающие в глаз лучи проходят не преломляясь.
Из всего изложенного выше можно прийти к следующему заключению. Каждая оптическая система характеризуется шестью основными точками: передний и задний главные фокусы, передняя и задняя главные точки и две узловых точки. Эти шесть точек называются кардинальными.
Между положением объекта и расположением изображения существуют определенные взаимоотношения, так что данному положению объекта всегда соответствует определенное расположение изображения его. Всякому перемещению объекта по отношению к линзе (или другой оптической системе) соответствует и перемещение изображения. С определенным положением объекта в пространстве связаны также и размеры изображения и его характер. Изображение может быть увеличенным и уменьшенным; прямым и обратным; действительным и мнимым. Разница между действительным и мнимым изображением состоит в том, что первое может быть получено на экране, а второе не получается, первое располагается в области действительного пересечения лучей, а второе воображаемое, несуществующее, строится в области мысленного пересечения лучей. Для того чтобы найти размеры и расположение изображения, получаемого от объекта при помощи какой-либо оптической системы, вполне достаточно для построения знания шести кардинальных точек.
В основу этого построения положены следующие основные законы оптики.
1. Луч, идущий параллельно главной оптической оси, после преломления проходит через главный фокус.
2. Луч, проведенный через главный фокус, после преломления идет параллельно главной оптической оси.
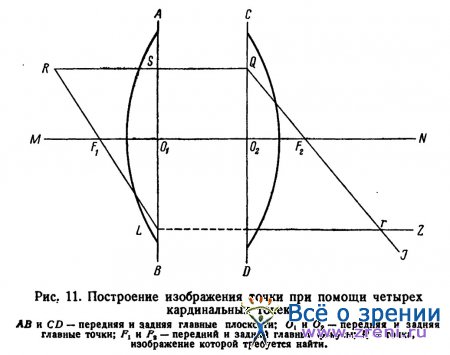
3. Луч, пересекающий одну из главных плоскостей на определенном расстоянии от главной оптической оси, пересекает вторую главную плоскость в точке, расположенной на том же расстоянии от главной оси (рис. 11).
Пусть MN будет главная оптическая ось сферической линзы (двояковыпуклой), АВ и CD — передняя и задняя главные плоскости, пересекающие главную ось в точках O1 и О2; F1 и F2 — передний и задний главные фокусы и R — точка, изображение которой требуется найти.
Для построения изображения проводятся два луча из точки R до первой главной плоскости: один — RS— параллельно оптической оси и второй — RL — через передний главный фокус F1. Первый луч, как параллельный оптической оси, должен пройти после преломления через задний фокус, т. е. из точки Q, расположенной во второй главной плоскости на том же расстоянии от оптической оси, как и точка 5 в передней главной плоскости, через точку F2 (на рис. 11 QF2). Второй луч, прошедший через передний фокус, пойдет после преломления параллельно оптической оси в виде линии LZ. Изображение точки R будет в точке r на месте пересечения двух линий LZ и QF2.
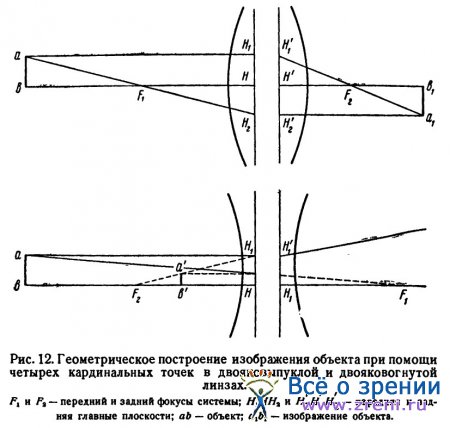
Построение изображения объекта при помощи четырех кардинальных точек в двояковыпуклых и двояковогнутых линзах показано на рис. 12.
Луч, проведенный из точки а параллельно оптической оси, пересекает главные плоскости на высоте H1 и Н1/1, и дальше идет через задний главный фокус F2. Второй луч из точки а, проведенный через передний главный фокус F1 до пересечения с передней главной плоскостью в точке H2, пересекает дальше заднюю главную плоскость в точке Н1/2 и дальше идет параллельно оси. Пересечение обоих лучей в точке a1 дает изображение точки а. Можно также получить изображение точки b и, следовательно, получить изображение предмета аb.
Положение изображения может быть найдено и без построения путем расчета, если известны следующие две величины: фокусное расстояние линзы и расстояние объекта от передней главной плоскости.
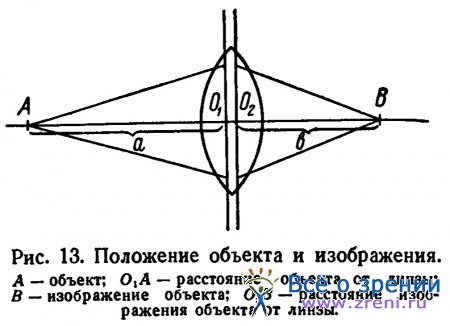
Предположим, что на линзу падает от какого-то объекта расходящийся пучок лучей света (рис. 13).
Расстояние объекта А от линзы О1А назовем а; так как это расстояние отсчитывается от линзы влево, то оно будет со знаком минус (—). Расстояние до точки В(02В), в которой собираются лучи после преломления в линзе и где получается изображение объекта, назовем b; оно лежит вправо от линзы, т. е. будет со знаком плюс (+). Сообразно сказанному выше, следует принять, что конвергенция падающего и преломленного пучков света есть величина, обратная расстояниям до объекта и его изображения, поэтому конвергенция падающего пучка света будет равна:
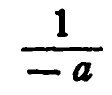 ; назовем эту величину — А, т. е. конвергенция отрицательная; конвергенция преломленного пучка будет
; назовем эту величину — А, т. е. конвергенция отрицательная; конвергенция преломленного пучка будет 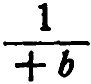 ; назовем ее +В.
; назовем ее +В.При одной и той же степени конвергенции падающего пучка света конвергенция преломленного пучка будет зависеть от преломляющей силы линзы. При одной и той же преломляющей силе линзы степень конвергенции преломленного пучка будет зависеть только от расстояния объекта от линзы, т. е. зная А (степень конвергенции падающих лучей) и D (преломляющую силу линзы), можно определить В (степень конвергенции преломленного пучка света), а, значит и расстояние до изображения объекта. Эти три величины связаны следующей формулой:
В = A + D
Пример 1. Преломляющая сила линзы +4,0 D. Расстояние объекта от линзы — 50 см. Где лежит изображение?
Изображение лежит в 50 см за линзой.
Пример 2. Объект находится на расстоянии 10 см от линзы. Преломляющая сила линзы + 5,0 D. Где лежит изображение?
Изображение лежит на расстоянии — 20 см, т. е. перед линзой (влево от нее); таким образом, оно является мнимым.
Пример 3. Объект расположен перед вогнутой линзой в — 5,0 D, на расстоянии 1 м. Где лежит изображение?
Изображение лежит на расстоянии — 16,7 см, т. е. перед линзой (влево от нее); таким образом, изображение является мнимым.
Продолжение статьи в "Очковая оптика | Часть 2".
---
Статья из книги: Пособие по подбору очков | Галкин Н.Н.


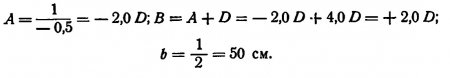
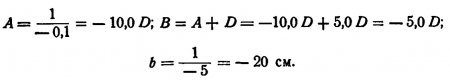
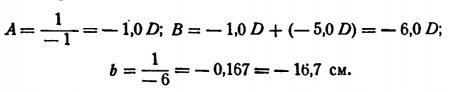
Комментариев 0