Вооруженный глаз

Описание

↑ Приборы, работающие совместно с глазом

Из огромного разнообразия оптических инструментов нас будут интересовать только приборы, которые работают вместе с глазом, образуя единую систему, вооружая глаз.

Собственно, один из видов таких приборов мы уже рассмотрели— это очки. Но очки только помогают сфокусировать на сетчатке изображение предметов, которые нормальный глаз фокусирует и без помощи прибора. Настоящее вооружение глаз дает возможность увидеть то, что недоступно невооруженному глазу. Действие его в основном сводится к созданию на сетчатке изображения, размеры которого больше, чем они были бы без прибора. Приборы, вооружающие глаз, характеризуются увеличением, обычно большим единицы.

Если необходимо изучать объекты, очень малые по абсолютному размеру, прибегают к микроскопу. Если объекты очень удалены и потому малы их угловые размеры, помогает телескоп.

↑ Микроскоп

Пусть подлежащие изучению детали объекта имеют линейный размер h, настолько малый, что h/l0 ? С 3 • 10-4, где l0 = 250 мм — расстояние наилучшего зрения, а 3•10-4 ? 1'. Чтобы сделать угол ?, под которым видна деталь, большим 1', следует значительно уменьшить расстояние объекта от глаза; но тогда мы не сможем сфокусировать изображение объекта на сетчатке. Помочь может собирающая линза с малым фокусным расстоянием f. Поместив объект в се фокус, мы сможем приставить глаз к линзе и получить на сетчатке четкое изображение предмета. Угол ? будет теперь уже не h/l0, a h/f, т. е. увеличится в l0/f раз. Такая линза, называемая лупой, дает увеличение Г = l0/f.

Если нужно получать большие увеличения, применяют микроскоп — систему, состоящую из объектива и окуляра. Предмет помещают немного дальше передней фокальной плоскости объектива и получают действительное увеличенное изображение его в фокальной плоскости окуляра, который работает как лупа. Если фокусное расстояние объектива fb, а окуляра fk, причем расстояние между фокусами внутри трубы lт, микроскоп дает увеличение



При малых fb и fk и большой длине lТ увеличение Г можно сделать очень большим, скажем две-три тысячи. Однако мы не можем безгранично уменьшить h — размер видимой в микроскоп детали. Этому препятствует дифракция. Еще различаемая в микроскоп деталь не может быть значительно меньше длины волны используемого света ?. Формула для предельно разрешающего размера такова
[banner_centerrs] {banner_centerrs} [/banner_centerrs]



где n — показатель преломления среды, в которую погружены объект и переднее стекло объектива; u — угол между осью объектива и крайним, входящим в него лучом. В современных объективах u доводится почти до 90°, а n ? 1,5. Поэтому можно считать, что



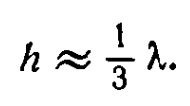
На расстоянии 25 см глаз разрешает размер h0 ? 0,07 мм (считаем, что предельный угол ? ? 1' ? 3*10-4). А одну треть длины волны видимого света можно принять за h = 1,8*10-4 мм. Отсюда



Итак, рациональное увеличение для микроскопа, работающего в видимом свете, 400—500. При значительно больших увеличениях наблюдатель не увидит никаких новых деталей объекта, но может увидеть то, чего в объекте нет: дифракционную картину, создаваемую объектом.

Следует заметить, что освещенность изображения на сетчатке падает пропорционально квадрату Г. Поэтому в микроскопе требуется создавать очень большие освещенности объекта и максимально использовать свет, улавливая его в широком апертурном угле u. Чем больше будет уловленный поток, тем в конечном счете большую информацию получим мы об объекте.

↑ Телескоп

Как показывает само название, телескоп предназначен для изучения далеких объектов. Их в подавляющем большинстве случаев мы не можем освещать (использование прожекторов — сравнительно редкий случай). И для того чтобы собрать от далекого объекта достаточно много света, остается один путь: применение большого объектива, большой диаметр входного зрачка D. Большой входной зрачок — это и есть основное достоинство телескопа. Напомним, что разрешающая сила телескопа прямо пропорциональна D [см. формулу (155)]. Существует, однако, ряд причин, ограничивающих величину D. Во-первых, назначение прибора накладывает ограничение на его габариты: вряд ли будет удобен, например, бинокль с полуметровыми объективами. Во-вторых, чем больше объектив, тем труднее обеспечить хорошее качество даваемого им изображения. Наибольшие объективы применяются в астрономических телескопах.

Уловленные большим входным зрачком световые потоки необходимо рационально использовать, т. е. влить в глаз, имеющий малый зрачок, диаметр которого dr. Сжатие пучка света, входящего в объектив, достигается с помощью увеличения Г. Сохраняя символы, примененные для микроскопа, для телескопа можно написать



где D' — выходной зрачок телескопа; ? и ?' угловой размер наблюдаемого объекта в пространстве предметов и в пространстве изображений соответственно; ? — половина угла поля зрения объектива, а ?'— окуляра. Разрешающая сила телескопа пропорциональна D [см. формулу (155)]. Для того чтобы весь свет, собранный объективом, вливался в глаз, необходимо соблюдение условия D' ? dr. Если D' = dr увеличение называют равнозрачковым и обозначают Гр. Теоретически Гр — наилучшее увеличение: весь свет попадает в глаз, и все, что разрешается объективом, разрешается глазом.

При Г меньше Гр увеличение недостаточно, чтобы глаз воспринял все детали, разрешаемые объективом. Разрешающая сила системы глаз плюс оптический прибор занижена. Объясняется это тем, что в глаз попадает не весь свет, собранный объективом. Действующий диаметр объектива в этом случае равен диаметру зрачка глаза, умноженному на увеличение (drГ), т. е. он меньше, чем D.

Если Г больше Гр, световой поток на сетчатке распределяется по слишком большой площади, что приводит к уменьшению видимой яркости предметов.

Учтем теперь отличное от единицы пропускание системы тс и подытожим результаты. Яркость объекта назовем L, а яркость, видимую в телескоп, L'. При любом увеличении ?' = ?Г; tg ? = tg ?'/Г.



где ? — предельный угол разрешения системы глаз — телескоп в центре поля зрения.

На практике увеличение редко бывает разнозрачковым, прежде всего в силу того, что диаметр зрачка dr — величина переменная [см. формулу (22) ]. С падением яркости зрачок расширяется и желательно, чтобы выходной зрачок прибора все же не оказывался меньше зрачка глаза. Ведь при наблюдении в сумерках особенно важно избежать добавочных потерь яркости. Большой выходной зрачок имеет и другие преимущества: его легче находить (совмещать с ним глаз). Кроме того, заниженное (по сравнению с Гр) увеличение обеспечивает большее поле зрения объектива [см. формулу (179)]. Некоторое снижение разрешающей способности [см. формулу (180) при Г меньше Гр] допустимо по следующим соображениям. Современные телескопические приборы исправлены настолько, что обеспечивают теоретическую разрешающую силу, но только в центре поля зрения. При удалении от оси системы разрешающая сила довольно быстро надает. И для большей части поля зрения Гр оказывается преувеличенным. Поэтому у современных биноклей Г меньше Гр.

Проведенные до сих пор рассуждения относятся к наблюдению протяженных объектов. Наблюдение точечных источников света связано с некоторыми особенностями. Типичный пример точечного источника — звезда. Угловые размеры звезд настолько малы, что даже при большом увеличении ? < 1'. При любом увеличении площадь изображения звезды на сетчатке практически остается одинаковой. Нужно только, чтобы весь свет входил в зрачок глаза, т. е. чтобы соблюдалось условие Г ? Гр. Раз это условие соблюдено, блеск звезды наблюдаемый в телескоп, связан с ее блеском Е зависимостью



Хотя Е' не зависит от увеличения (если Г больше ГР), практически выгодно, однако, делать Г значительно больше Гр. Дело в том, что при Г больше Гр уменьшается видимая яркость протяженных объектов, т. е. фона, на котором видна звезда, что приводит к понижению порогового блеска и к лучшей видимости звезды.

Как известно, блеск звезды характеризуется звездной величиной m. Переходу от m к m + 1 соответствует уменьшение блеска в 2,5 раза. Предельная величина mп звезды, которую в благоприятных условиях видит человек с хорошим зрением, равна 6,5. Для телескопов доступны звезды значительно большей звездной величины. Предельная звездная величина mп, доступная телескопу, называется его проницающей силой. Если считать, что dr = 0,6 см, а тс = 0,5, то проникающая сила телескопа (для визуального наблюдения) может быть найдена по формуле



В СССР построен и работает рефлектор с диаметром объектива D = 600 см. Его проницающая сила mп = 20,75; т. е. на 14 единиц звездной величины больше, чем у глаза.

↑ Размен информации

Для удобства сравнения со зрительными трубами мы условно ограничили площадь сетчатки полем зрения 2?'=70°. На такой площади фокусируется изображение, содержащее информацию, максимальное количество которой назовем Н'. Это количество не может увеличиться, как бы мы ни изменяли способ проекции изображения на сетчатку с угловым размером 2?.

Изображению соответствует некоторая картина на местности, которая преобразуется в масштабе Г. При наблюдении невооруженным глазом Г =1 и ? = ?'. При любом увеличении tg ? = (tg ?')/Г [см. формулу (179)]. Таким образом, чем больше увеличение, тем меньше площадь, видимая на местности. Зато эта площадь видна в большем масштабе: на меньшей площади мы сможем различать более мелкие детали, так что общее число деталей остается примерно тем же. Наглядно вариации увеличения можно представить себе так. У нас имеется лист бумаги, на котором изображена карта какой-то местности. Можно взять карту большой площади в малом масштабе или карту небольшой части этой площади, но в большом масштабе. Выбор будет обусловлен тем, что нас интересует: общая ориентировка на местности или подробное научение ее небольшого участка, отыскание малых деталей на нем.

Визуальный оптический прибор не увеличивает количества поступающей в глаз информации. Больше того, из-за неизбежных в приборе аберраций и рассеянного света, снижающего контрасты, количество информации уменьшается. Но зато телескопический прибор может помочь заметить, опознать или детально рассмотреть интересующий наблюдателя объект.

Пусть, например, пастух разыскивает отбившуюся от стада овцу. Если средняя яркость поля 100 кд/м2, а контраст овцы с фоном 0,05, ее можно заметить под углом ?, не меньшим 5,4' [см. формулу (140)]. Приняв, что размер овцы 0,9 м, получим, что увидеть ее можно с расстояния не большего, чем 580 м. Если же пастух воспользуется шестикратным биноклем, эта дистанция возрастет до 3,5 км (правда, действие атмосферы уменьшит это расстояние). Целесообразность применения бинокля в данном случае несомненна. И потеря в количестве информации — как бы плата за ее размен — вполне оправданна.

Более подробное рассмотрение вопроса, насколько полезны могут быть оптические приборы, относится к области прагматических проблем теории информации, определяющих практическую ценность получаемой информации. Эти проблемы еще мало изучены. Поэтому мы ограничиваемся здесь только наглядным примером, приводя случай, когда применение бинокля безусловно полезно.

----

Статья из книги: Глаз и свет | Луизов А.В.