Непосредственное представление видимых поверхностей ? Часть 2

Содержание:
Описание
↑ Допустимые формы представления
До сих пор психофизика всерьез и специально 2,5-мерным эскизом не занималась, и потому нам очень мало известно о нем, причем неизвестно даже, существует ли он на самом деле, в том смысле, как это предполагается в рамках нашего подхода к зрению. Основные вопросы тем не менее сформулировать нетрудно. Что именно представляется и каким образом? Какой именно должна быть система координат (даже сказав, что она должна быть привязана к наблюдателю, Вы оставляете еще много возможностей для выбора)? И возможно, самый трудный вопрос: какого рода обработка информации выполняется в самом представлении - либо для того, чтобы обеспечить его собственную внутреннюю непротиворечивость, либо для того, чтобы обеспечить его совместность с той организацией, допустимость которой определяется трехмерностью структуры реального мира?
Первый вопрос звучит следующим образом: какая именно информация о поверхности воспроизводится в явном виде? Представляются ли, например, и глубина г , и ориентация поверхности s, или в действительности в представление вводится лишь r, а ориентация поверхности определяется при возникновении необходимости с помощью локального дифференцирования? Либо лишь ориентация поверхности представляется в явном виде, а глубина определяется каким-то образом с помощью локального интегрирования? Эту возможность принять значительно труднее, но она определенно отлична от предыдущей.
Наилучший довод в пользу представления в явном виде какой-либо функции типа расстояния от наблюдателя дает теория стереопсиса. Максимальный диапазон значений диспаратности, одновременно поддающихся восприятию без возникновения диплопии, остается одним и тем же в четырех достаточно различающихся случаях. Во-первых, при стабилизации изображения Фендер и Джулес , предъявляя стерео граммы, образованные случайными конфигурациями точек, получали фигуру с размерами порядка 2°. Во-вторых, при отсутствии какой бы то ни было стабилизации (т. е. при нормальных условиях наблюдения) получен приблизительно такой же диапазон. При использовании сложных стереограмм, предложенных Джулесом, и наблюдении с расстояния около 20 см диапазон значений диспаратности имеет приблизительно тот же порядок; если же смотреть на эти стереограммы со значительно более близкого расстояния, то все они оказываются вообще ”не видны”. В-третьих, в настоящее время кажется маловероятным, что максимальный диапазон одновременно воспринимаемых диспаратностей существенно зависит от их распределения. Читатель, воспользовавшись рис. 4.3,
Рис. 4.3. Эксперименты со стереограммами с большими значениями диспаратности. Читатель может попытаться самостоятельно определить наибольшее значение диспаратности при котором он в состоянии одновременно добиться слияния как переднего плана, так и фона. При наблюдении с расстояния 20 см диспаратности этих стереограмм cocтавляют 2° (а), 2,25° (б), 2,5° (в) и 2,75° (г)
может непосредственно убедиться в том, что фигура с размерами порядка 2°, которая воспринимается при стабилизации изображения и при обычных условиях наблюдения стереограмм с непрерывно изменяющимися диспаратностями, сохраняется также и в случае стереограмм с единственной диспаратностью. И, в-четвертых, в условиях ’’любительского” эксперимента, проводимого с помощью собственных пальцев и реальных поверхностей, Вы получите аналогичную фигуру.
Из этих примеров следует, что фигура с размерами порядка 2° для максимального диапазона одновременно воспринимаемых диспаратностей характеризует, очевидно, общий случай (при условии, что имеется достаточно пространства, для крайних значений диспаратности) и что эта фигура не зависит от движения глаз. Трудно понять, каким образом буферное запоминающее устройство, в котором хранится только ориентация поверхности, могло бы реализовывать подобное ограничение, и поэтому я считаю, что значения глубины (быть может, только приближенные значения) в какой-то форме запоминаются, причем значения, которые запоминаются, соответствуют значениям диспаратности порядка 2 — 2,25°.
Вторая группа доводов в пользу явного представления глубины в той или иной форме связана со значением нарушений непрерывности по глубине. Определенные процессы предварительной обработки информации в зрительной системе могут давать информацию о таких нарушениях непрерывности, причем некоторые из них - лишь в качественном виде. Наиболее значительной, вероятно, является роль процессов, связанных с наложением, некоторыми границами на текстурах, границами диспаратности, а также с избирательностью по направлению. О важности субъективных контуров свидетельствует четкость их восприятия. Если глубины расположения двух поверхностей очень сильно различаются, то субъективно мы, по-видимому, прекрасно отдаем себе отчет в этом, несмотря даже на то, что их ориентации абсолютно одинаковы.
Доводы обоих типов указывают на наличие некоторой формы представления глубины. В этой связи возникает одна интересная проблема: соизмерим ли диапазон значений одновременно воспринимаемых глубин в случае видимого движения с возможностями восприятия посредством стереозрения. Ни один из приведенных доводов не предполагает, однако, что информация о глубине должна храниться с высокой точностью, как должно было бы быть в случае формирования первоначального представления. В отдельном случае не составляет труда, опираясь на информацию, полученную при анализе движения или стереопсисе, определять, расположена ли некоторая точка впереди другой точки. Если же, однако, мы попытаемся сравнить расстояния, отделяющие нас от двух поверхностей, которые располагаются в различных частях поля зрения, то хорошего результата мы не получим: человек выполняет такое сравнение значительно менее точно, чем сравнение ориентаций таких поверхностей.
В результате возникают сомнения в том, что глубина является основной представляемой переменной, что ее значения, принадлежащие определенному диапазону, запоминаются точно и что она подвергается дифференцированию при необходимости определить ориентацию поверхности. Кроме того, еще более веские доводы свидетельствуют против такой возможности. Дело в том, что многие из процессов, порождают информацию об ориентации поверхности непосредственно, а не опосредованно — через информацию о глубине. Наиболее очевидными примерами служат процессы, связанные с контурами поверхности, затенением и контурами, характеризующими нарушения непрерывности по ориентации поверхности. В сущности, однако, и стереопсис, и процесс восстановления структуры по движению лучше приспособлены для получения информации о локальных изменениях, чем об абсолютных значениях глубины: стереопсис — в связи с тем, что, по-видимому, мозгу редко бывает известно точное абсолютное значение угла конвергенции глаз и он обычно работает с изменениями этих значений; что касается процесса восстановления структуры по движению, то, поскольку соответствующий анализ проводится локально и предусматривает использование ортогональной проекции, в результате воспроизводятся лишь локальные изменения глубины. Таким образом, существуют серьезные основания считать, что оба указанных процесса очень хорошо приспособлены для получения информации об ориентации поверхности, и, вероятно, правильнее видеть их назначение именно в этом, а не в том, чтобы в первую очередь определять расстояние до наблюдателя.
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
И наконец, ориентация поверхности может определяться очень точно: с точностью до 1—2° во всем диапазоне допустимых ориентаций. Вывод об использовании человеком явного представления ориентации поверхности не основывается целиком на убедительных данных Стивенса, но, учитывая слабые возможности человека по определению глубины, я полагаю, что это — важный факт, и потому, если бы такого представления не существовало, это потребовало бы специального объяснения.
Вывод, который я делаю на основании изложенных доводов, заключается в том, что человек, по-видимому, использует внутреннее представление величины s и r , причем, если величина s может представляться весьма точно, то величина r представляется лишь со значительным приближением. У человека также могут иметься средства для более точного представления локальных различий по глубине, служащих дополнением к используемому человеком представлению ориентации поверхности.
↑ Допустимые системы координат
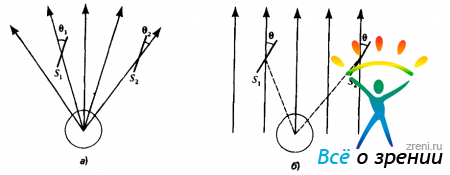
Вероятно, теперь нам следует перейти к проблеме системы координат. Мы уже отмечали, что такая система должна быть ориентирована на наблюдателя, однако и в этом случае еще остается несколько вариантов выбора. Первый и наиболее существенный момент заключается в том, что все обсуждавшиеся нами процессы естественным образом привязаны к координатам сетчатки, как это показано на рис. 4.4, а.
Рис. 4.4. В полярных координатах, привязанных к сетчатке для измерения ориентации поверхности естественно использовать угол, образованный этой поверхностью и линией прямой видимости наблюдателя. Таким образом, двум параллельным поверхностям S1 и S2 соответствуют различные углы ?1 и ?2 с противоположными (в данном случае) знаками (а). Значительно более удобным является представление, которое предусматривает отсчет всех углов от прямой, направленной прямо вверх (б). В таком случае нетрудно определить, параллельны ли две поверхности и являются ли они плоскими, выпуклыми или вогнутыми
Относительная глубина и ориентация поверхности определяются вдоль линии прямой видимости наблюдателя и по отношению к ней, а не относительно какой-либо внешней системы координат. Таким образом, мы чуть ли не форсированно должны считать (по крайней мере сначала), что результаты, приносимые каждым из таких процессов, представляются в некоторой системе координат сетчатки.
Кроме того, следует помнить о том, что координаты, определяемые относительно линии прямой видимости наблюдателя, для него не очень удобны. При использовании такой системы координат нелегко установить, одинакова ли ориентация двух поверхностей или является ли некоторая поверхность плоской. В этом случае все время требуется учитывать угол, под которым располагается линия прямой видимости наблюдателя (как это видно из рис. 4.4, а), причем это осложнение усугубляется влиянием движения глаз.
Второй существенный момент, который следует из первого, состоит в том, что, хотя большая часть процессов предварительной обработки информации в зрительной системе, обеспечивающих получение информации об ориентации поверхности, дает ее применительно к положению линии прямой видимости, каждый процесс может при этом использовать собственный способ. При стереопсисе, как мы видели выше, естественное предпочтение отдается раздельному определению вертикальной и горизонтальной составляющих ориентации поверхности просто из-за того, что горизонтальное расположение глаз обеспечивает разделение вертикального и горизонтального направлений. В процессах, связанных с контурами поверхности и текстурной информацией, предпочтение отдается представлению в категориях отклонение — направление наклона поверхности. С информацией, получаемой в процессе восстановления структуры по движению, в этом отношении дело обстоит, вероятно, аналогично тому, как оно обстоит с информацией, связанной с контурами поверхности.
Итак, в качестве резюме отметим, что существует несколько различных способов представления ориентации поверхности в системе координат сетчатки, причем в различных процессах предварительной обработки информации в зрительной системе могут использоваться несколько отличающиеся друг от друга способы представления первоначальных приближений действительных ориентаций поверхности.
Третий момент определяется наличием у человека центральной ямки сетчатки глаза. Анализ различных частей поля зрения производится при некотором заданном направлении взгляда с очень различным разрешением. Следовательно, в зависимости от того, о какой части зрительного поля идет речь, существенно изменяются объем памяти или размеры зоны буферного запоминающего устройства, необходимые для фиксации результатов функционирования процессов предварительной обработки информации в зрительной системе, причем потребности в памяти в зоне центральной ямки сетчатки оказываются значительно выше, чем в периферийной зоне сетчатки. Таким образом, появляется еще один довод в пользу системы координат сетчатки, поскольку при использовании системы координат, которая учитывала бы и движения глаз, разрешение, соответствующее центральной ямке сетчатки, должно было бы обеспечиваться по всему зрительному полю. Использование таких роскошных ресурсов памяти было бы расточительством — они не являются необходимыми и идут вразрез с нашим собственным опытом восприятия, поскольку в противном случае человек оказался бы в состоянии формировать такое впечатление о внешнем мире, которое было бы повсюду столь же детальным, как и по направлению взгляда.
И наконец, момент, связанный с проблемой непротиворечивости. Мы уже отмечали, что процессы предварительной обработки информации в зрительной системе могут функционировать в значительной степени независимо друг от друга, причем одни части зрительного поля являются областью приложения одних процессов, а другие — других. Следовательно, возникает проблема обеспечения непротиворечивости различных типов информации, а также проблема назначения приоритетов, точно отражающих надежность отдельных процессов, т. е. назначения приоритетов. таким образом, чтобы при получении противоречивой информации из нескольких источников предпочтение отдавалось информации, поступившей из ’’наилучшего” источника. Эта проблема непротиворечивости, как совершенно очевидно, должна быть разрешена на возможно более ранней стадии обработки информации в зрительной системе, поскольку до тех пор, пока она существует, вся получаемая информация не может быть сведена в единственное представление.
Эти четыре замечания ведут к двум выводам. Во-первых, информация, поступающая из различных источников, очевидно, подвергается проверке на непротиворечивость и объединяется с помощью некоторой системы координат сетчатки. Так происходит потому, что вся информация воспроизводится в такой форме, и подобный способ ее представления, учитывающий, помимо всего прочего, повышенную информативность зоны центральной ямки сетчатки,, наилучшим образом соответствует возможностям процессов получения этой информации. Во-вторых, на этом этапе, вероятно, осуществляются определенные преобразования системы координат, целью которых является представление информации, поступающей от различных процессов, в некотором стандартном виде, и, возможно, также учет угла наблюдения. Пример соответствующего преобразования приведен на рис. 4.4, б, где все углы определяются относительно прямой, направленной прямо вперед (от наблюдателя) , а не относительно локальной линии прямой видимости. Подобное преобразование, во-первых, облегчает вычисление предикатов, характеризующих такие свойства, как плоскостность, выпуклость и вогнутость; во-вторых, обеспечивает простоту сравнения ориентаций поверхностей, ’’расположенных” в различных частях поля зрения; в-третьих, открывает возможности для учета движения глаз.
↑ Интерполирование, продолжение и нарушения непрерывности
Проблемы, к обсуждению которых мне хотелось бы перейти, возникают в связи с тремя различными типами психофизических экспериментальных данных. К первому типу относится наблюдение, впервые подробно изученное Уайтом; оно состоит в том, что человек ’’видит” стереограммы, образованные случайными конфигурациями точек, даже при низкой плотности заполнения (2-3 %) как изображения некоторой непрерывной поверхности, а не как набор изолированных точек. У нас создается уверенность в том, что все точки расположены на одной и той же глубине: они явно выделяются на прозрачной во всех остальных отношениях поверхности; эта поверхность - плоская, а ее ориентация ясно видна. Данное явление не будет казаться таким уж удивительным, если вернуться к теории стереопсиса; дело в том, что пересечения нулевого уровня, которым поставлены в соответствие значения диспаратности, покрывают не все изображение - на его большей части пересечений нулевого уровня вообще не имеется. Поэтому следует предполагать, что при этом используется какая-то разновидность процедуры заполнения Отметим, кстати, что кооперативный стереоалгоритм, включает в качестве составной части процесс заполнения, и это было одной из причин его первоначальной привлекательности для нас.
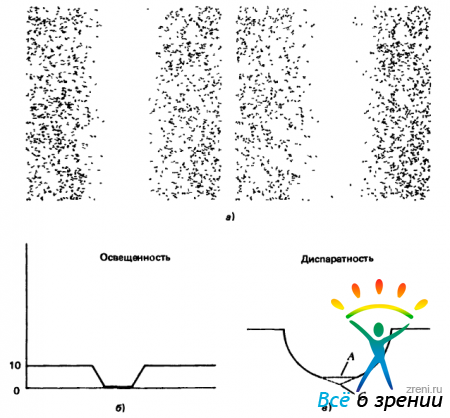
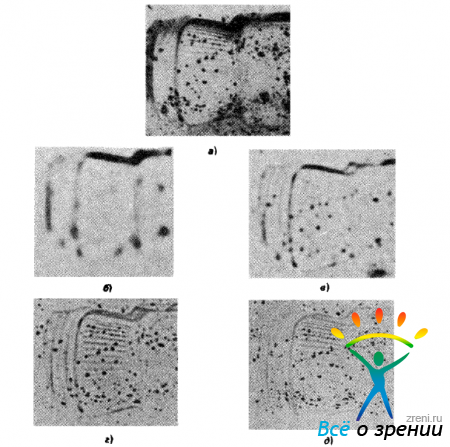
Э. Гримсон рассмотрел заполнение (или задачу интерполирования) в психофизическом и информационном аспектах и обнаружив, что зрительная система оказалась чрезвычайно консервативной в отношении ’’размера” заполнения, выполняемого ею при отсутствии дополнительных данных Он предложил ряд стереограмм (типа приведенной на рис 4.5),
Рис. 4 5. Стереограмма (а) характеризуется распределением плотности размещения точек (б) и распределением значений диспаратности, показанным сплошными линиями (в). Такую стереограмму можно использовать для того, чтобы с психофизических позиций выяснить, прибегает ли человек к интерполированию для заполнения разрывов, и если прибегает, то каким образом он его выполняет? Два допустимых варианта интерполирования показаны штриховыми линиями (в)
в которых и плотность размещения точек, и значения диспаратности уменьшаются по мере приближения к центру, как это показано на рисунке. Вопрос состоит в следующем: каким образом (если это вообще происходит) наблюдатель заполняет область, в которой отсутствуют точки? Два из трех возможных вариантов заполнения приведены на рис. 4.5, в вариант А предусматривает заполнение прямой линией с постоянным значением диспаратности, вариант В (на рисунке не показан) - выполнение некоторого гладкого интерполирования, при котором две поверхности соединяются без нарушения непрерывности по ориентации поверхностей, вариант С - линейное продолжение поверхностей вплоть до их пересечения
Для того чтобы выяснить, что именно воспринимает наблюдатель, следует поместить тестовое пятно в промежуточную область с различными значениями диспаратности и попросить наблюдателя сказать, находится оно выше или ниже того места, ’’где проходит поверхность” Гримсон установил, что при таких условиях восприятие оказывается не очень четким: хотя испытуемые уверенно справляются с вариантами А и С, они проявляют нерешительность относительно положения пятна в варианте В Они никогда не сообщают о каких бы то ни было нарушениях непрерывности по ориентации поверхности. Гримсон пришел к выводу о том, что, хотя, по-видимому, какое-то интерполирование имеет место, проблема в целом не столь проста. Несколько позже мы рассмотрим ее информационные аспекты.
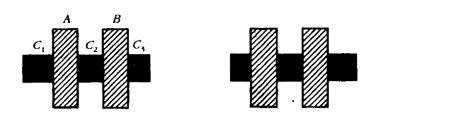
Другой аспект нашей проблемы, который я буду называть продолжением, лучше всего проиллюстрировать с помощью стереопары, предложенной Э. Уиткином и представленной на рис 4.6.
Рис. 4.6. В данной стереопаре область С2 наблюдается на той же самой глубине, что и области и С3, несмотря на отсутствие характеристик диспаратности, позволяющих определять глубину расположения области С2
Эта стереограмма воспринимается как два прямоугольника А и В, наложенных на целостный прямоугольник, включающий части С1, С2 и С3. Любопытной особенностью этого эксперимента служит то, что информацию о стереоскопической диспаратности могут давать лишь вертикальные прямые. Таким образом, области А, В, C1 и С3 содержат точки, в которых значения диспаратности определены, и тот факт, что мы видим каждую из них как отдельную поверхность, относится лишь к проблеме интерполирования. Для области С4, однако, такая информация отсутствует. То, что этой области приписывается та же глубина, что и областям С1 и С3, должно, следовательно, являться результатом какого-то процесса продолжения, действующего ’’позади” наложенных плоскостей А и В. Для данного эксперимента решающее значение имеет точное выравнивание горизонтальных яркостных переходов областей С1, С2 и С3. Это эквивалентно тому, как если бы точное выравнивание этих переходов на двухмерном изображении позволяло наблюдать их в качестве проявления одного и того же нарушения непрерывности поверхности в трехмерном случае, что, в свою очередь, позволяло бы видеть поверхность С2 на той же глубине, что и поверхности С1 и С3. Аналогичный вывод, вероятно, можно сделать, опираясь на эксперименты, поставленные Н. Уайсстайн. Она предъявляла смещающуюся решетку, закрывала ее центральный прямоугольный участок и тем не менее обнаруживала эффекты адаптации даже в пределах этого участка.
Из этих экспериментов следует, что при использовании для представления поверхностей системы координат наблюдателя может возникнуть возможность одновременного представления более чем одной поверхности. Может также оказаться существенным то, что в соответствующим образом построенных стереограммах, образованных случайными конфигурациями точек, возникает возможность одновременно и ясно наблюдать две поверхности. Мне самому не удается видеть одновременно три поверхности, хотя, быть может, есть люди, которые в состоянии сделать это.
И наконец, существует проблема нарушений непрерывности по глубине и ориентации поверхности. Нарушения непрерывности по глубине уже упоминались нами в связи с вариантами продолжения в примере, приведенном на рис. 4.6, а также в связи с явлением возникновения субъективных контуров. В обоих случаях непрерывность и гладкость (минимальная кривизна), по-видимому, являются важными критериями. Уллман с феноменологических позиций провел изучение формы криволинейных субъективных контуров и установил, что ее можно точно представить с помощью двух окружностей (по одной на каждую точку-источник), между которыми должно быть построено гладкое соединение (рис. 4.7).
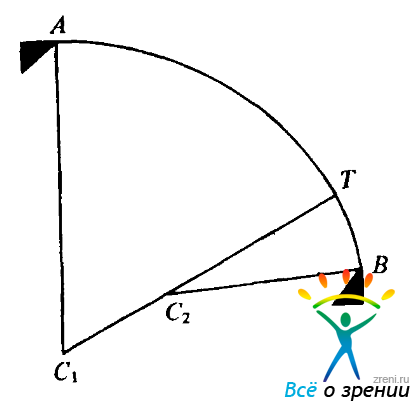
Рис. 4.7. Криволинейный субъективный контур может быть образован двумя окружностями с центрами в точках С1 и С2; каждая из этих окружностей гладко продолжает контур в соответствующей исходной точке (точки А и В), а в точке Г происходит их гладкое соединение. Субъективный контур включает ту из бесконечного множества пар окружностей, которая обеспечивает минимальную кривизну продолжения
Из бесконечного семейства пар окружностей, удовлетворяющих указанному условию, выбирается пара, позволяющая получить минимальную кривизну соединения. Уллман описал также локальную сеть, обеспечивающую порождение формы такого типа.
Хотя форма таких контуров вполне ясна, нам мало известно относительно условий, при которых она возникает, за исключением достаточно общих соображений о необходимости данных о наложении в сочетании с монокулярными данными, более или менее непосредственно характеризующими точное местоположение нарушения непрерывности. Оба эти вида информации в несколько различных вариантах содержатся в треугольнике Канижа, изображении солнца, образованном радиальными прямыми, и стереограмме, образованной случайными конфигурациями точек с 5 %-ным заполнением, в которой собственно ’’точки” содержат короткие вертикальные отрезки яркостных переходов. Эта тема заслуживает дальнейшего исследования с психофизических позиций.
↑ Информационные аспекты проблемы интерплирования
С информационной точки зрения прежде, чем приступать к детальному планированию психофизических экспериментов, необходимо разрешить две проблемы. Первая связана с понятием нарушения непрерывности, а вторая - с различными вариантами интерполирования.
Нарушения непрерывности
Хотя различия между непрерывными и разрывными изменениями на континууме очевидны, в тех случаях, когда выборочное пространство дискретно, эти различия становятся трудноуловимыми. Мы уже дважды сталкивались с этой проблемой - первый раз при обнаружении нарушений непрерывности по ориентации пересечений нулевого уровня, т. е. когда, строго говоря, такие нарушения возникать не могут, и второй раз в связи с алгоритмом светлоты Ланда и Макканна. В обоих случаях предусмотрено введение некоторой пороговой величины. В первом случае в качестве основы для него используется та точка, в которой ’’реальное” нарушение непрерывности (источник) перестает быть различимым с очень резким изменением кривизны. Положение этой точки зависит от размера рецептивного поля соответствующего канала; в результате то, что каналы с рецептивными полями меньших размеров могут ’’воспринимать” как гладкость, каналы с рецептивными полями больших размеров могут ’’воспринимать” как нарушения непрерывности.
Разрешение выборочного пространства в любом случае действительно налагает ограничения на то, что можно считать непрерывным изменением. Допустим, например, что в одномерном случае исходное представление включает значения, разделенные некоторыми промежутками б. В таком случае согласно теореме Котельникова - Шеннона данное представление не может включать полную информацию о процессах, частота которых превышает, скажем, ?/? = ?. Следовательно, это представление в частотной области, в сущности, ограничено частотой ?.
Далее, хотя сигнал, полоса частот которого ограничена сверху частотой ?, можно точно представить его выборочными значениями, разделенными промежутками ?, это никак не гарантирует того, что такой сигнал будет соответствовать всем выборочным точкам, в которых будут заданы произвольные значения. Иначе говоря, если выборочные значения изменяются слишком быстро, сигнал в целом может выйти за пределы ширины полосы частот, используемой для его представления. При возникновении такой ситуации представление автоматически приписывает соответствующее изменение нарушению непрерывности просто потому, что не располагает возможностями, необходимыми для учета тех изменений, которые имеют место на самом деле. Это обстоятельство точно отражается в теореме Бернштейна, утверждающей, что производная функции с ограниченным спектром не может принимать слишком большие по сравнению со значением самой функции значения. Если f(х) — некоторая функция, полоса частот которой ограничена сверху частотой ?, a f'(x) - ее производная, то теорема утверждает, что
sup ? f '(x) ? ? ? sup ? f(x) ?,
т. e. максимальное значение модуля производной ? f '(x) ? при любых значениях х не превышает максимального значения ? ? f(x) ?.
Это — фундаментальное ограничение; оно действует во всех тех случаях, когда предпринимается попытка представлять некоторую информацию дискретно (на дискретной решетке). В связи с этим особенно примечательно то, что зрительная система человека не в состоянии представлять синусоидальные сигналы с учетом их глубины, если частота таких сигналов превышает 3-4 периодов/град в центральной ямке сетчатки. Это ограничение, возможно, помогает понять, почему субъективные контуры не возникают или видны не очень отчетливо, если Вы смотрите на них прямо, и видны значительно более отчетливо, когда Вы смотрите на них не прямо. Возможно также, что разрешающая способность представления уменьшается с увеличением эксцентриситета; таким образом, то, что допускает представление в центральной ямке сетчатки как очень высокий градиент, при предъявлении с большим эксцентриситетом должно представляться как некоторое нарушение непрерывности.
Cтереопсис иногда может давать вполне определенные данные о нарушении непрерывности поверхности. Если, например, относительное значение изменения диспаратности по горизонтали в одном из глаз достигает 1, то другой глаз в этом случае воспринимает нарушение непрерывности по глубине. Слабо заполненные изображения, однако, часто не содержат информации, достаточной даже для того, чтобы установить этот факт. При восприятии у Вас может возникнуть не очень определенное ощущение того, что диспаратность действительно изменяется, но Вы не можете точно сказать, где именно. Если при предъявлении стереограмм, образованных случайными конфигурациями точек со слабым заполнением, оказывается, что два квадрата располагаются вдоль границы диспаратности, то возникают отчетливые субъективные контуры и граница ясно видна. Если же, однако, в стереограмме квадраты заменены, например, размытыми пятнами, то восприятие нарушения непрерывности становится значительно менее определенным.
Хотя все эти наблюдения не выходят далеко за пределы чистых гипотез, они действительно служат свидетельствами консервативности процесса интерполирования, а также и того, что зрительная система весьма неохотно вводит контуры нарушений непрерывности как по глубине, так и по ориентации поверхности, за исключением тех случаев, когда само изображение оказывается источником достаточно объективной информации об их расположении. Контур может проявляться не по всей своей длине, но маловероятно, чтобы по всей его длине совершенно отсутствовали всякие зрительно воспринимаемые проявления его существования. Э. Гримсон сформулировал это положение в виде следующего афоризма: позиции, в которых нет информации, - это на самом деле позиции, в которых информация есть. Другими словами, нарушения непрерывности скрыть невозможно, и справедливо также и обратное: если изображение не дает вообще никаких данных относительно наличия какого-либо нарушения непрерывности, причем на тех участках, где можно было предполагать существование яркостного перехода, отсутствует даже хотя бы один его фрагмент, то в таком случае можно не постулировать наличие нарушения непрерывности Таким образом, в тех ситуациях, когда непосредственные признаки намеренно устранены, как это сделано на рис. 4.5, мы не можем с полной определенностью ни вводить контуры, ни интерполировать поверхности и, следовательно, результат восприятия, с которым мы остаемся, отличается зыбкостью и неопределенностью
Методы интерполирования
Упоминания заслуживают три основных метода интерполирования: 1) линейное интерполирование глубины r ; 2) линейное интерполирование ориентации поверхности; 3) интерполирование методом ’’обтекаемой поверхности” (этот метод используется при конструировании автомобилей для придания кузову гладкой формы). Очень приблизительно первый метод аналогичен тому обратному преобразованию, с которым мы уже встречались в предложенном Хорном алгоритме ретинекса. Этот метод предусматривает минимизацию значения оператора Лапласа ?2 на соответствующей поверхности. Второй метод предусматривает приближенную минимизацию кривизны поверхности в любой заданной вогнутой или выпуклой области. (Это следует из того, что кривизна J = - div n, где div n - дивергенция n; n - нормаль к поверхности, и локальное усреднение n практически обеспечивает минимизацию значения div n.) Недостатком обоих методов в случае реализации их на некоторой решетке является медленная сходимость — в сущности, ее скорость обратно пропорциональна квадрату расстояния между узлами решетки. Мне уже доводилось выше высказывать свои сомнения относительно использования итерационных методов при обработке информации, связанной с восприятием.
Третий метод интерполирования, который Гримсон предпочитает двум первым, основан на использовании понятия обтекаемой поверхности, т. е. поверхности с непрерывными первой и второй производственными, а в производных третьего и высшего порядков допускающей разрывы. Известны методы, обеспечивающие в результате однократного применения заполнение промежутков между тремя соседними точками и связывание разрывных мест таким образом, чтобы обеспечивалась гладкость производных произвольного высшего порядка. Отказ от условия непрерывности для производных выше второго порядка основан на наблюдениях специалистов по автомобильному дизайну, сводящихся к тому, что покупатель замечает нарушение непрерывности формы поверхности лишь по первой и второй производным, а на третью уже не обращает внимания. На рис 4.8
Рис. 4.8. (окончание)
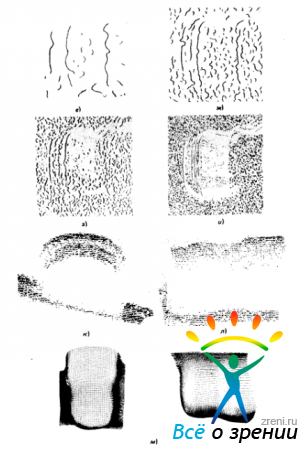
Рис. 4.8. Изображение, порожденное стереопарой (а); результаты его свертки с ?2 G-фильтрами с рецептивными полями четырех различных размеров (б—д соответственно) ; картины пересечений нулевого уровня, полученные в результате указанной фильтрации (е-и); две проекции карты диспаратностей, полученные в результате установления соответствий между изображениями стереопары (к, л); изображения поверхностей, полученные в результате применения к этой информации алгоритма интерполирования, предложенного Э. Гримсоном (м, н)
приведены результаты применения одного из методов заполнения такого рода к изображению, порожденному стереопарой Из этого примера следует, что метод позволяет получать гладкое изображение, которое радует глаз.
Что же касается проблем соотношения этих рассуждений информационного характера с тем, каким образом человек на самом деле обнаруживает нарушения непрерывности или заполняет разрывы поверхностей (в том ограниченном диапазоне возможностей выполнения этих операций, которыми он обладает), то их разрешение - дело будущего.
↑ Другие информационные процессы, действующие в рамках 2,5-мерного эскиза
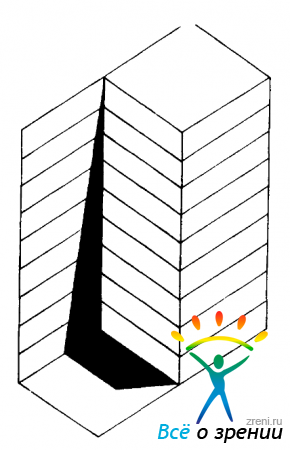
Понятие непрерывности поверхности может, как мы уже в этом убедились, послужить источником разнообразных процессов обработки информации, действующих в рамках 2,5-мерного эскиза, в том числе процессов заполнения разрывов и гладкого продолжения, применяемых к нарушениям непрерывности. Можно полагать, что в таких процессах подобным же образом учитываются и иные локальные ограничения, например условия непротиворечивости, определяющие допустимое расположение поверхностей друг относительно друга в трехмерном пространстве, типа условий, сформулированных в явном виде Уолцем. Подобные ограничения в конечном счете могут послужить основой для понимания таких явлений, как трансформация куба Некера. Исходя из такой точки зрения естественным выглядит возникновение в результате стереоскопического слияния многих иллюзий, связанных с интерпретацией трехмерной структуры (куб Некера, субъективные контуры, иллюзия Мюллера — Лайера, иллюзия Поггендорфа и т. п.). Иллюзии типа ’’перевернутое ведро” также частично возникают в силу этих же причин, поскольку непрерывность поверхности ведра играет решающую роль в том, чтобы оно воспринималось должным образом. В связи с этим возникают интересные вопросы: какой объем обработки приходится на операции, выполняемые в самом 2,5-мерном эскизе, и какой ее объем приходится на этап преобразования этого промежуточного представления в трехмерное представление того типа, которое человек сохраняет в памяти? Такие иллюзии, как треугольник Пенроуза, целый ряд изображений, созданных Эшером, и даже трансформирующаяся фигура, изображенная на рис. 4.9,
Рис. 4.9. Странные трансформации этой фигуры, возможно, как и трансформации куба Некера, определяются ограничениями, включенными в 2,5-мерный эскиз
служат, вероятно, примерами проявления совместного воздействия нескольких эффектов — частично локальных, относящихся к 2,5-мерному эскизу, а также других, возникающих в связи с тем, что по набору локальных проекций не удается построить целостную непротиворечивую трехмерную интерпретацию.
И наконец, еще одно замечание, которое может показаться странным. Почему должны происходить трансформации куба Некера при включении его в стереограмму, образованную случайными конфигурациями точек? Можно было бы сказать, что поскольку стереопсис однозначно приписывает все яркостные переходы некоторой плоскости, то соответствующая фигура должна восприниматься, как двухмерная, а не трехмерная. Я полагаю, что лучше всего считать все контуры 2,5-мерного эскиза с трудом поддающимися трехмерной интерпретации. Не имеет значения то обстоятельство, что включены они в 2,5-мерный эскиз по результатам процесса стереопсиса, а не заимствованы, например, из первоначального эскиза.
----
Статья из книги: Зрение | Д. Марр



Комментариев 0