Определение точек пересечения сигналом нулевого уровня и исходный первоначальный эскиз

Содержание:
Описание
↑ Определение точек пересечения сигналом нулевого уровня
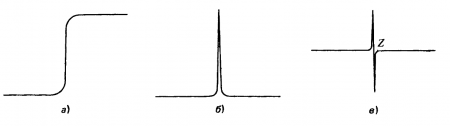
Первый из описанных выше трех этапов посвящен обнаружению изменений яркости. Основу этого процесса составляют два следующих положения: 1) поскольку изменения яркости изображения могут относиться к различным масштабным уровням, для того, чтобы оптимизировать процесс их обнаружения, необходимо применять операторы, обрабатывающие фрагменты изображения различных размеров; 2) резкое изменение яркости приводит к возникновению пика или впадины первой производной, что эквивалентно пересечению нулевого уровня второй производной, как это показано на рис. 2.8
Рис. 2 8. Иллюстрация понятия ’’пересечение нулевого уровня”. Изменение яркости (а) порождает пик в первой производной (б) и (резкое) пересечение нулевого уровня во второй производной (в)
(пересечением сигналом нулевого уровня называется та точка, в которой соответствующая функция меняет свое значение с положительного на отрицательное).
Из этого следует, что для эффективного обнаружения изменения яркости необходимо пользоваться фильтром, обладающим двумя существенными свойствами. Прежде всего он должен реализовывать некоторый дифференциальный оператор, вычисляющий первую или вторую пространственную производную изображения. Кроме этого он должен допускать настройку на работу на необходимом масштабном уровне с тем, чтобы фильтры, предназначенные для обработки больших фрагментов изображения, можно было использовать для обнаружения границ на размытых затемненных участках изображения, а фильтры, предназначенные для обработки малых фрагментов изображения, — для обнаружения малых элементов изображения на его хорошо сфокусированных участках.
Марр и Хилдрет показали, что в наибольшей степени этим требованиям соответствует ?2 G-фильтр, где ?2- оператор Лапласа (?2/?х2 +?2/?у2), а символ G обозначает распределение Гаусса
со средним квадратическим отклонением а. График оператора ?2 характеризуется круговой симметрией и имеет форму сомбреро; двухмерное распределение значений этого оператора можно задать через расстояние г от начала координат с помощью следующего выражения:
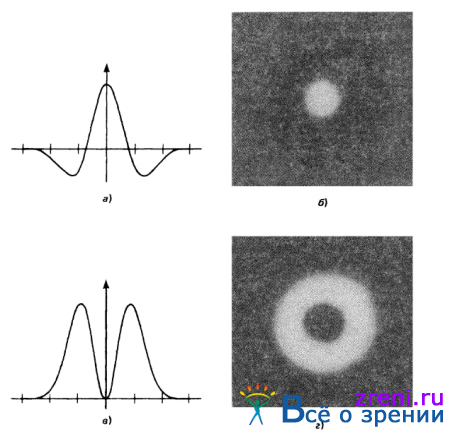
На рис. 2.9
Рис. 2.9. Представление ?2 G-фильтра в виде одномерной (в) и двухмерной (б) функций (значения этих функций соответствуют яркости в каждой точке) и фурье-преобразования одномерного (в) и двухмерного (г) вариантов соответственно
представлены одномерный и двухмерный варианты этого оператора, а также их фурье-преобразования.
Выбор фильтра типа ?2 G определяется в основном двумя моментами. Во-первых, за счет гауссовской части G изображение размыто, на нем эффективно уничтожены все структуры, относящиеся к масштабному уровню, существенно меньшему значения пространственной постоянной ? гауссовского распределения. В качестве соответствующего примера на рис. 2.10
Рис. 2.10. Размывание изображений составляет первый этап обнаружения на них изменений яркости. Поскольку на исходном изображении (а) изменения яркости могут отмечаться на значительном числе масштабных уровней, ни один оператор в отдельности не обеспечит выделения всех этих изменений с высокой эффективностью. Эта задача существенно упрощается, если изображение размыто с помощью гауссовского фильтра, поскольку при этом, в сущности, сверху ограничивается допустимый темп изменений яркости. Первый этап процесса обнаружения границы можно рассматривать как разбиение исходного изображения на ряд копий, к каждой из которых применяется гауссовский фильтр, предназначенный для обработки фрагментов определенного (своего для каждого фильтра) размера; соответственно изменения яркости определяются для каждой копии изображения отдельно. Изображение (б) обработано гауссовским фильтром, имеющим а, равную 8 пикселам. Изображение (в) обработано гауссовским фильтром, имеющим а, равную 4 пикселам. Размер изображения 320X320 пикселов
представлено изображение, подвергнутое свертке с помощью двух гауссовских фильтров, предназначенных для работы на разных масштабных уровнях. У одного из них пространственная постоянная ? равна 8 пикселам (рис. 2.10, б), у другого — 4 пикселам (рис. 2.10, в). Причина выбора в данном случае для размывания изображения гауссовского фильтра, а не, скажем, оператора, график которого имеет вид цилиндрической женской шляпы без полей и с плоским донышком, заключается в том, что гауссовское распределение обладает необходимыми свойствами — оно гладко и локализовано как в пространственной, так и в частотной области и, строго говоря, представляет собой единственное распределение, характеризующееся одновременно оптимальной локализацией в обеих областях. Такие свойства функции размывания, в свою очередь, желательны потому, что при максимально возможной равномерности размывания как в пространственной, так и в частотной области вероятность внесения каких-либо изменений, отсутствующих на исходном изображении, оказывается минимальной.
Второй момент касается дифференцирующей части фильтра ?2.Важнейшее преимущество, которое обеспечивается благодаря ее использованию, — экономичность вычислительной процедуры. Можно взять производные по направлению первого порядка типа ?/?х или ?/?у, что влечет за собой необходимость отыскивать их локальные максимумы или минимумы по каждой из направлений (как это показано на рис. 2.8,6), либо производные по направлению второго порядка типа ?2/?х2 или ?2/?у2 — в этом случае изменения яркости изображения будут соответствовать тем точкам, в которых они принимают нулевые значения (см. рис. 2.8, в). Все эти операторы, однако, обладают тем недостатком, что они являются направленными — применение любого из них связано с учетом ориентации нескольких дифференциальных операторов первого и второго порядков (см. рис. 2.11,
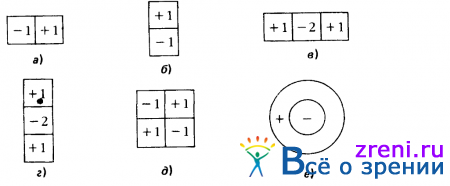
Рис. 2.11. Пространственная организация дифференциальных операторов низших порядков. Операторы типа ?/?х допускают приближенную реализацию с помощью фильтров, рецептивные поля которых имеют вид, представленный на рисунке: а, б — операция ?/?х, рассматриваемая как измерение разности значений яркости в двух соседних по оси х точках; в — операция ?2/?х2, рассматриваемая как процедура определения разности двух соседних значений ?/?х, т. е. рецептивного поля; г, д — рецептивные поля двух других операторов второго порядка ? и ?2/дхду соответственно; е — рецептивное поле изотропного оператора самого низшего порядка (оператора Лапласа (?2/?х2 + ?2/?у2) , для которого используется обозначение ?2 ), характеризуется круговой симметрией
иллюстрирующий пространственную организацию, т. е. ’’рецептивное поле” на нейрофизиологическом языке). Использование первых производных требует, в частности, определения значений ?I/?х и ?I/?у и отыскания локальных максимумов и минимумов амплитуды их суммарных значений, т. е. определения также и знака, и значения величины
Применение операторов, реализующих вычисление производных второго порядка по направлению, порождает проблемы еще более неприятные, чем те, которые возникают в связи с производными первого порядка. Единственный способ избежать подобных дополнительных вычислительных затрат — это попытаться применить оператор, не зависящий от направления. Изотропным дифференциальным оператором самого низшего порядка является лапласиан ?2, и, как оказалось, этот оператор можно использовать для обнаружения изменений яркости изображения, если размытое изображение удовлетворяет нескольким чрезвычайно слабым ограничениям. Изображения, как правило, локально удовлетворяют таким ограничениям, и поэтому при решении реальных задач допустимо пользоваться оператором Лапласа. Итак, практически наиболее удовлетворительный способ отыскания на изображении изменений яркости, относящихся к некоторому определенному масштабному уровню, заключается в предварительной фильтрации изображения с помощью оператора ?2 G, пространственная постоянная части G которого выбирается таким образом, чтобы был обеспечен учет того масштабного уровня, к которому относятся искомые изменения яркости, после чего на изображении, полученном в результате фильтрации, отыскиваются точки пересечения нулевого уровня.
На рис. 2.12 — 2.14
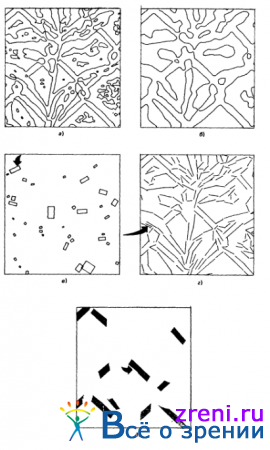
Рис. 2.12, 2.13, 2.14. Примеры, иллюстрирующие обнаружение точек пересечения нулевого уровня с помощью оператора ?2 G: а — изображение размера 320X320 пикселов; б — результат свертки этого изображения с помощью оператора ? 2 G при w2—D = 8(нулевые значения представлены серым цветом) ; в — положительные (белый цвет) и отрицательные (черный цвет) значения; г — только пересечения нулевого уровня
показано, как выглядит изображение, подвергнутое такой обработке. Цифровые значения элементов изображения, полученного в результате фильтрации с помощью оператора ?2G, могут быть как положительными, так и отрицательными, но суммарное среднее значение равно нулю. Положительным значениям на этих рисунках соответствует белый цвет, отрицательным — черный, а нулевым — некоторый промежуточный уровень серого тона. Как уже отмечалось, существенным свойством оператора ?2G является то, что точки, в которых график его значений пересекает нулевой уровень, служат индикаторами изменений яркости на изображении, размытом с помощью гауссовской функции распределения с некоторой пространственной постоянной. На приведенных рисунках это прекрасно видно. Так, на рис. 2.12, в представлено изображение, которое после фильтрации было подвергнуто ’’бинаризации”, т. е. всем его элементам с положительными значениями были присвоены значения ”+1”, а элементам с отрицательными значениями —
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
значения ”—1” На рис. 2.12, г изображены лишь точки пересечения нулевого уровня. Преимущество бинаризованного представления заключается также в том, что оно указывает знак пересечения нулевого уровня, т. е. позволяет судить о том, какая сторона изображения темнее.
Кроме того, угол, под которым происходит пересечение нулевого уровня, зависит, хотя и не непосредственно, от степени изменения яркости. Это обстоятельство иллюстрируется рис 2.15,
Рис. 2.15. Иллюстрация представления пересечений нулевого уровня. Яркость линий изменяется в соответствии со значением угла пересечения нулевого уровня, что позволяет легче понять, какие линии представляют наиболее контрастные участки изображения
на котором представлено исходное изображение с нанесенными на нем точками пересечения нулевого уровня, последние соединены кривыми различной яркости. Кривая тем контрастнее, чем больше угол, под которым происходит пересечение нулевого уровня (измеряется относительно перпендикуляра к направлению сигнала в соответствующей точке)
Для формализации представления точек пересечения нулевого уровня типа воспроизводимых на рис. 2.12 — 2.15 можно воспользоваться несколькими различными способами. Для их представления мы будем пользоваться набором направленных непроизводных элементов, называемых отрезками пересечений нулевого уровня. Каждый из таких непроизводных элементов служит описанием некоторой части контура, у которой крутизна яркости (скорость изменения значения свертки на отрезке) и локальное направление остаются приблизительно одинаковыми. В связи с тем, что это в конечном счете оказывается существенным с физической точки зрения, необходимо выделить те точки, в которых направление пересечений нулевого уровня меняется ’’разрывно”. Кавычки в данном случае необходимы, поскольку на самом деле можно доказать, что изменение направления пересечений нулевого уровня графиком свертки ?2G *I ни при каких обстоятельствах не имеет разрывов,однако, тем не менее, удается сформулировать определение разрывности, пригодное для использования. Кроме того, небольшие замкнутые контуры представляются пятнышками, каждое из которых также характеризуется ориентацией, средней крутизной яркости и размерами, определяемыми их протяженностями вдоль большой и малой осей. И наконец, в соответствии с глобальной целью, для того чтобы обеспечить обнаружение изменений яркости в полном диапазоне всех тех масштабных уровней, на которых они возникают на изображении, необходимо использовать операторы, предназначенные для обработки фрагментов изображения нескольких различных размеров.
↑ Биологические следствия
Эта вычислительная схема, характеризующая самые первые этапы обработки зрительной информации, позволяет интерпретировать большое число результатов, полученных в процессе психофизических и нейрофизиологических исследований нижнего уровня зрения, а также может быть источником гипотез относительно общих принципов организации начальной части зрительного пути.
Психофизика нижнего уровня зрения
В 1968 году Кампбелл и Робсон поставили несколько экспериментов по зрительной адаптации. Они обнаружили, что контрастная чувствительность испытуемых временно понижается после предъявления им высококонтрастных решеток, причем это понижение зависит от ориентации и пространственной частоты решетки. В результате экспериментаторы пришли к выводу, что зрительный путь содержит некоторый набор ’’каналов”, обладающих избирательностью по ориентации и пространственной частоте.
Это открытие породило подлинный взрыв в области исследования отдельных подробностей структуры этих каналов, кульминацией которых явилась предложенная не так уж давно элегантная количественная модель структуры таких каналов, имеющейся у человека. В основу этой модели были положены данные порогового обнаружения, полученные Уилсоном и Гисом и Уилсоном и Бергеном. Понять эту модель очень легко. Идея, положенная в ее основу, состоит в том, что в каждой точке поля зрения размещаются четыре настраиваемых на пространственный размер фильтра (маски), предназначенные для анализа изображения. Пространственные поля каждого из этих фильтров имеют форму, приблизительно соответствующую разности двух гауссовских распределений (РГР), однако два фильтра, реализующие маски меньших размеров, проявляют в основном тонические временные свойства, а два фильтра, реализующие маски больших размеров, - в основном фазные. Размер маски, соответствующей каналу, растет линейно в соответствии с увеличением эксцентриситета (углового расстояния от центральной ямки сетчатки глаза); каналы обозначаются символами N, S, Т и U в порядке увеличения размера маски. Канал S обладает наибольшей чувствительностью как по отношению к тонической, так и фазной стимуляции; канал же U отличается наименьшей чувствительностью, составляющей всего лишь от одной четвертой до одной одиннадцатой чувствительности канала S. Сам Уилсон не выдвигал никаких утверждений относительно направленности фильтров, но он определил их размеры, используя светлые и темные линии. При использовании таких одномерных раздражителей ширина центральной части рецептивного поля (мы будем обозначать ее символом w1-D) имеет следующие значения: 3,1' (канал N; 6,2' (канал S); 11,7' (канал Т); 21' (канал U). Размеры рецептивного поля растут линейно с увеличением эксцентриситета (приблизительно вдвое при эксцентриситете, равном 4° ). Фактически все психофизические данные, относящиеся к обнаружению пространственных образов, которые .характеризуются порогом различимости менее 16 периодов на градус, допускают интерпретацию в рамках этой модели в сочетании с гипотезой, предполагающей, что в основе процесса обнаружения лежит некая разновидность пространственной вероятностной суммации, осуществляемой в указанных каналах.
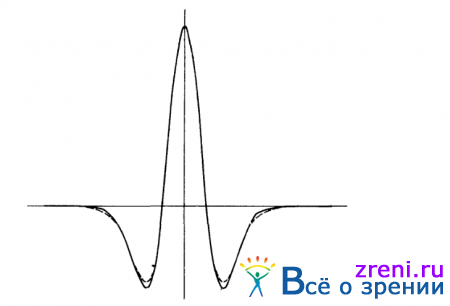
Как я считаю, именно ?2 G-фильтры составляют основу каналов, существование которых подтверждается психофизическими данными. Оператор ?2 G аппроксимирует некоторый полосовой фильтр с полосой пропускания в 1,25 октавы, соответствующей половине энергии спектра. Такой фильтр можно приближенно представить с помощью РГР, причем наилучшее - с технической точки зрения - приближение достигается в тех случаях, когда пространственные постоянные двух гауссовских распределений, образующих РГР, характеризуются отношением 1:1.6. Рисунок 2.16
Рис. 2.16. Наилучшая с технический точки зрения реализация ?2G-фильтра (сплошная линия) с помощью разности двух гауссовских распределений (РГР), достигаемая при соотношении тормозной и возбуждающей пространственных постоянных, равном приблизительно 1:1,6. РГР представлена на этом рисунке штриховой линией. Обе кривые имеют очень похожие профили
характеризует качество подобной аппроксимации. Оценка Уилсона этого отношения для тонических каналов составляет 1:1,75.
Для того чтобы использовать найденные Уилсоном и Бергеном числовые значения величины W1-D при определении диаметра центральных частей рецептивных полей соответствующих операторов ?2 G, необходимо умножить значения первых на ?2, поскольку измерения Уилсона соответствуют линейной проекции рецептивных полей с круговой симметрией. Таким образом, канал N Уилсона соответствует некоторому ?2 G-фильтру, диаметр центральной части рецептивного поля которого W2—D =3,1?2=4,38', что примерно соответствует девяти колбочкам центральной ямки сетчатки глаза. Это значение кажется слишком большим для наименьшего из каналов, и доводы, основанные на теоретическом анализе остроты и разрешающей способности зрения, указывают на существование еще меньшего канала. Диаметр w2-D центральной части рецептивного поля такого канала должен составлять около 1'20", и из-за дифракции в глазу речь может идти о карликовых ганглиозных клетках, центральные части рецептивных полей которых состоят лишь из одной колбочки.
Итак, если считать числовые оценки Уилсона правильными, то они позволяют судить о том, какими размерами исходные операторы типа ’’центр-периферическое кольцо” должны обладать, для того чтобы обеспечивать возникновение наблюдаемой психофизической адаптации и других феноменов. Вообще говоря, эти цифры можно было бы соотнести с результатами физиологических измерений, и в следующем разделе мы укажем соответствующий способ. И наконец, в этой связи следует отметить, что Кампбелл обнаружил также зависимость адаптации от ориентации (она, кроме того, может зависеть и от направления движения). Эту особенность мы связываем с этапом обнаружения пересечений нулевого уровня, который лучше всего рассматривать на нейрофизиологическом уровне.
Физиологическая реализация ?2 G-фильтров
С момента появления работы Каффлера известно, что пространственная организация рецептивных полей ганглиозных клеток сетчатки характеризуется круговой симметрией, причем их центральная часть выполняет возбуждающие функции, а периферическая - тормозящие. Некоторые клетки (их называют клетками, реагирующими на появление светлого раздражителя в центре рецептивного поля (КСЦР)) возбуждаются при появлении в центре их рецептивного поля небольшого светлого пятна, а остальные при этом затормаживаются. Родик и Стон высказали предположение, согласно которому такая организация является результатом наложения небольшой центральной области возбуждения на значительно больший тормозящий ’’купол”, простирающийся над всем рецептивным полем. Инрот - Кугелл и Робсон представили два таких купола гауссовскими распределениями, получив в результате описание рецептивного поля как некоторой разности двух гауссовских распределений. Кроме того, Инрот - Кугелл и Робсон исходя из временных характеристик их реакции на стимуляцию разделили большие ганглиозные клетки сетчатки на два класса — X и Y. Первые демонстрируют явно выраженную тоническую реакцию, а вторые - в основном фазическую, причем это различие сохраняется и на уровне клеток наружного коленчатого тела. Вероятно, тонические каналы Уилсона соответствуют на физиологическом уровне X-клеткам, а фазные каналы — Y-клеткам.
Таким образом, не столь уж беспочвенным является предположение о том, что X-клетки сетчатки и наружного коленчатого тела воспроизводят именно значения функции ?2 G, причем положительные значения воспроизводятся клетками КСЦР, а отрицательные — клетками, реагирующими на появление темного раздражителя в центре рецептивного поля (КТЦР). Для иллюстрации физиологических аспектов этого механизма на рис. 2.17
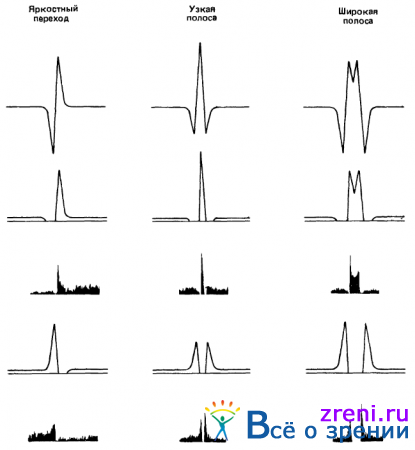
Рис. 2.17. Сопоставление предсказанных ответов X-клеток КСЦР и КТЦР с результатами электрофизиологических исследований. В первом ряду представлены значения ?2 G *I для изолированного яркостного перехода тонкой полосы (ширина полосы составляет 0,5 w 1-D, где w 1-D- значение ширины центральной возбуждающей части рецептивного поля, спроецированной на некоторую прямую) и толстой полосы (ширина полосы составляет 2,5w1_D). Теоретический прогноз был получен с помощью наложения положительных (второй ряд) или отрицательных (четвертый ряд) частей графика ?2 G *I на график фоновой активности клетки, значения которой невелики (ответ клетки в невозбужденном состоянии). Соответствующие физиологические данные (третий и пятый ряды) заимствованы из (ответы на предъявление края) и (ответы на предъявление полос шириной 1 и 5°)
сопоставляются ответы X-клеток, предсказанные с помощью функции ?2 G, и опубликованные в научной литературе значения ответов клеток сетчатки и наружного коленчатого тела, идентифицированных нами в качестве X-клеток, для раздражителей трех видов — яркостного перехода, узкой и широкой полос. Очевидно, что имеет место очень точное качественное совпадение соответствующих результатов.
Физиологический механизм обнаружения пересечений нулевого уровня
С физиологической точки зрения отрезки пересечений нулевого уровня легко выделяются независимо от обнаружения точек пересечения нулевого уровня, ибо выделение таких отрезков на основе обнаружения точек пересечения нулевого уровня — неправдоподобная в физиологическом смысле идея. Причина этого заключается в том, что по одну сторону непосредственно от точки пересечения нулевого уровня располагается положительный локальный максимум изображения, полученного в результате фильтрации ( ? 2 G * I), а непосредственно по другую - отрицательный. Расстояние между этими локальными максимумами составляет примерно W2 -D/?2, где w2 —D - ширина центральной части рецептивного поля соответствующего ?2 G-фильтра. Следовательно, непосредственно по одну сторону от точки пересечения нулевого уровня наблюдается интенсивный разряд клетки КСЦР и непосредственно по другую — интенсивный разряд клетки КСЦР. Сумма значений ответов этих клеток соответствует углу, под которым происходит пересечение нулевого уровня - высококонтрастные изменения яркости порождают более интенсивный разряд, чем низкоконтрастные. Таким образом, пересечение нулевого уровня может быть обнаружено с помощью какого-либо механизма, обеспечивающего соединение клетки КСЦР и клетки КТЦР с логическим элементом И, как это показано на рис. 2.18, а.
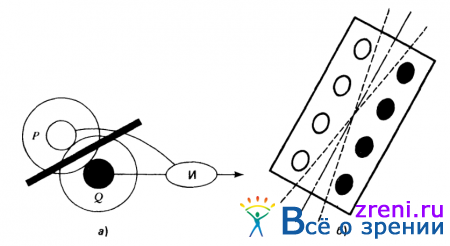
Рис. 2.18. Механизм обнаружения ориентированных отрезков пересечения нулевого уровня. На рис. 2.18, а Р-рецептивное поле Х-клетки КСЦР наружного коленчатого тела, Q -рецептивное поле Х-клетки КТЦР наружного коленчатого тела. При возбуждении обеих клеток между ними должно происходить пересечение нулевого уровня. Следовательно, если эти клетки, как показано на рисунке, соединены с логическим элементом И, последнее обеспечит обнаружение наличия пересечения нулевого уровня. Если имеется набор пар таких клеток (б), причем каждая пара также соединена со своим логическим элементом И, то полученное в результате устройство будет обеспечивать обнаружение ориентированного отрезка пересечений нулевого уровня, расположенного в пределах границ, указанных приближенно штриховой линией. Идеальным случаем было бы использование логических элементов, воспроизводящих результат суммирования лишь при возбуждении всех его Р- и Q-входов
Эту идею несложно использовать и для обнаружения направленности отрезка пересечения нулевого уровня: необходимо просто расположить X-клетки КСЦР и КТЦР в два столбца, как это показано на рис. 2.18, б. Если связать все эти элементы с логическими элементами И или другими устройствами, обеспечивающими достаточно хорошее приближение их функции, то в результате возникнет устройство, обеспечивающее обнаружение отрезка пересечений нулевого уровня, ориентация которого ограничена двумя штриховыми линиями, изображенными на рис. 2.18, б. Эта идея составляет основу для синтеза модели простых клеток зрительной коры. Сейчас же достаточно заметить, что подобные устройства способны реагировать на ориентацию и настраиваться на пространственную частоту. Как я полагаю, адаптивность именно этих элементов обнаружили Кампбелл и Робсон в своих экспериментах в 1968 году.
Первое полностью формализованное представление изображения
Использование точек пересечения нулевого уровня является естественным способом перехода от аналогового (непрерывного) представления, например задаваемого значениями яркостей I (х, у) двухмерного изображения, к некоторому дискретному, т. е. символьному представлению. Замечательным свойством такого преобразования является то, что оно, судя по всему, не сопровождается потерями информации. Это утверждение еще не доказано и основывается на теореме Б. Ф. Логана. Теорема утверждает, что при выполнении определенных условий сигнал, ширина полосы частот которого составляет одну октаву, может быть полностью восстановлен (с точностью до мультипликативной постоянной) по точкам пересечения нулевого уровня, что иллюстрирует рис. 2.19.
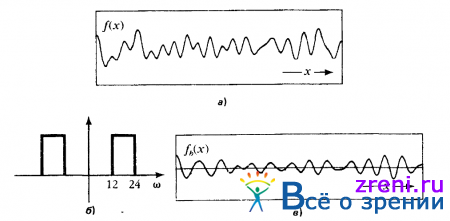
Рис 2.19. Сущность теоремы Логана. Если сигнал после фильтрации не имеет общих нулей с его преобразованием Гильберта, то согласно теореме Логана этот сигнал с точностью до некоторой мультипликативной постоянной определяется исключительно точками пересечения им нулевого уровня. Результат Логана имеет существенное значение для нижнего уровня обработки зрительной информации в том отношении, что (при соответствующих условиях) собственно точки пересечения сигналом нулевого уровня содержат очень важную информацию. а — вероятностный гауссовский сигнал f(x) с ограниченной полосой частот; б — полоса пропускания (в частотной области) идеального однооктавного полосового фильтра; в — результат фильтрации сигнала f(x)
Хотя доказательство теоремы трудное, оно, в сущности, показывает, что сигнал, ширина полосы частот которого меньше одной октавы, должен пересекать ось х по меньшей мере так же часто, как это должно происходить в соответствии с требованиями теоремы отсчетов.
Применительно к нашим задачам утверждение теоремы Логана, к сожалению, не обладает достаточной силой, чтобы на ее основании можно было выступать с какими бы то ни было непосредственными заявлениями о зрении. Эта проблема имеет двойственный характер. Во-первых, применительно к зрению пересечение нулевого уровня происходит в двух измерениях и часто нелегко распространить аргументацию теоремы отсчетов с одномерного случая на двухмерный. Во-вторых, оператор ?2 G не представляет, строго говоря, однооктавный полосовой фильтр: ширина его полосы пропускания, соответствующая половине энергии спектра, составляет 1,25 октавы, а чувствительности по уровню 0,5-1,8 октавы. С другой стороны, мы располагаем дополнительной информацией, а именно значениями углов, под которыми кривые, соответствующие сигналу, пересекают нулевой уровень - они примерно отвечают контрастности конкретного яркостного перехода на изображении. Очевидно, очень трудно аналитически решить эту задачу, однако Нисихаре удалось экспериментально получить обнадеживающие подтверждения той точки зрения, согласно которой изображение, обработанное с помощью некоторого двухмерного фильтра, поддается восстановлению по его точкам пересечения нулевого уровня и значениям углов этих пересечений
Рисунок 2.20
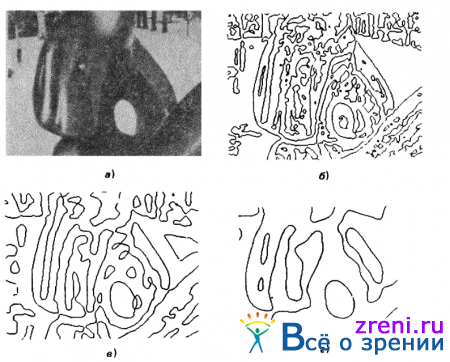
Рис. 2.20. Изображение, представленное на рис 2 20, а, свертывается с ?2 G-фильтрами, размеры рецептивных полей которых (W2-D = 2?2?) равны соответственно 6,12 и 24 пикселам Эти фильтры приблизительно перекрывают диапазон, в котором действуют фильтры, реализуемые в центральной ямке сетчатки глаза человека. Изображения, полученные в результате пересечений нулевого уровня, представлены на рис. 2.20, б, в и г соответственно. Обратите внимание на то, сколь тонкие детали выделяет фильтр с наименьшим рецептивным полем. В связи с получением такого набора изображений, по всей очевидности, возникнет следующая проблема каким образом всю эту информацию следует использовать для того, чтобы получить некоторое единое описание?
иллюстрирует тот этап, до которого мы дошли в нашем изложении На нем приведены исходное изображение одной из скульптур Хенри Мура и вид, который оно принимает на выходе трех каналов, осуществляющих фильтрацию на различных масштабных уровнях. Таким образом, на рисунке представлены пересечения нулевого уровня на исходном изображении после того, как оно было обработано с помощью ?2 G-фильтров, в случае когда гауссовские части G характеризуются разными пространственными постоянными Возникает следующий вопрос, что же следует делать со всей этой информацией?
↑ Необработанный первоначальный эскиз
До сих пор я тщательно избегал употребления термина яркостный переход, рассматривая обнаружение изменений яркости и их представления с помощью ориентированных отрезков пересечений нулевого уровня. Дело в том, что термин яркостный переход отчасти несет определенный физический смысл, например он наводит на мысль о реально существующей границе. До сих пор же речь шла исключительно о нулевых значениях сигнала, появляющихся на выходе некоторого набора полосовых фильтров, аппроксимирующих процедуру взятия второй производной. Мы не имеем права говорить о них как о яркостных переходах. Если же основания для этого имеются, следует указать, какие именно. Это различие имеет жизненно важное значение для теории зрения, а возможно, и для теорий других систем восприятия, поскольку краеугольным камнем зрительного восприятия является вывод, позволяющий по структуре изображения судить о структуре реального внешнего мира. Это как раз и служит предметом теории зрения, и основные ее проблемы связаны с физическими ограничениями и допущениями, обеспечивающими возможность получения указанного вывода.
Впервые с такими проблемами мы сталкиваемся в задаче, возникающей в связи с рис. 2.20. а именно: каким образом следует объединять информацию, поступающую по разным каналам? Реально используемые в зрительной системе рабочие полосы частот ?2 G-фильтров отстоят друг от друга на октаву или большую полосу частот, и потому у нас нет априорных оснований считать, что пересечения нулевого уровня, полученные с помощью фильтров с рецептивными полями разных размеров, связаны между собой. Существует, однако, физическая причина, благодаря которой они часто действительно связаны. Она является следствием первого из введенных нами в предыдущей главе физических допущений — условия пространственной локализованности. Реальный мир располагает следующими источниками, способными породить изменения яркости на изображении: 1) изменения освещения, в том числе теней, источников видимого света и углов освещения; 2) изменения расстояния от видимых поверхностей до наблюдателя или их ориентации относительно наблюдателя; 3) изменения коэффициентов отражения поверхности.
Решающим в данном случае является то обстоятельство, что все эти разновидности изменчивости можно считать (каждую по-своему) пространственно локализованными. Если не учитывать специфические дифракционные картины, то нельзя считать, что внешний мир, воспринимаемый зрительно, построен из зыбких, волнообразных пульсаций — непроизводных элементов, простирающихся над некоторой областью, образуя над ней некоторую суммарную картину. В целом наблюдаемый мир образован контурами, складками, царапинами, метками, тенями и оттенками, причем все они пространственно локализованы. Таким образом, отсюда следует, что если различимые пересечения нулевого уровня имеются на изображении, обработанном с помощью ?2 G-фильтра с рецептивным полем некоторого размера, то эти пересечения должны быть обнаружены в том же месте изображения после обработки исходного изображениями фильтрами с рецептивными полями любых размеров, больших, чем у первого. Если такое положение не сохраняется при фильтрации с рецептивным полем большего размера, то это может происходить по одной из следующих двух причин: либо два или несколько локальных изменения яркости ’’объединяются” (их значения усредняются) в канале, соответствующем большему рецептивному полю, либо изменения яркости вызываются двумя независимыми физическими явлениями, возникающими в одной и той же области изображения, но на разных масштабных уровнях. Примером первой ситуации служит узкая полоса, края которой точно локализуются каналами, с малыми рецептивными полями; при использовании же больших рецептивных полей этого не происходит. Подобные ситуации можно распознавать по наличию двух близко расположенных пересечений нулевого уровня при использовании каналов с малыми рецептивными полями. Примером второй ситуации служит наложение тени на участок с резким изменением отражательной способности некоторой поверхности, что распознается по смещению пересечений нулевого уровня, получаемых в каналах с большими рецептивными полями, относительно пересечений нулевого уровня, получаемых в каналах с малыми рецептивными полями. Если тень имеет точно такие же положение и ориентацию, что и соответствующий участок поверхности, то позиции точек пересечения нулевого уровня могут оказаться недостаточной информацией для разделения этих двух физических явлений, однако при решении реальных задач такой случай встречается редко.
Итак, реальный физический мир налагает ограничения на геометрическую организацию пересечений нулевого уровня, получаемых с помощью каналов с рецептивными полями разных размеров. Мы можем воспользоваться этим обстоятельством, сформулировав допущение о совпадении в пространстве:
eсли некоторый отрезок пересечений нулевого уровня воспроизводится на выходе ряда независимых каналов ?2 G-фильтрации, выполняемой с рецептивными полями близких размеров, причем данный отрезок во всех каналах имеет одни и те же позицию и ориентацию, то наличие набора таких отрезков пересечений нулевого уровня свидетельствует о том, что на изображении имеется изменение яркости, вызванное каким-то одним физическим явлением (изменением коэффициента отражения поверхности, освещения, глубины или ориентации поверхности).
Другими словами, если пересечения нулевого уровня, получаемые от независимых каналов с рецептивными полями смежных размеров, совпадают, то их можно относить к одному источнику. Если же пересечения нулевого уровня не совпадают, то они, по всей вероятности, порождаются различными поверхностями или различными физическими явлениями. Это означает, что: 1) минимальное число каналов ?2G-фильтрации, необходимое для учета реалий физического мира, равно двум; 2) если имеется некоторый диапазон размеров рецептивных полей каналов фильтрации, который достаточно рационально разнесен в частотной области и перекрывает необходимый диапазон частотного спектра, то можно сформулировать правила объединения соответствующих пересечений нулевою уровня в некоторое описание, непроизводные элементы которого имеют физический смысл.
Хотя такие правила весьма сложны, поскольку они должны учитывать множество частных случаев, общий принцип их построения вполне очевиден. При условии, что пересечения нулевого уровня, соответствующие каналам с большими рецептивными полями, ’’представляются” тем, что удается обнаруживать с помощью каналов с меньшими рецептивными полями (либо благодаря наличию взаимно однозначного соответствия этих пересечений с пересечениями нулевого уровня в каналах с меньшими рецептивными полями, либо благодаря тому, что первые являются размытыми усредненными копиями вторых), все эти данные характеризуют физические реальности, которые и составляют приблизительно наблюдаемое по каналам с меньшими рецептивными полями и, быть может, несколько сглаженное в результате снижающего шум и усредняющего воздействия каналов с большими рецептивными полями. Для того чтобы определить, имеет ли такое ’’представление” место в действительности, необходимо выявить те конфигурации, в которых-пересечения нулевого уровня, полученные с помощью каналов с малыми рецептивными полями, расположены близко друг от друга. Дело в том, что при этом каналы с большими рецептивными полями могут ’’обмануться”. Отсюда и вытекает необходимость обнаружения и выделения пространственных конфигурации типа узких полос и пятен.
Если же пересечения нулевого уровня, соответствующие каналам с большими рецептивными полями, не представляются теми пересечениями нулевого уровня, которые выявляются каналами с меньшими рецептивными полями, то необходимо ввести новые элементы описания, поскольку каналы с большими рецептивными полями регистрируют воздействия каких-то иных физических явлений. Такие ситуации могут возникать по ряду причин, скажем когда неясная тень или сфокусированная сетка накладываются на расфокусированное изображение ландшафта или когда мы видим, как водяной жук скачет по ряби на поверхности пруда, а водоросли, растущие на его дне, создают расфокусированный фон.
Описание изображения, к построению которого ведет такой подход, называют необработанным первоначальным эскизом. В нем используются такие непроизводные элементы, как яркостные переходы, полосы, пятна и концы, причем каждому из них ставятся в соответствие признаки, характеризующие его ориентацию, контрастность, длину, ширину и местоположение на изображении. Соответствующий пример приведен на рис. 2.21.
Рис 2.21. Необработанный первоначальный набросок, полученный с помощью двух каналов а, 6 — пересечения нулевого уровня для изображения, приведенного на рис. 2.12, е помощью фильтров, у которых w2-D равно 9 и 18 пикселам соответственно; поскольку канал с большим рецептивным полем не дает ни одного пересечения нулевого уровня, которое не соответствовало бы пересечению нулевого уровня, полученному с помощью канала с малым рецептивным полем, расположение яркостных переходов в едином описании также соответствует представленному на рис. 2.21,а; в, г и д — символьное представление признаков, приписанных к местоположениям яркостных переходов, представленным на рис. 2.21, а (в — пятна; г — локальные ориентации отрезков яркостных переходов, д — полосы). Эти диаграммы представляют лишь пространственную информацию, содержащуюся в признаках. Типичными являются следующие полные описания непроизводных элементов
Непроизводные элементы, которые характеризуются этими описаниями, отмечены стрелками Размещающая способность анализа изображения, приведенного на рис. 2.12, примерно соответствует тому, что увидел бы человек, рассматривая его с расстояния около двух метров
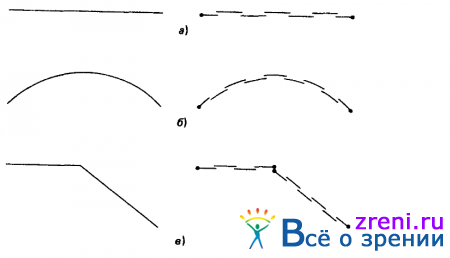
Его можно рассматривать как некоторое бинарное отображение (рис. 2.21, а), определяющее точное местоположение на изображении отрезков яркостных переходов и указывающее для каждой точки этих отрезков локальную ориентацию, а также характер и степень изменения яркости (рис. 2.21, г). Непроизводные элементы — пятно (рис. 2.21, в), полоса (рис. 2.21, д) и разрыв (непрерывности) , или конец, - можно выделять на изображении в явном виде точно таким же образом. Представление некоторой длиной прямой задается, например, с помощью конца, нескольких отрезков одинакового направления, за которыми следует другой конец, как это показано на рис. 2.22, а.
Рис. 2.22. Необработанный первоначальный эскиз, задающий представление прямой в виде конца, нескольких направленных отрезков и второго конца (а). При замене прямой на гладкую кривую направление соответствующих внутренних отрезков будет постепенно изменяться (б). Если направление прямой резко изменяется, то ее представление должно включать явное указание о том, что имеется разрыв непрерывности. Следовательно, при использовании такого представления сохранение гладкости и непрерывности предполагается до тех пор, пока обратное не утверждается в явном виде.
Ширина, контрастность и направление, вообще говоря, определены для всех точек прямой, хотя с практической точки зрения было бы вполне достаточно задавать эту информацию для соответствующим образом определенного интервала выборки. Если ширина прямой оказывается больше диаметра w наименьшего из используемых рецептивных полей, то для каждой из ее сторон строятся независимые описания яркостных переходов. Если линия изгибается, ориентация будет постепенно изменяться по ее длине (рис. 2.22, б). Если в некоторой точке линии имеется разрыв непрерывности по ориентации, то его положение определяется некоторым указанием на наличие конца или разрыва непрерывности (рис. 2.22, в).
Необработанный первоначальный эскиз представляет собой очень богатое описание изображения, поскольку содержит, в сущности, все информацию, имеющуюся в пересечениях нулевого уровня, полученных с помощью нескольких каналов (двух — в примере, приведенном на рис. 2.21). Важность этого представления заключается в том, что оно является представлением изображения, непроизводные элементы которого с высокой степенью вероятности непосредственно отражают физическую реальность.
Субъективно Вы воспринимаете существование необработанного первоначального эскиза, но не воспринимаете пересечения нулевого уровня, из которых этот первоначальный эскиз построен. Для того чтобы увидеть, что каналы с большими рецептивными полями сообщают Вашему мозгу, Вам приходится прищуриваться или каким-либо иным способом расфокусировать изображение. Только так, например, Вы сможете увидеть изображение Авраама Линкольна на его портрете, подвергнутом Л. Д. Хармоном дискретизации и квантованию (рис. 2.23),
Рис. 2.23. Пример, показывающий, что человек в состоянии воспринимать не собственно пересечения нулевого уровня, а лишь те описания, которые им порождаются в необработанном первоначальном эскизе: а — портрет Авраама Линкольна, подвергнутый Л. Д. Хармоном дискретизации и квантованию (никакие сознательные усилия не позволяют нам увидеть изображение Линкольна, если мы только не расфокусируем изображение или как-то не скосим глаза, несмотря на то, что каналы с большими рецептивными полями обеспечивают получение пересечений нулевого уровня, дающих приближенное представление изображения лица Линкольна) ; б, в, г — пересечения нулевого уровня, полученные с помощью оператора ?2 G с рецептивными полями трех размеров, использованных при обработке изображения на рис. 2.20.
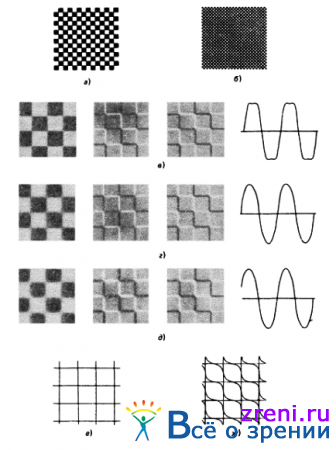
и прямые, пересекающие по диагонали шахматную доску (рис. 2.24).
Рис. 2.24. Вся энергия фурье-спектра изображения шахматной доски (бесконечного размера) приходится на диагонали, а по горизонтали и вертикали она равна нулю Тем не менее можно убедиться в том, что на рис 2.24, а вертикальная, горизонтальная и диагональная организации в равной степени поддаются наблюдения, в то время как на рис. 2.24, б диагональные конфигурации выглядят несколько отчетливее остальных. На рис. 2.24, в, г и д приведены результаты анализа, основанного на использовании пересечений нулевого уровня, которые получены с помощью операторов ?2 G с рецептивными полями, размер которых w2-D равен 12, 24 и 48 пикселам соответственно, исходное изображение состоит из квадратов со стороной, равной 24 пикселам, так что диапазон изменения размера рецептивного поля простирается от половинного до двойного значения длины стороны квадрата В первом столбце приведены результаты использования процедуры свертки Во втором столбце представлены пересечения нулевого уровня, причем значения углов, под которыми эти пересечения происходят, передаются как яркости (положительный и отрицательный контрасты - яркостями светлого и темного тонов) В третьем столбце все пересечения нулевого уровня имеют одинаковые яркости, и наконец, четвертый столбец содержит поперечные сечения результатов процедуры свертки в окрестности контуров пересечений нулевого уровня Рис. 2.12, д и е иллюстрирует описания, полученные с помощью каналов с рецептивными полями, соответственно много меньших и много больших размера квадрата изображения шахматной доски; эти описания следует сопоставить с тем изображением шахматных досок (рис 2 24, а и б), которые Вы воспринимаете Обратите, в частности, внимание на то, что пространственная организация изображения на рис. 2.24, б воспринимается как диагональная
Хотя каналы с большими рецептивными полями ’’видят” эти объекты, как показано на рис. 2.23, то, что они видят, адекватно представляется пересечениями нулевого уровня, получаемыми с помощью каналов с меньшими рецептивными полями. Ситуация, однако, изменяется при удалении частот средней части спектра в результате обработки портрета Линкольна. После этой операции процессы, обеспечивающие объединение пересечений нулевого уровня, которые соответствуют каналам разного размера, не обнаруживают связей между тем, что ’’видят” каналы с меньшими рецептивными полями, и тем, что ’’видят” каналы с большими рецептивными полями. В результате и те и другие порождают непроизводные элементы необработанного первоначального эскиза Именно поэтому, как установили Хармон и Джулес, Вы видите изображение Авраама Линкольна за ясно различимыми квадратами, на которые разделено изображение Первоначальный эскиз предполагает, что информация двух различных типов порождается двумя различными физическими явлениями, и в результате мы видим и то и другое.
↑ Методологическое отступление
Интересно, что зрительная система придает такое значение этому пространственному, основанному на использовании физических ограничений подходу. Она явно не допускает восприятия необработанных пересечений нулевого уровня как таковых. Очевидно, требуются еще и дополнительные данные типа совпадения с пересечениями нулевого уровня, соответствующими другому каналу. Считается, кроме того, что пересечения нулевого уровня служат исходной информацией для процесса установления соответствия между изображениями стереопары. В этом случае также объединяется исходная информация, поступающая по двум каналам, но относящимся к разным глазам. Аналогичные положения справедливы и для анализа, основанного на избирательности по направлению движения, которое, очевидно, определяется на уровне пересечений нулевого уровня. Однако и в этом случае, вероятно, возможность их использования зависит от наличия дополнительной информации — на этот раз, когерентности локальных перемещений в поле зрения. Вывод состоит в том, что собственно пересечения нулевого уровня не являются достаточной информацией. Этот вывод имеет решающее значение для данного подхода в целом, а именно: зрительная система старается иметь дело лишь с физически реальными объектами и для построения новых описаний, которые снова допускают физическую интерпретацию, используют правила, в основе которых лежат ограничения, определяемые физической структурой реального мира.
Это означает, что при формулировании теоретических положений необходимо проявлять исключительную тщательность, поскольку, судя по всему, природа была чрезвычайно внимательна и точна в процессе развития зрительной системы человека. В этом отношении очень полезно располагать в качестве основы тремя в явном виде определенными уровнями представления. Сформулировав информационную теорию некоторого процесса, Вы наводите существенный и конструктивный порядок в соответствующей области. После этого исчезает возможность говорить о некотором механизме, как будто бы имеющем нечто общее с исследуемой задачей, утверждая, что этот механизм действует как соответствующий процесс. Теперь требуется точно установить, что именно действует, и быть готовым привести необходимые доказательства. Установление соответствия между изображениями стереопары, например, похоже на множество других процедур, но не идентично ни одной из них. Эта процедура похожа на корреляцию, но не является ею. И если она трактуется как корреляция, то выбранные методы ненадежны. Задача синтеза стереоскопического изображения сводится к установлению соответствия между объектами, имеющими определенные физические прототипы, поскольку законы физики гарантируют возможность нахождения соответствия лишь между такими объектами, которые являются отображениями некоторых реальных физических объектов, занимающих вполне определенное положение в реальном пространстве материального мира. Для пикселов тонового изображения это условие не выполняется, следовательно, использование корреляции по уровням яркости не дает искомого результата.
Аналогичным образом поиск структуры изображения с привлечением представлений, относящихся к нескольким масштабным уровням, имеет сходство с методами фильтрации изображения с помощью различных полосовых фильтров. Кампбелл, например, для определения мелких деталей изображения танка, скажем, его регистрационного номера, предложил использовать фильтр верхних частот, а для получения его общих очертаний, свидетельствующих о том, что на изображении действительно имеется танк,— изображение, пропущенное через фильтр нижних частот. В данном случае дело снова обстоит таким образом, что, как и в случаях корреляции по уровням яркости и стереопсиса, эта концепция, основанная на территории фурье-преобразований, выглядит похожей на искомую, но не является ею. Структура реального физического мира не дает нам оснований для заключения, скажем, о том, что изображение, пропущенное через фильтр нижних частот, содержит важную информацию о физической и пространственной организации реального мира на этом масштабном уровне. Шахматная доска, изображенная на рис. 2.24, поможет нам разобраться в том, почему это так. Одна из важных особенностей организации этого изображения заключается в том, что черные и белые квадраты образуют не только строки и столбцы, но и диагонали. Несомненно, использование фильтров, полоса пропускания которых выбрана в низкочастотной области спектра, может дать нам информацию относительно диагональной организации изображения, но отнюдь не о горизонтальной и вертикальной, а механизмы, предназначенные для выделения горизонтальных и вертикальных конфигураций (с помощью введения обобщенных признаков-квадратов и установления характера их группировки), обеспечат также и выделение диагональных конфигураций. Таким образом, подход, основанный на использовании фильтрации, не является ни необходимым, ни достаточным.
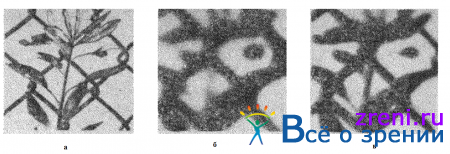
Другой пример связан с рисунком ”в елочку”, который приведен на рис. 2.2. Вертикальная структура, образованная этими полосами, наглядно демонстрирует разновидность пространственной организации, причем последнюю нельзя выделить методами, основанными на фурье-преобразованиях, поскольку энергия спектра в вертикальном направлении равна нулю. Такая пространственная организация, однако, легко выявляется с помощью методов, реализующих пространственный физический подход; отправной точкой в этом случае служит некоторое представление изменений яркости на исходном изображении, после чего используются процедуры группировки, в которых в качестве основных критериев применяются подобие, пространственная близость и тип конфигураций, которые, требуется получить. Мейхью и Фрисби одними из первых оценили важность этого обстоятельства в экспериментах, по изучению способности человека решать задачи, связанные с различением текстур, и получили дополнительные данные в подтверждение его справедливости. Позже мы еще вернемся к их работе.
И наконец, рассмотрим некоторые данные, свидетельствующие о выявлении на этом этапе концов, и их значение. Я считаю, что сейчас уместно заняться этими данными, поскольку, хотя яркостные переходы, полосы и пятна — это достаточно очевидные объекты, концы имеют существенно более представительный и абстрактный характер. Читателю, таким образом, могут потребоваться дальнейшие доказательства того, что эти объекты действительно порождаются на достаточно низком уровне.
На рис. 2.25
Рис. 2.25. Примеры выделения концов: а, б — субъективные контуры, построенные при объединении тех точек, в которых линии обрываются; в — точки нарушения непрерывности по направлению, образующие прямую; г — концы или нарушения непрерывности небольших Горизонтальных прямых на изображениях, образующих стереопару (сопоставляются, очевидно, в процессе поиска соответствий, что приводит к получению изображения квадрата, обладающего некоторой глубиной)
приведено несколько соответствующих примеров. Мы определили конец как некоторое нарушение непрерывности ориентации пересечений нулевого уровня или как точку, в которой заканчивается полоса. На рис. 2.25, a-в представлены примеры случаев, когда концы объединяются и когда трудно предложить метод, позволяющий это установить без определения явно истинных позиций нарушений непрерывности. Еще интереснее рис. 2.25, г, поскольку объекты, соответствие которых устанавливается в этой стереопаре, представляют собой, очевидно, малые разрывы непрерывности в горизонтальных прямых, причем стереоскопичность для этих изображений сохраняется даже в случае мельчайших нарушений непрерывности — менее 20". Таким образом, подобные концы используются не только для стереопсиса (точно так же, как мы субъективно воспринимаем их существование), но, судя по всему, является стандартной практикой даже в тех случаях, когда нарушения непрерывности относятся к диапазону повышенной остроты зрения (меньше размера рецептора сетчатки). Поразительным механизмом является зрительная система человека!
---
Статья из книги: Зрение | Марр. Д.


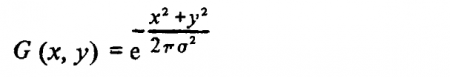
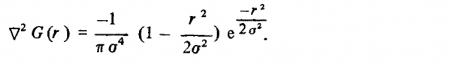
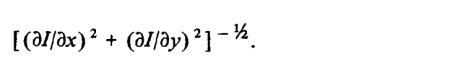





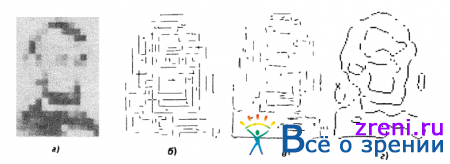

Комментариев 0