Инерция зрения

Содержание:
Описание
↑ Механическая аналогия
При заточке на точильном круге стального инструмента из него вырывается веер искр — яркие полосы длиной 30—60 см. Это раскаленные крупинки наждака и стали, быстро пролетающие в воздухе. Но видим мы не движущуюся крупинку, а всю ее траекторию одновременно: когда крупинка остывает и погасает в конце своего пути, глаз еще сохраняет впечатление от ее яркости в момент вылета. Здесь наглядно проявляется инерционность зрительной системы или, короче, инерция зрения.
Слово «инерция» прежде всего утвердилось в механике и стало там одним из основных понятий. Движение по инерции в механике может продолжаться сколь угодно долгое время: движение планет в солнечной системе длится миллиарды лет. На Земле же всегда имеются силы сопротивления, и поэтому движение по инерции в земных условиях длится недолго. Именно в таком смысле, как сравнительно недолгое последействие, термин «инерция» стал входить в другие области науки. Например, академик С. И. Вавилов применяет этот термин к явлениям люминесценции. Инерция люминофора выражается в продолжении его свечения после удаления возбуждающего света или другого энергетического воздействия. Инерцию Вавилов вводит даже в основное определение люминесценции. Будучи одним из видов излучения, люминесценция неизбежно связана с затратой энергии, и, следовательно, свечение «по инерции» всегда более или менее быстро затухает.
В таком же смысле говорят и об инерции зрения. Развитие зрительного впечатления можно сравнить с движением тела в вязкой среде. Аналогия, хотя и формальная, может помочь уяснению развития зрительного впечатления во времени.
Пусть шар, масса которого М, движется под действием силы f(t) в вязкой среде. По закону Стокса сила сопротивления движению шара пропорциональна его скорости v. Коэффициент пропорциональности обозначим через R: он в свою очередь пропорционален радиусу шара и вязкости среды. Движение шара описывается уравнением
Пусть в момент t = 0 скорость ? = 0. Сила в промежуток времени от 0 до t1 имеет постоянное значение f1 а после момента t1 она равна нулю. Тогда интегрирование уравнения для интервала 0 ? t ? t1 даст
а для t > t1
где ? = M/R, a ?1 — скорость в момент t1.
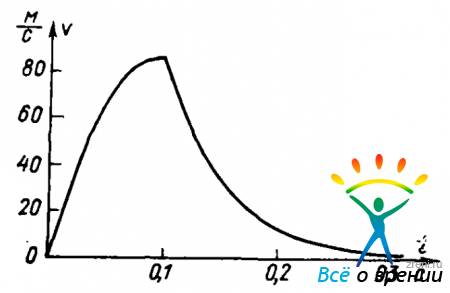
Мы видим, что скорость тела непропорциональна действующей силе. Пропорциональность наступает только после бесконечно долгого действия силы, когда оказывается, что t ? ?, но меньше t1 [см. формулу (62)]. Но величина ? прямо пропорциональна массе тела М, т. е. величине, характеризующей ею инерционность: чем больше инерция, тем дольше нестационарный процесс. На рис. 32
Рис. 32. График движения тела в вязкой среде
изображен график скорости тела массой в 1 кг, на которое в течение 0,1 с действует сила 20 Н, причем R = 20 кг/с.
Примерно такую же форму будет иметь график зависимости ощущения S от яркости L, которая воздействует на глаз в течение 0,1 с. П-образный импульс яркости вызывает постепенный подъем ощущения яркости, которое за 0,1 с не достигает значения, соответствующего долговременному действию той же яркости. После прекращения действия света S постепенно спадает, приближаясь к нулю.
↑ Эффективная яркость
Для перехода от общих рассуждений и аналогий к точным формулам необходимо условиться, что обозначаем мы символом S, вместо расплывчатого термина «ощущение» ввести какую-то определенную, измеримую хотя бы принципиально величину. Такую величину мы назовем эффективной яркостью. Ощущение есть факт нашего сознания, и ни психология, ни физиология не выработали методов его количественной оценки. Остается один способ: проектировать ощущение обратно во внешний мир и сравнивать его с ощущением от других аналогичных раздражений.
При обычном визуальном фотометрировании сравниваемые яркости действуют на глаз достаточно долгое время. За длительное время между яркостью и ощущением яркости устанавливается однозначная зависимость. Поэтому можно было бы положить, что ощущение длительно действующей яркости просто равно этой яркости. Однако наблюдения и опыт говорят, что ощущение пропорционально скорее логарифму яркости, чем самой яркости (закон Вебера — Фехнера). Чтобы не вступать в конфликт с установившимися представлениями, мы ввели другой термин — «эффективная яркость», считая, что эта величина однозначно связана с ощущением яркости. Обозначим ее Lэ. Характер их связи, в сущности, не имеет значения. Будем считать только, что эта связь прямая, т. е. с увеличением эффективной яркости растет и ощущение яркости. Значит, при длительном действии яркости эффективная яркость Lэ однозначно зависит от L, и мы можем считать, что в этом случае обе величины просто равны друг другу: Lэ = L.
Что же мы выиграли от введения новой величины? То, что эффективная яркость Lэ перестает быть равной яркости L, как только L становится величиной, переменной во времени. Здесь уже нарушается однозначная зависимость между действующей в данный момент яркостью и ощущением яркости, эффективная яркость Lэ перестает быть равной действующей яркости L и начинает по-настоящему выполнять свои функции количественной характеристики зрительного ощущения. Так, например, если яркость 100 кд/м2 подействует на глаз в течение 0,02 с, эффективная яркость не превысит 40 кд/м2.
Для пояснения изложенного приведем аналогию с фотоэлементом. Представим себе фотометр, состоящий из фотоэлемента и стрелочного гальванометра, шкала которого проградуирована в люксах. Конечно, показания гальванометра будут соответствовать освещенности фотоэлемента только при условии, что освещенность достаточно долгое время остается постоянной. Осветим фотоэлемент так, чтобы освещенность 100 лк действовала на него только 0,1 с. Стрелка покажет, например, 12 лк и вернется на 0. Значение 12 лк здесь нельзя, конечно, считать освещенностью, но можно назвать эффективной освещенностью. При переменной освещенности фотоэлемента гальванометр в каждый данный момент будет показывать какое-то число — эффективную освещенность. Соотношение между истинной и эффективной освещенностью будет зависеть от инерционных свойств системы, т. е. от инерции фотоэлемента, индуктивности проводов и гальванометра и момента инерции подвижной части гальванометра.
Конечно, измерить эффективную яркость много труднее, чем эффективную освещенность в этом примере с фотометром. Однако принципиально такое измерение возможно, а в некоторых случаях даже легко осуществимо. Так, например, если яркость поверхности 100 раз в секунду принимает значения то 0, то 100 кд/м2, причем темные и светлые промежутки времени равны между собой, эффективная яркость оказывается постоянной и ее можно измерить обычным визуальным фотометрированием. Равна она в данном случае 50 кд/м2. При соблюдении некоторых предосторожностей фотометрированием может быть найдена и эффективная яркость отдельной короткой вспышки. Отсюда вытекает и наиболее наглядная формулировка самого понятия «эффективная яркость». Эффективной яркостью некоторого поля в данный момент мы называем величину, равную яркости второго поля, с которым первое может быть фотометрически уравнено визуальным способом, причем яркость второго поля длительное время сохраняет постоянное значение.
↑ Вычисление эффективной яркости
Установим некоторое формальное математическое соотношение между яркостью L(t) и эффективной яркостью Lэ(t), рассматривая обе величины как функции времени t.
Зрительный процесс состоит из ряда дискретных элементарных актов, начиная с поглощения отдельных фотонов и кончая передачей импульсов возбуждения по зрительному нерву. Но в известных границах можно пользоваться и для яркости и для эффективной яркости их средними значениями и применять плавные, сглаженные кривые функциональных зависимостей.
Начнем с рассмотрения dLэ— бесконечно малого изменения эффективной яркости за бесконечно малый интервал временя dt. Конечно, dLэ должно зависеть от L(t)—яркости, действующей на глаз за время dt. Но dLэ зависит не только от L(t). Пусть сотую секунды тому назад всякая яркость перестала действовать на глаз и в настоящий момент L(t) = 0. Но вследствие инерции зрения dLэ? 0 и Lэ ? 0. Эффективная яркость еще не стала равна нулю, но она уменьшается, затухает и, следовательно, dLэ < 0. Для отыскания связи между dL и dLэ необходимо знать закон, по которому происходит затухание эффективной яркости. Однако на этапе чисто математического исследования достаточно ввести функцию затухания формально, не устанавливая пока ее конкретного вида.
Отличная от нуля яркость L(t) вызывает процесс, приводящий к увеличению эффективной яркости, но идущий одновременно со спонтанным ее уменьшением вследствие затухания. Обозначим через dL'э увеличение эффективной яркости, обусловленное воздействием яркости L(t). Естественно предположить, что в малом интервале времени dL'э пропорционально L(t) и dt:
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
где С — коэффициент пропорциональности.
Определим теперь эффективную яркость для некоторого момента t = ?. Для этого недостаточно проинтегрировать dLэ от —? до ?, так как в выражении (64) не учтено спонтанное убывание эффективной яркости со временем. От элемента эффективной яркости dLэ, возникшего за время t, к моменту ? останется только некоторая часть dLэ, причем отношение dLэ/dL'э будет тем меньше, чем дольше шло затухание, т. е. чем больше промежуток времени ? — t. Иначе говоря,
где А означает некоторую функцию промежутка времени ? — t— функцию затухания.
Итак,
Именно dLэ, а не dL'э следует интегрировать, чтобы получить эффективную яркость в момент ?:
Для выяснения смысла коэффициента С положим, что на глаз длительное время действует постоянная яркость L1. Тогда по определению Lэ(?) = L1, т. е.
откуда
Интеграл не зависит от избранного значения т. Действительно, введем новую переменную х = ? — t; для нее dx = —dt. Нижний предел станет теперь +?, а верхний обратится в 0. Вместо минуса перед интегралом поменяем местами верхний и нижний пределы и получим
Перепишем формулу (67), пользуясь формулой (68), и вернемся к прежней переменной t (так как символ переменной интегрирования не влияет на значение интеграла):
Из формулы (65) видно, что функция затухания А — величина безразмерная. Следовательно, интеграл в формуле (69) имеет размерность времени, откуда размерность С — с-1. Введем величину, обратную С:
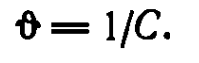
Тогда
↑ Время инерции
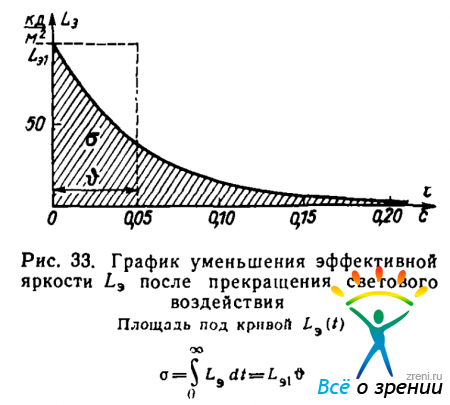
Для выяснения физического смысла величины ? представим себе, что некоторая постоянная яркость L1 действовала на глаз долгое время и прекратила свое действие в момент t = 0. Значит, при t = 0 эффективная яркость Lэ = L1 = Lэ1 (рис. 33).
Воспользуемся снова аналогией с движением тела в вязкой среде после прекращения действия силы — см. формулу (63).
Поставим вместо ?1 эффективную яркость в момент t = 0, т. e. Lэ1, а вместо
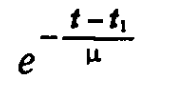
Кривая на рис. 33 изображает затухание эффективной яркости Lэ(t) после прекращения светового воздействия. Казалось бы, по кривой можно найти и время сохранения зрительного впечатления (назовем его ?), т. е. время, за которое Lэ(t) падает до нуля. Но Lэ(t) асимптотически приближается к оси времени, и указать точку Lэ(t) = 0 можно лишь условно. С таким затруднением сталкивались все исследователи времени сохранения. Сегнер нашел, что ? = 0,5 с; д’Арси получил ? =0,13 с, а Кавалло 0,1 с. Плато предлагает различать две величины-?1 — полное время сохранения зрительного ощущения и ?2 — время кажущегося постоянства зрительного ощущения. По Плато ?1 = 0,35 с; ?2 ? 0,01 с. Взглянув на рис. 33 и на формулу (70), мы видим, что ? равно отрезку оси времени, на котором строится прямоугольник, площадь которого Lэ1? равна площади под кривой затухания. Иначе говоря, ? — время, в течение которого сохранялось бы зрительное ощущение, если бы оно какое-то время сохранялось полностью (оставалось равным Lэ1), а потом сразу падало до нуля. Введенную нами величину ? — эффективное время сохранения зрительного впечатления будем называть далее временем инерции.
↑ Эффективные величины
Инерцию зрения приходится учитывать при расчете видимости:
- объектов, появляющихся на короткое время ?;
- быстро движущихся объектов;
- коротких вспышек точечных источников света.
↑ Эффективный контраст
Рассмотрим более подробно первый случай. Пусть наблюдатель непрерывно смотрит на экран, яркость которого L. На короткий промежуток времени т на экране появляется объект, яркость которого Ls Контраст объекта с фоном
Поскольку этот контраст существует только короткое время т, глаз воспримет эффективный контраст Кэ, который можно получить, подставив в формулу (72) вместо яркостей эффективные яркости:
Воспользовавшись формулами для эффективной яркости и произведя некоторые преобразования, получим
О функции затухания мы знаем только, что при t ? 0 А (t) стремится к единице, поэтому, если ? мало (? ? ?), то
и, следовательно,
Эффективный контраст во столько раз меньше обычного контраста, во сколько время экспозиции ? меньше времени инерции ?.
↑ Экспериментальное определение времени инерции
Формулы (74) и (75) дают возможность экспериментально определить как ?, так и функцию затухания. Принципиально для этого достаточно измерить пороговый контраст ? для какого-нибудь объекта при стационарном наблюдении, а потом при разных контрастах Кп доводить Кэ до порога видимости подбором времени экспозиции т. Получив целый ряд пар Кп и ? (индекс «п» показывает, что малое время экспозиции делает контраст пороговым), обращаем внимание на их произведения. Пока Кп? = const, мы можем пользоваться формулой (76) и подставив в нее Кэ = ?, найти ?. Затем ? и ? можно ввести в формулу (74) и, подставляя в нее те значения Кп, при которых Кпт ? const, и решая уравнения, получить ряд значений интеграла при разных т. По значениям определенных интегралов можно судить о виде подынтегральной функции.
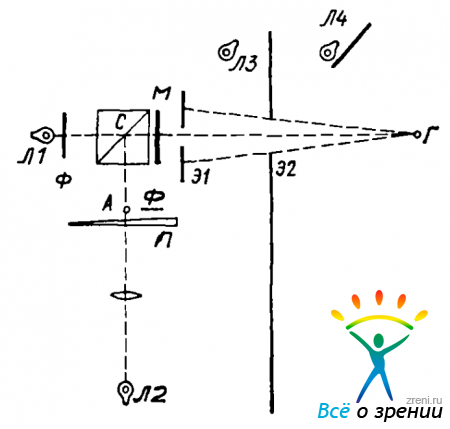
Схема экспериментальной установки изображена на рис. 34.
Рис. 34. Схема установки для измерения порогового контраста
Молочное стекло М освещено лампой Л1. Посеребренный кружок С на диагональной плоскости кубика отбрасывает тень на стекло М. Проекцию кружка С на молочное стекло будем называть маркой. Марка освещается лампой Л2, действительное изображение нити которой образуется в точке А. Система отъюстирована так, что при равенстве освещенностей на молочном стекле от ламп Л1 и Л2 марка совершенно не видна (К = 0). Освещенность от лампы Л2 можно регулировать посредством нейтрального клина П (поглотитель), обеспечивая полную невидимость марки.
Глаз наблюдателя помещался в точку Г (другой глаз прикрывался заслонкой). Яркость стекла М была 32 кд/м2, яркость экранов Э1 и Э2 с помощью ламп Л3 и Л4 поддерживалась на том же уровне. Наблюдатель помещался на трех различных дистанциях, которым соответствовали размеры марки 11', 7,3' и 5,5' (форма марки была овальной; за ее размер принимался диаметр равновеликого с овалом кружка).
Поместив наблюдателя на одной из дистанций, сначала определяли пороговый контраст ? многократным измерением смещения клина 17 в одну и другую сторону до того положения, при котором марка становится едва заметной.
По половине разности отсчетов в ту или в другую сторону находили ?, а клин ставили в среднее положение и приступали ко второму этапу эксперимента.
Нейтральный фильтр Ф, который при его установке в точку А создавал контраст К, прикрепляли к концу маятника. Экспериментатор отклонял маятник на 45° и отпускал его качаться. Сначала фильтр П проходил точку А за время т, столь короткое, что испытуемый не видел марки. Но амплитуда маятника сокращалась, и в какой-то момент испытуемый улавливал появление марки — мелькание. Экспериментатор отмечал угол а„ отклонения маятника, соответствующий первому появлению марки для испытуемого. Зная период маятника (1,79 с), длину фильтра П и угол ?п, легко сосчитать т. Каждому испытуемому предъявлялось 6 фильтров, создающих контрасты К, равные 100; 85; 79; 58; 28 и 20%. Было найдено, что пока т < 0,01 с, произведение Кп? практически постоянно. Подставляя Кп? и ? в формулу (76), получаем
Для трех наблюдателей при всех вышеуказанных размерах марки среднее время инерции оказалось равным пяти сотым секунды.
↑ Функция затухания
Определение функции затухания по немногим значениям ее интеграла — более сложная задача. Более ста лет тому назад Аллар высказал предположение, что зрительное впечатление убывает точно так же, как по закону Ньютона охлаждается тело малых размеров. Применительно к эффективной яркости Lэ этот закон можно записать в виде:
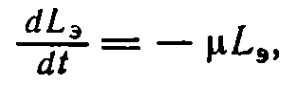
откуда
где Lэ1 — эффективная яркость в момент t = 0, когда перестала действовать на глаз яркость L1. Поскольку ц должно иметь размерность с-1, сопоставление (78) с формулами (66), (70), (71) и (74) дает
Результаты всех проведенных нами опытов с пороговым контрастом достаточно хорошо выражаются с помощью формул (79) — (82), которые мы называем формулами экспоненциальном зависимости. Замечательно, что формула (82) вполне соответствует формуле (62), т. е. между развитием зрительного ощущения и движением тела в вязкой среде действительно существует формальная аналогия.
↑ Эффективный контраст движущегося тела
На практике эффективный контраст Кэ, оказывается меньше контраста К чаще всего из-за быстрого движения контрастирующего объекта.
Когда наблюдается достаточно большой предмет и угловая скорость его не очень велика, глаза движутся вслед за объектом, его изображение на сетчатке сохраняется почти неподвижным и наблюдатель воспринимает его полный контраст с фоном К. Но для того чтобы взгляд начал следовать за предметом, его нужно заметить, хотя бы неясно, при неподвижном взгляде. Поэтому вопрос о пороговой видимости движущегося тела нужно решать для неподвижного взгляда.
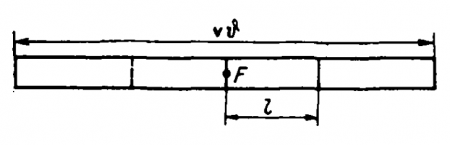
Пусть наблюдатель ожидает появления движущегося тела на поле, яркость которого L. Яркость тела Ls, длина его I, скорость v. Наблюдатель фиксирует точку F (рис. 35).
Рис. 35. Кажущееся удлинение движущегося тела
Момент, когда передний край тела касается точки F, примем за начало отсчета времени (t = 0). Конец тела коснется точки F в момент ?. В точке F наблюдатель длительное время до момента t = 0 видел фон, т. е. воспринимал действие яркости L. Только последнее время т он воспринимал в точке F яркость Ls. Время т легко вычислить. Очевидно, что
Подставив (83) в (74), получим
или, если l/? ? ?
Опишем простейший эксперимент, поставленный для изучения пороговой видимости движущегося тела. Установка состоит из двух белых дисков диаметром 1300 и 250 мм. На большой диск вдоль одного из радиусов наклеено 14 черных марок шириной d = 10 мм. и длиной l-1 мм (длиной марки мы называем ее размер в направленна движения; т. е. в данном случае перпендикулярно радиусу). Каждая марка находится- на своем расстоянии R от центра диска. Большой диск вращается с частотой v (56 либо 75 об/мин).
На малый диск наклеено 5 черных марок, каждая на расстоянии r от центра, шириной тоже 10 мм, а длиной lн= 3 мм. Диск вращается с частотой 100 об/с, так что каждая марка видна в виде серого кольца, эффективный контраст которого Кэ легко подсчитать, приняв во внимание, что контраст К неподвижной марки уменьшается во столько раз, во сколько l меньше длины окружности 2?r. Итак,
Эффективный контраст движущейся марки на большом диске можно подсчитать по формуле (85), выразив скорость ? через R и v:
Над обоими дисками помещены экраны с вырезанным сектором, через который и ведется наблюдение. Наблюдателю предлагается указать, какую из марок он еще замечает на большом диске и какую на малом. Получив таким образом два радиуса R и r, мы можем считать, что оба они соответствуют пороговому контрасту ? и, следовательно, при этих радиусах можно приравнять друг другу правые части формул (86) и (87). Решение получившегося уравнения дает
Следует заметить, что при движении тела изменяется не только его видимый контраст, но и видимая длина. Контраст К как бы размазывается на видимую длину l', которая отличается от истинной длины l на величину ??:
Так как пороговый контраст зависит от размеров объекта, видимое удлинение движущегося тела усложняет расчеты. Чтобы уменьшить возможную ошибку, мы, во-первых, ограничивали наблюдаемую картину вырезом в экранах, а во-вторых, делали марки достаточно большими: их ширина наблюдалась под углом 1,5°. Чем больше контрастирующий объект, тем меньше его пороговый контраст зависит от размеров.
Видимость движущегося тела изучалась и другими методами. В экспериментах участвовало 11 наблюдателей, что позволяло считать результаты достаточно надежными. Значение ? оказалось близким к ранее полученному ? = 0,05 с, причем обнаружилась некоторая зависимость от яркости, которая изменялась в пределах от 40 до 1000 кд/м2.
Во всех экспериментах с пороговым контрастом функция затухания хорошо аппроксимируется экспонентой [формула (81)].
↑ Эффективный блеск
Видимость точечных источников, вспыхивающих на короткое время, давно изучалась в связи с широким применением проблесковых огней для маяков. Наиболее определенный результат дали работы Блонделя и Рея. Чисто экспериментальным путем они нашли зависимость между блеском Е и длительностью проблеска точечного источника, наблюдаемого на темном фоне на пороге видимости:
Слева стоит величина, которую можно назвать экспозицией блеска. Она линейно зависит от длительности проблеска. Смысл коэффициента Е?, легко выясняется, если мы допустим, что проблеск становится очень длительным, т. е. ? ? ?. Тогда ? и ?+? можно сократить и мы получим Е = Е?. Значит, Е? — пороговый блеск при длительном действии источника. А ? — время инерции (приводя формулу Блонделя и Рея, мы позволили себе изменить обозначения величин).
Подобно тому как мы ввели понятие эффективного контраста, введем понятие эффективного блеска Еэ. По аналогии с формулой (74) напишем
Пороговый блеск Е? можно считать частным случаем эффективного блеска Еэ, поэтому есть основания предполагать, что для любого эффективного блеска будет тоже верна формула Блонделя и Рея, написанная так:
Приравняв друг другу значения Еэ, найденные по формулам
(91) и (92), получим
Теперь легко найти подынтегральную функцию — функцию затухания
Итак, из формулы Блонделя и Рея вытекает, что функция затухания — не экспонента, а гипербола второго порядка. Однако, прежде чем делать дальнейшие выводы, следует еще про верить допустимость применения закономерности (90), полученной Блонделем и Реем, к случаю эффективного блеска — формула (92).
↑ Видимость проблесковых огней
Нами были изучены при фовеальном зрении, на темном фоне (Т) и при разных яркостях фона (Ф) величины: пороговый блеск вспышек (соответственно ПТ и ПФ) и эффективный блеск проблесков (ЭТ и ЭФ). Кроме того, пороговый блеск проблесков был измерен при периферическом зрении. Во всех опытах применялась красная фиксационная точка, отстоявшая от точек, в которых происходили вспышки при фовеальном наблюдении, на расстояние 16', а при периферическом наблюдении — на расстояние 7°.
Установка позволяла давать либо одновременно две вспышки разной длительности и блеска, либо одну вспышку. При разной длительности вспышек они заканчивались одновременно. Результаты всех измерений укладываются в рамки линейной зависимости, т. е. подтверждают формулы (90), (92) и (94).
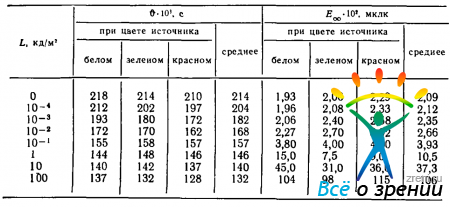
Пороговый блеск в темноте измерялся при двух вероятностях заметить вспышку, 50 и 80%- Значения О получены соответственно 0,205 и 0,200 с, т. е. очень близкими к найденному Блонделем и Реем ? = 0,21 с. Результаты пороговых наблюдений на фоне яркостью от 10-6 до 32 кд/м2 (ПФ) сведены в табл. 5.
Таблица 5. Зависимость порогового блеска Е?, и времени инерции ? от яркости фона L
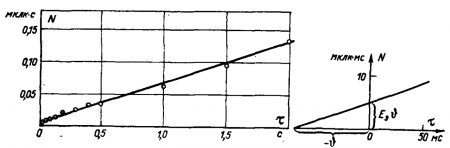
Для определения эффективного блеска Еэ на темном фоне (ЭТ) наблюдателю предъявлялись одновременно две вспышки: эталонная, блеск которой был Еi, а длительность ?0 = 0,01 с, и измеряемая, длительность которой т изменялась в каждой серии опытов от 0,01 до 2,5 с, а блеск ? подбирался таким, чтобы обе вспышки наблюдатель воспринимал одинаково яркими. Конечно, измерение Е с каждым наблюдателем повторяли многократно, чтобы найти среднее значение блеска. Затем находили значение Е, среднее для всех наблюдателей. Отложив произведение E? против значений т, проводили через экспериментальные точки прямую (рис. 36).
Рис. 36. График зависимости N = Е? от длительности проблеска ?
Полученная прямая выражается уравнением (92), что позволяет легко найти ее параметры Eэ и ?. Чтобы найти их графическим путем, перечертим часть графика, близкую к абсциссе ? = 0, в увеличенном масштабе (рис. 36, справа). Положив в формуле (92) E? = 0, получаем Ф = - ?; положив ? — 0, получаем E? = EЭ?. На рис. 36, справа указаны соответствующие отрезки координатных осей.
Для четырех значений эффективного блеска 0,064; 0,625; 11,3 и 28,6 мклк были найдены значения времени инерции: 0,078; 0,080; 0,044 и 0,035 с. Связь между Еэ и ? приближенно выражается формулой
Если даны блеск огня Е и его длительность т, эффективный блеск Еэ на темном фоне можно найти совместным решением уравнений (92) и (95).
Исследование эффективного блеска на фонах различной яркости L (ЭФ) было проведено для значений Еэ, представляющих наибольший практический интерес. По международному соглашению принято считать, что ночью постоянный огонь виден до тех пор, пока блеск его не станет меньше 0,2 мклк. Назовем величину Еmin = 0,2 мклк наименьшим блеском. Эта величина значительно превышает пороговый блеск E?, определенный в лабораторных условиях даже для не очень темного фона. К какой же яркости фона можно отнести официально принятую величину Emin? Видимо, к такой, при которой яркость фона еще не очень повышает пороговый блеск E?. Судя по данным табл. 5, такой яркостью можно считать L = 0,003 кд/мг, для которой E? = 0,025 мклк, и именно к ней отнести Emin = 0,2 мклк. Обозначив через ?Е отношение минимального блеска Emin к пороговому E?, найдем, что для L = 0,003 кд/м2 ?E = 8.
Число ?E можно назвать коэффициентом надежности. В своих экспериментах мы старались при каждой яркости фона иметь дело с таким эффективным блеском, который приблизительно в 8 раз превосходит пороговый, т. е. сохранять условие Eэ ? 8Е?.
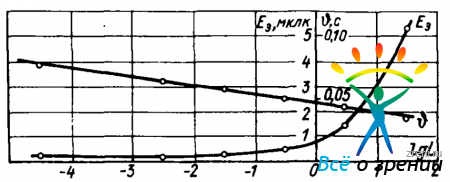
Так как экспозиция блеска Е? при каждой яркости и здесь линейно зависит от длительности проблеска ?, то, построив график, легко найти Еэ и ? (рис. 37).
Рис. 37. Время инерции ? и эффективный блеск Еэ в зависимости от яркости фона L
Эти данные не позволяют для любого сочетания Е, ? и L найти Еэ, но дают возможность оценить эту величину. Оценка заключается в том, что для данной яркости L по графику находят ?, а затем по формуле (92)—эффективный блеск Еэ. Нельзя утверждать, что полученное значение Еэ будет точным, но можно определить, больше оно или меньше, чем 8Е?, т. е. соответствует ли оно установленному коэффициенту надежности ?Е.
↑ Суммирование световых воздействий
Формулы линейной зависимости (90) и (92) указывают на способность зрения суммировать во времени воздействие входящего в глаз света и вместе с тем на ограниченность этой способности. За короткое время т суммирование происходит практически полностью; чем длиннее проблеск, тем хуже суммируется свет, т. е. тем больше должна быть общая световая энергия Е? для получения порогового восприятия или заданного эффективного блеска. Критерием для выяснения вопроса, мала или велика длительность т, служит сравнение ее со временем инерции ?. Рассмотрим два предельных случая.
Если ? ? ? формулы (90) и (92) дают
Справа стоят постоянные величины, т. е. суммирование происходит полностью, уменьшение ? в несколько раз может быть скомпенсировано увеличением во столько же раз длительности т. Формулы (96) соответствуют химическому закону Бунзена — Роско, согласно которому количество вещества, выделившегося в результате фотохимической реакции, пропорционально произведению интенсивности света и длительности воздействия. Применительно к зрению аналогичную закономерность называют законом Блоха.
Если ? ? ?, те же формулы дают
т. е. результат воздействия блеска на глаз перестает зависеть от длительности воздействия. Иначе говоря, если ? ? ?, глаз реагирует на световую энергию, а если ? ? ? — на световой поток (т. е. на мощность светового излучения).
Проведенные нами опыты с очень короткими (микросекунды) вспышками импульсных ламп подтвердили закон Блоха, т. е. формулы (96).
Формула Блонделя и Рея (90) и аналогичная ей формула (92) хороши именно тем, что они действительны во всем диапазоне возможного изменения длительности и в предельных случаях переходят в простые, неоднократно проверенные опытом зависимости (96) и (97). Кроме того, формула Блонделя и Рея связана с закономерностями, обнаруженными в электрофизиологии. В начале нашего столетия Вейс установил, что для порогового воздействия на мышцу сила тока i и длительность его действия т должны быть связаны соотношением
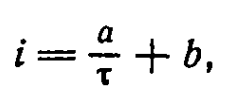
где а и b — постоянные.
Переписав формулу Вейса в виде
мы замечаем, что она вполне аналогична формуле Блонделя и Рея: произведение силы тока и его длительности при пороговом раздражении есть линейная функция длительности. Легко показать, что здесь b = i?, т. е. току, вызывающему пороговое сокращение мышцы при длительном воздействии, а a/b = ?, т. е. времени инерции, которое физиологи называют хронаксией.
↑ Два вида функции затухания
Из формулы Блонделя и Рея (функция затухания) однозначно выводится формула (94) как уравнение гиперболы второго порядка. Такова функция затухания для всех явлений, связанных с наблюдением блеска.
Но для всех явлений, связанных с наблюдением протяженных объектов, т. е. контрастов, функция затухания аппроксимируется экспонентой (79). Нужно сказать, что, в сущности, обе кривые не очень сильно отличаются друг от друга, но статистическая обработка большого количества экспериментов все же позволяет выявить различие.
Время инерции ? зависит от многих факторов, но в основном от яркости фона. Приближенно эту зависимость можно выразить формулой, дающем ? в секундах:
↑ Инерция и локальная адаптация
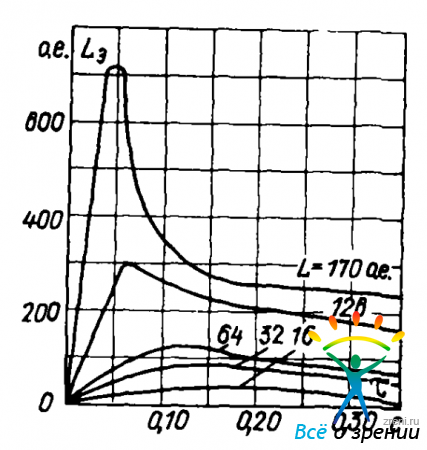
Введя в определение эффективной яркости сравнение полей переменной и постоянной яркости, мы в своих опытах никогда такого сравнения не производили. Непосредственному сравнению препятствует локальная адаптация сетчатки, что отчетливо проявилось в опытах Брока и Зульцера. Эти авторы фотометрически сравнивали два равномерно рассеивающих поля 1 и 2. Поле 1 освещают лишь короткое время т, так чтобы на нем создавалась освещенность E1 На поле 2 подбирали такую освещенность Е2. чтобы в момент освещения поля 1 яркость обоих полей показалась наблюдателю одинаковой. Результаты таких измерений изображены на рис. 38.
Рис. 38. График опыта Брока и Зульцера
Поскольку коэффициент отражения р у полей 1 и 2 был одинаков, яркости полей 1 и 2 были пропорциональны их освещенностям. Мы видим, что при ? ? 0,05 с эффективная яркость создаваемая яркостью 170 относительных единиц (о. е.), была более 700 о. е., а эффективная яркость Lэ, создаваемая яркостью 126 о. е.,— около 300 о. е. и т. д. Мы объясняем это тем, что к моменту появления яркости L1 яркость L2 уже давно воздействовала на то место сетчатки, где отображено поле 2, и чувствительность здесь понизилась. Остальная площадь сетчатки сохраняла более высокую чувствительность, и кратковременное воздействие яркости поля 1 дало сильно повышенный эффект. Качественно в правильности такого объяснения можно убедиться с помощью самого простого опыта. Положите на сильно освещенную белую бумагу кусок черной бумаги площадью примерно 16 см2. Смотрите в течение 30—40 с на середину черной бумаги, а затем, стараясь не поворачивать глаз, уберите ее. Вы ясно увидите на белом фоне еще более яркое пятно, которое быстро исчезнет.
Именно необходимость исключить влияние локальной адаптации заставляла нас для определения функции затухания и времени инерции избирать окольные пути. При пороговых измерениях световые воздействия на сетчатку слабы или мала разница между такими воздействиями и адаптационные изменения практически исключаются. Так исследовали мы пороговый контраст и пороговый блеск. При сверхпороговых измерениях эффективного блеска мы сравнивали изучаемый источник с эталонным, который тоже вспыхивал на короткое время. Таковы те предосторожности, которые следует соблюдать при определении эффективных величин.
----
Статья из книги: Глаз и свет | Луизов А.В.


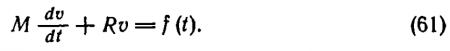




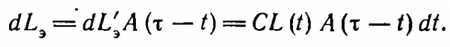
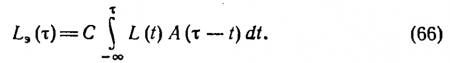
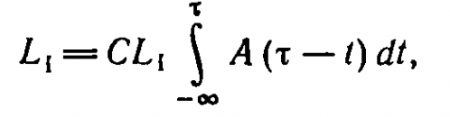
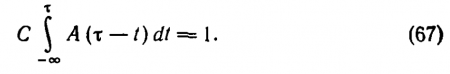
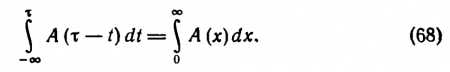













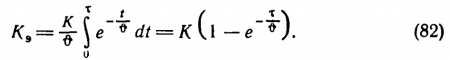










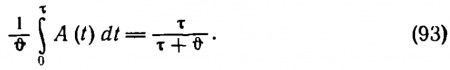

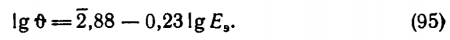
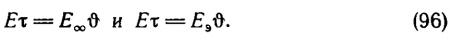


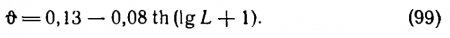
Комментариев 0