Стереопсис ? Часть 3.

Содержание:
Описание
Восприятие глубины при больших значениях диспаратности. Мы предполагаем, что зона Панума соответствует процессу слияния изображений стереопары в чистом виде. За пределами диапазона значений диспаратности некоторая возможность восприятия глубины все еще сохраняется, хотя это восприятие не соответствует точно истинному значению диспаратности. В этой связи целесообразно рассмотреть два следующих интересных случая.Первым из них является диплопия, при которой человек видит двойное изображение, но в то же время все еще воспринимает глубину. Алгоритмы установления соответствий между изображениями стереопары, описанные нами выше, предназначены для работы со сложными изображениями. Если изображения отличаются очень малой плотностью заполнения, при установлении соответствий между ними не возникает каких-либо проблем, так как в этом случае нет ложных целей, от которых приходится избавляться. Если, например, в заданном диапазоне значений диспаратности w вообще не находится допустимых соответствий, можно обратиться за соответствующей информацией к детекторам, действующим вне этого диапазона и, возможно, обеспечивающим обнаружение соответствий в более широком диапазоне. Идея здесь состоит в том, что при наличии определенных сведений о знаке диспаратности их может оказаться достаточно для ’’включения” вергентных движений глаз в необходимом направлении, с тем чтобы изображения были введены в пределы того диапазона значений диспаратности, в котором возможно достижение слияния.
Существует и другой способ использования таких детекторов. Как мы убедились, в разделе, посвященном информационной теории стереопсиса, если плотность заполнения изображения объектами, пригодными для установления соответствия, составляет ?, то плотность соответствий при правильном значении диспаратности равна ?, а при неправильных значениях диспаратности - всего лишь ?2. Если имеется некоторый набор детекторов диспаратности и нас интересует исключительно знак диспаратности, при которой соответствия устанавливаются правильно, можно воспользоваться вычислительной схемой, предусматривающей суммирование общего числа конвергентных соответствий (ложных целей и т. д.) и сопоставление результатов суммирования с соответствующим числом дивергентных соответствий. Можно рассмотреть различные способы реализации такой процедуры. Так, скажем, в самом простом варианте суммирование могло бы осуществляться одновременно по всему диапазону конвергентных и по всему диапазону дивергентных диспаратностей, однако вполне возможно и постепенное расширение области суммирования, до тех пор пока не будет получена существенная разность. Во всяком случае, при любой биологически достоверной реализации типа той, что проиллюстрирована рис. 3.21,
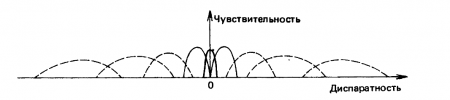
Рис. 3.21. Кроме трех групп детекторов, действующих в малых диапазонах значений диспаратности (их характеристики представлены сплошными линиями), могут существовать группы детекторов диспаратности, действующие за пределами основного диапазона (их характеристики представлены штриховыми линиями). Задача последних состоит в установлении того, дивергентно или конвергентно расположена плоскость слиятия, чтобы в соответствующем направлении начались вергентные движения глаз
следует ожидать уменьшения числа детекторов при увеличении значений диспаратности. Статистический анализ указывает, что в этом случае будет обеспечена психофизическая зависимость между диспаратностью стереограммы при отсутствии слияния и областью, необходимой для определения знака диспаратности.
Интересно, что Тайлер и Джулес установили наличие подобной связи для случая динамических сгереограмм, образованных случайными конфигурациями точек. В стереограммах такого типа конфигурации (но необязательно их диспаратности) изменяются со скоростью порядка 30 кадров в секунду. Знак диспаратности поддается определению (но не очертания диспаратного образа, например) при значениях диспаратности, доходящих до нескольких угловых градусов. Полученный ими результат - пропорциональность возможности определения знака диспаратности значению квадратного корня из размера области (?А) — можно объяснить с помощью схемы типа той, которая была предложена нами: в ней плотность детекторов диспаратности уменьшалась обратно пропорционально росту значений диспаратности, т. е. имела место зависимость 1 /d. В результате возникает ?А - зависимость. Конечно, этим результатам можно придать и иное толкование исходя из таких факторов, как движение либо возможное нелинейное покадровое суммирование во времени, осуществляемое на рецепторном уровне.
И наконец, вернемся к проблеме, которая все еще кажется мне загадкой стереопсиса, а именно: почему в качестве исходного представления для процесса установления соответствий между изображениями стереопары следует использовать пересечения нулевого уровня? Почему не подождать и не воспользоваться необработанным и полным первоначальными эскизами, применив схему с теми же общими характеристиками, но предусматривающую замену пересечений нулевого уровня, относящихся к низким пространственным частотам, приближенными крупномасштабными непроизводными элементами первоначального эскиза и пересечений нулевого уровня, относящихся к высоким частотам, необработанным первоначальным эскизом. Наблюдения Джулеса и Миллера, например, связанные с независимостью слияния по различным пространственным частотам, служат как будто бы наилучшим свидетельством в пользу варианта с одними пересечениями нулевого уровня, но, возможно, они поддаются объяснению и с помощью нашей альтернативной схемы Дело в том, что, поскольку в стереограммах, использованных Джулесом и Миллером, информация, которая относится к различным частям спектра пространственных частот, поступает не из одного источника, допущение о совпадении в пространстве нарушается и, следовательно, в первоначальном эскизе каждой пространственной частоте будут соответствовать независимые описания при возникновении стереоскопического слияния двух изображений.
Кроме того, мы располагаем данными Кидда, Фрисби и Мейхью, которые указывают на то, что некоторые виды границ на текстурах могут вызывать при стереопсисе вергентные движения глаз. Это служит явным свидетельством использования в стереозрении некоторых описаний, входящих в первоначальные эскизы на более поздних этапах обработки зрительной информации.
С другой стороны, однако, эта же группа исследователей обнаружила, что стереоскопическое слияние может, в некотором смысле, преобладать в зрительном распознавании текстур и тем самым, возможно, служит его предпосылкой (Фрисби и Мейхью. Несколько соответствующих примеров приведено на рис 3.22.
Рис. 3.22. Текстурные различия, ясно различимые монокулярно, исчезают при возникновении стереоскопического слияния двух изображений
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
При монокулярном рассматривании этих изображений на них ясно различаются области, текстурированные по разному, однако при бинокулярном рассматривании они сливаются. Этот факт является определенным, но отнюдь не бесспорным свидетельством в пользу подхода, предусматривающего использование пересечений нулевого уровня
Моя точка зрения состоит в том, что на самом деле применяется некоторая комбинация обоих методов, хотя в основе лежит метод, связанный с пересечениями нулевого уровня. Важнейшими преимуществами использования последних, очевидно, являются быстродействие (поскольку они определяются в первую очередь) и точность (поскольку их местоположение может определяться очень точно). Теоретические оговорки относительно пересечений нулевого уровня, сводящиеся к тому, что они лишь приближенно и ненадежно связаны с изменениями в реальном мире, не очень серьезны, поскольку пересечения нулевого уровня вполне физические (даже более, например, чем уровни серого тона). И это действительно так, поскольку реализация на ЭВМ теоретических положений, относящихся к пересечениям нулевого уровня, дала прекрасные результаты при работе с естественными изображениями.
Решили ли мы именно ту задачу, которую следовало решить? Основной проблемой, с которой сталкивается разработчик алгоритмов установления соответствий между изображениями стереопары, является определение того, какие задачи трудные и какие -нет. Нейрофизиолог мог бы с определенным основанием возразить, что проблема слияния изображений стереопары, в сущности, вовсе не так уж сложна, а действительно замечательным свойством стереозрения человека является его точность, которая может достигать столь высоких значений, как 2" при 75 %-ной норме успешного результата; это значение точности соответствует приблизительно 1/12 диаметра колбочки центральной ямки сетчатки. Он же мог бы отметить, что проблема ложных целей не является трудной, если соответствие устанавливается по признакам специального вида, которые встречаются на изображении весьма редко.
Я с этими аргументами не согласен в силу следующих причин. При установлении соответствий между изображениями стереопары решающее значение, несомненно, приобретает вопрос о том, насколько редко это редкое и каким образом редкость признака связана с рассматриваемым диапазоном значений диспаратности. Психофизические данные свидетельствуют о том, что те признаки, которые могут использоваться для установления соответствий, относятся к нижнему уровню и не отличаются какими-либо специфическими особенностями, связанными с контрастом или ориентацией. Так, стереограммы, образованные случайными конфигурациями точек, должны содержать ложные цели, тем не менее нам удается добиваться их слияния. Теоретический анализ, положенный в основу нашего второго алгоритма, в сущности, посвящен главным образом именно вопросу о том, насколько редко редкое, который самым тесным образом связан с допущением, что исходным представлением для процесса стереоскопического слияния изображений стереопары служат приближенно-ориентированные пересечения нулевого уровня, характеризующиеся определенным знаком.
Острота стереозрения, с другой стороны, хотя и представляет собой феномен весьма примечательный, но порождает проблемы технические, а не теоретические. Они относятся к третьему из введенных нами уровней, а именно к уровню механизмов реализации, поскольку в связи с остротой стереозрения возникает лишь один вопрос: сколь точно устанавливается местоположение пересечений нулевого уровня? То обстоятельство, что они могут быть локализованы с точностью до 2°, производит сильное впечатление, однако это без труда можно воспроизвести, например, в программе вычислительной машины. Необходимо просто достаточно точно определить те точки, в которых график свертки ?2 G пересекает нулевой уровень. Никаких принципиальных проблем при этом не возникает. Поразительно, что такие вычисления могут осуществляться на нейронном уровне, и, вероятно, это означает, что на каком-то этапе очень большое число маленьких клеток используется для обнаружения и локализации этих местоположений, однако процедуры не порождают теоретических проблем в том смысле, в котором их порождает стереоскопическое слияние изображений стереопары. Мы еще вернемся к проблеме остроты стереозрения в разделе, посвященном реализации на нейронном уровне.
Вергентные движения глаз и 2,5-мерный эскиз. Согласно методам, положенным в основу второго алгоритма установления соответствий между изображениями стереопары, после того, как с помощью изучения локальных окрестностей (некоторой заданной мощности) изображений, обработанных ?2 G-фильтрами, определены на них соответствия, последние помещаются во временное буферное запоминающее устройство. Эти соответствия используются также для управления движениями обоих глаз, что на основе информации, полученной на больших локальных окрестностях, дает возможность перемещать малые локальные окрестности в их области соответствия. Управление вергентными движениями глаз может осуществляться непосредственно собственно нейронами, функцией которых является установление соответствия либо косвенно с помощью буферного запоминающего устройства, либо (что наиболее вероятно) обоими способами.
Причины, позволяющие постулировать наличие памяти, можно разделить на две категории: те, которые вытекают из общего анализа предварительной обработки информации в зрительной системе, и те, которые специфически связаны с проблемой стереопсиса. Наличие какой-либо памяти, в которой может храниться нечто типа 2,5-мерного эскиза, целесообразно согласно общим положениям информационной теории зрения, поскольку она дает представление, объединяющее информацию, полученную при реализации ряда процессов предварительной обработки информации в зрительной системе. Причиной, непосредственно связанной со стереопсисом, является простота информационных процессов, обеспечивающих установление соответствий; в этом случае для хранения результатов процесса установления соответствий при изменении плоскости фиксации вследствие дизъюнктивных движений глаз и перемещении объектов в поле зрения требуется буферное запоминающее устройство. Таким образом, 2,5-мерный эскиз — это то, где в действительности происходит глобальный стереопсис: объединяются соответствия, полученные независимо по различным каналам, формируется итоговая карта значений диспаратности, которая доступна для использования другими зрительными процессами, и создается представление, составляющее основу нашего индивидуального восприятия стереограмм, воспроизводящих геометрию видимых поверхностей.
Подробное обсуждение 2,5-мерного эскиза будет приведено в следующей главе. Сейчас же мы сделаем несколько кратких замечаний относительно управления движениями глаз в стереозрении.
Дизъюнктивные движения глаз, изменяющие плоскость фиксации обоих глаз, не зависят от конъюнктивных движений глаз (Рашбасс и Уэстхаймер) и являются, скорее, плавными, чем саккадическими. Их постоянная времени равна приблизительно 160 мс, а используемая для управления ими стратегия достаточно проста. Скорость (асимптотическая) вергентных движений глаз линейно зависит от амплитуды диспаратности, причем коэффициент пропорциональности составляет около 8 град/с на градус диспаратности. Точность вергентных движений глаз доходит до 2', и при произвольных бинокулярных саккадах значения конвергенционного угла почти не изменяются. Более того, Уэстхаймер и Митчелл обнаружили, что тахистоскопическое предъявление диспаратных изображений вызывает соответствующие вергентные движения глаз, но не обеспечивает их завершения. Эти данные служат сильным аргументом в пользу того, что вергентные движения глаз осуществляются, скорее, в режиме непрерывного управления, чем баллистически.
Гипотеза заключается в том, что для управления вергентными движениями глаз используется информация о соответствиях, определяемых при использовании нескольких различных каналов с помощью описанных выше механизмов, обеспечивающих возможность приближенного восприятия глубины, и с помощью каких-то представлений границ, относящихся к более высоким уровням и участвующих в процессе непосредственно или опосредованно через 2,5-мерный эскиз. Эта гипотеза не противоречит экспериментальным данным, относящимся к стратегии и точности управления вергентными движениями глаз, и учитывает, кроме того, данные о том, что время восприятия в определенной степени зависит от распределения диспаратности на сцене. Восприятие стереограммы винтовой лестницы, поднимающейся к наблюдателю, не занимает много времени, как это происходит в случае стереограммы, представляющей две плоскости и характеризующейся тем же диапазоном изменения диспаратности, что и первая стереограмма. Исходя из нашей теории именно этого и следовало ожидать, поскольку при восприятии сцен типа винтовой лестницы, в которых значения диспаратности претерпевают гладкие изменения, имеется возможность с помощью вергентных движений глаз просматривать большие диапазоны изменения диспаратности в режиме непрерывного управления на основе выходных значений, получаемых на локальных окрестностях даже минимальной мощности. С другой стороны, стереограммы, образованные двумя плоскостями с тем же диапазоном значений диспаратности, требуют большого вергентного смещения, но не позволяют получать точную информацию, необходимую для осуществления непрерывного управления вергентными движениями глаз.
Следовательно, большое время, затрачиваемое на восприятие таких стереограмм, можно объяснить исходя из стратегии случайного поиска, используемой в системе управления вергентными движениями глаз. Другими словами, управление вергентными движениями глаз представляет собой некоторый простой непрерывный процесс с обратной связью, доступ к которому с верхних уровней обработки информации в зрительной системе обычно невозможен. Стереограммы, приведенные на рис. 3.23,
Рис. 3.23. Две стереограммы, имеющие одинаковые диапазоны изменения диспаратности: а — значения диспаратности изменяются непрерывно; б — присутствуют две диспаратные плоскости. Восприятие второй стереограммы требует большего времени, в первую очередь, вероятно, потому, что система управления вергентными движениями глаз располагает в этом случае меньшей информацией о том, каким образом следует просматривать диапазон изменения диспаратности
дают возможность читателю убедиться в том, что это, по крайней мере субъективно, действительно так.
Интересно отметить, что имеются данные, свидетельствующие о возможности научить наблюдателя совершать эффективные последовательности вергентных движений глаз. Однако этот эффект обучения связан с такой же информацией, которая используется в замкнутой системе управления вергентными движениями глаз. Априорная, вербальная и относящаяся к высшим уровням информация о стереограммах оказывается неэффективной, как, кстати очевидно, она оказывается неэффективной на всех уровнях обработки, вплоть до 2,5-мерного эскиза включительно.
↑ Реализация процесса слияния изображений стереопары на нейронном уровне
Реализация только что описанного второго алгоритма установления соответствий между изображениями стереопары на нейронном уровне еще не определена полностью. Одна из причин такого положения заключается в том, что затраты труда, необходимые для получения полного искомого описания, нельзя считать оправданными до тех пор, пока данные нейрофизиологических и психофизических исследований не дадут достаточно надежных подтверждений того, что данный алгоритм работает и вообще является правильным. Первые шаги в направлении анализа возможных нейронных механизмов, обеспечивающих реализацию ?2G-фильтра и определение пересечений нулевого уровня, тем не менее были сделаны.
Проблема бинокулярного объединения все еще остается открытой и является первой из тех, которые мы сможем сформулировать. Однако позволим себе сделать в этой связи несколько предварительных замечаний Во-первых, чувствительность к диспаратности не должна возникать прежде, чем будут обнаружены пересечения нулевого уровня. Поэтому если простые клетки поля 17 (зрительной коры), являющиеся первичными кортикальными клетками зрительного пути, чувствительны к диспаратности, как, по-видимому, имеет место у кошек, то они должны также обнаруживать пересечения нулевого уровня.
Достигаться это может различными способами, и на рис. 3.24
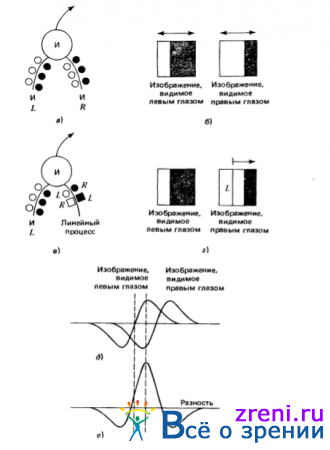
Рис. 3.24. Два возможных варианта реализации детекторов диспаратности на нейронном уровне. В первом варианте (а) нервная клетка отыскивает пересечения нулевого уровня определенного знака, используя два дендрита, каждый из которых получает информацию от своего глаза и действует независимо от другого. Результаты от каждого из денд-ритов поступают на вход логического элемента И. Таким образом, нервная клетка разряжается каждый раз, когда пересечения нулевого уровня с соответствующими знаками одновременно появляются в рецептивных полях клетки, связанных с левым и правым глазами соответственно (б). Подобная схема, однако, в состоянии обеспечить лишь довольно грубое определение значений диспаратности; к ее недостаткам, скажем, относится то, что диапазон изменения диспаратности, в котором эта схема работоспособна, варьируется в зависимости от положения пересечения нулевого уровня в рецептивном поле левого глаза. На рисунке окружности представляют возбуждающие входы, квадратики — тормозные. Незачерненные окружности и квадратики — синапсы — представляют входы, на которые поступает информация о появлении светлого раздражителя в центре рецептивного поля, зачерненные окружности и квадратики - входы, на которые поступает информация о появлении темного раздражителя в центре рецептивного поля. Символы L и R обозначают входы, на которые поступает информация от левого и правого глаз соответственно.
Вторая схема свободна от указанного недостатка, поскольку она сообщает точные данные о знаке диспаратности, но работает эта схема лишь в небольшом диапазоне изменения диспаратности. Пересечение нулевого уровня отыскивается на левом изображении с помощью дендрита И нервной клетки (в), а знак диспаратности определяется по знаку разности в точке пересечения нулевого уровня (вычисляемого с по мощью некоторого линейного процесса) значений ? 2 G-свертки для левого и правого глаз. Таким образом, эта схема представляет собой детектор знака диспаратности, не зависящий от положения пересечения нулевого уровня на изображении левого глаза, по меньшей мере в некотором небольшом диапазоне (г). При положительной указанной разности в точке пересечения нулевого уровня диспаратность имеет знак одной полярности (д), а при отрицательной - противоположной (е)
Вторая схема свободна от указанного недостатка, поскольку она сообщает точные данные о знаке диспаратности, но работает эта схема лишь в небольшом диапазоне изменения диспаратности. Пересечение нулевого уровня отыскивается на левом изображении с помощью дендрита И нервной клетки (в), а знак диспаратности определяется по знаку разности в точке пересечения нулевого уровня (вычисляемого с по мощью некоторого линейного процесса) значений ? 2 G-свертки для левого и правого глаз. Таким образом, эта схема представляет собой детектор знака диспаратности, не зависящий от положения пересечения нулевого уровня на изображении левого глаза, по меньшей мере в некотором небольшом диапазоне (г). При положительной указанной разности в точке пересечения нулевого уровня диспаратность имеет знак одной полярности (д), а при отрицательной - противоположной (е)
приведены два примера. В первом предполагается, что пересечения нулевого уровня определяются двумя дендритами независимо, и на основе локальных синаптических механизмов типа рассмотренного Поджо и Торри.
У этого механизма есть недостатки. Во-первых, он обладает не очень высокой чувствительностью к диспаратности, поскольку в каждом из глаз пересечения нулевого уровня определяются с точностью, в небольшой степени превышающей ширину центральной части рецептивного поля w1-d. Во-вторых, диапазон изменения диспаратности, на который в данном механизме обеспечивается реакция, зависит от точного положения пересечения нулевого уровня в левом глазе, так как диапазон их положений в правом глазе также фиксирован конкретной геометрией схемы его связей.
Второй пример, приведенный на рис. 3.24, представляет другой механизм. Поскольку нервная клетка управляется пересечениями нулевого уровня, поступающими от левого глаза, она является леводоминируемой. Однако разряд ее определяется разностью значений свертки для левого и правого глаз в точке пересечения нулевого уровня. Если эта разность отрицательна, диспаратность обычно будет иметь один знак, если же она положительна, диспаратность обычно будет иметь противоположный знак, как это иллюстрируется рис. 3.24. Для некоторого яркостного перехода, представляющего при движении в зрительном поле слева направо переход от светлого к темному, наличие отрицательной разности соответствует дивергентным (малая удаленность) диспаратностям. Этот второй механизм в некоторой степени устраняет неточность, свойственную первому, поскольку предусматривает непосредственное определение того, располагается ли пересечение нулевого уровня в правом глазу (его знак фиксирован), слева или справа от пересечения нулевого уровня в левом глазу. Этот механизм также имеет недостатки, однако он может оказаться ненадежным из-за слишком тесного расположения пересечений нулевого уровня или очень сильного различия контрастов в левом и правом глазах.
К сожалению, технические проблемы, связанные с нейрофизиологическими аспектами стереопсиса, существенны и объем количественных данных, которым мы располагаем сегодня, явно слишком незначителен, для того чтобы мы могли позволить себе отвергнуть любой из приведенных на рис. 3.24 механизмов либо оба. Со времени появления исходной работы Барлоу, Блейкмора и Петтигру, посвященной этой проблеме, было опубликовано сравнительно немного кривых, характеризующих чувствительность к диспаратности. Сравнительно недавно, однако, Поджо и Фискер и фон дер Хейдт с соавторами опубликовали такие должным образом проверенные кривые для обезьяны и кошки соответственно. Эти работы в целом подтверждают представление о том, что нервные клетки-детекторы диспаратности объединены в три группы, ориентированные на конвергентную, близкую к нулю и дивергентную диспаратности, причем недавно Кларк, Доналдсон и Уиттеридж обнаружили, что у овцы эти детекторы организованы в колонки, подобные тем, которые согласно гипотезе Хьюбела и Уисела должны существовать в поле 18 коры головного мозга макаки. Значения диспаратностей, правда, поразительно велики: 7° у овцы и до одного или даже нескольких угловых градусов у обезьяны. До сих пор еще не ясна конкретная роль этих детекторов в стереопсисе.
Довольно любопытно, что даже сова, пути биологической эволюции которой разошлись с путями обезьяны, возможно, раньше, чем возник стереопсис, как будто бы использует алгоритм, аналогичный алгоритму обезьяны. Петтигру и Кониси установили, что, несмотря на абсолютное отсутствие сходства анатомической организации аналога зрительной коры, имеющейся у совы, и зрительного пути обезьяны, физиологические характеристики их нервных клеток очень сходны. Однако сова не в состоянии очень много двигать глазами, и поэтому может сначала возникнуть впечатление, что она лишена возможности совершать вергентные движения глаз, столь существенные для излагаемого подхода к стереопсису. Природа тем не менее нашла выход: гороптер совы имеет наклон - он проходит через ее ноги в нижней части поля зрения и простирается вперед в бесконечность. Сова, таким образом, с помощью легких и неторопливых наклонов головы может добиться того же эффекта, который дают вергентные движения глаз, создав одновременно впечатление глубокой и сдержанной мудрости.
И наконец, существует проблема остроты стереозрения. Последняя, подобно всем остальным способностям человека к повышенной остроте восприятия, обеспечивается специальным механизмом, который позволяет выделять на изображении малые изолированные признаки с разрешением в среднем порядка 5". Крик, Марр и Поджо рассмотрели нейрофизиологические аспекты этой проблемы и высказали предположение о том, что один из возможных вариантов реализации соответствующего механизма может основываться на восстановлении с высоким разрешением изображения, подвергнутого ?2 G-фильтрации, после того как оно оказывается в зрительной коре в результате воздействия излучения в оптическом диапазоне. Барлоу высказал это предположение первым, а мы немного усовершенствовали его, указав, что восстановление не обязательно должно быть абсолютно точным. Вполне достаточно обеспечить при восстановлении участков сигнала, расположенных в окрестностях пересечений нулевого уровня, должную точность.
Естественным кандидатом на роль ’’восстановителя” изображения является популяция нервных клеток-зерен слоя IYC ? поля 17. Верхняя оценка указывает, что для каждого типа клетки (КСЦР и КТЦР) и для каждого глаза требуется не более одной нервной клетки-зерна на каждые 5" канала с наименьшим рецептивным полем. Кроме того, Д. Хьюбел отмечает, что все эти клетки обладают пространственной организацией типа ’’возбуждающий центр - тормозящая периферия”, что делает их неотделимыми от волокон коленчатого тела; взаимное расположение этих клеток к тому же отличается очень точным ретинотопическим характером - соседние нервные клетки соответствуют соседним точкам сетчатки. Очевидно, что клетки, участвующие в процессе восстановления, должны обладать всеми этими свойствами Было бы, следовательно, чрезвычайно интересно выяснить, отличаются ли их ответы в физиологическом отношении, скажем, по пространственным или особенно временным характеристикам.
↑ Определение расстояния до поверхности и ее ориентации по данным о диспаратности
Информационная теория
Расстояние от наблюдателя до поверхности. Пусть некоторая точка Р расположена на расстоянии l от левого глаза L наблюдателя и под углом ? к линии прямой видимости, как это показано на рис. 3.25.
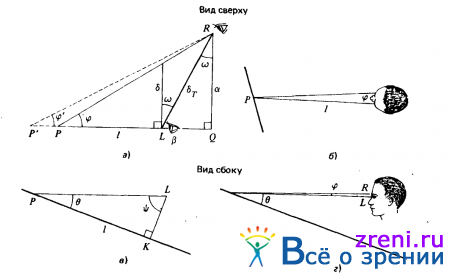
Рис. 3.25. Тригонометрические соотношения, характеризующие восстановление глубины по диспаратности. Геометрические построения в плане для случая, когда взоры обоих глаз направлены на некоторую точку Р, находящуюся на расстоянии l от левого глаза, как это показано на рис. 3.25, б (а). Линия визирования не обязательно перпендикулярна прямой, соединяющей левый (L) и правый (R) глаза; отклонение, как показано, характеризуется углом ?. Истинное расстояние между глазами равно ?T, а эффективное расстояние при данной линии визирования ?Tcos ?. Угол, образованный линиями визирования обоих глаз, обозначен через диспаратностью обычно называют разности значений углов ?, соответствующих различным точкам Р'. Отрезки ? = ?T cos ? и ? = ?Tsin ? удобно использовать в геометрических построениях, связанных с восстановлением глубины по значениям диспаратности.
Геометрические построения при боковой проекции для случая, представленного на рис. 3.25, г (б). Точка Р расположена на плоскости, наклоненной относительно горизонтальной плоскости; угол этого наклона в точке Р равен ? . На чертеже изображен только левый глаз L, и расстояние l снова указывает расстояние до точки от левого глаза. Для того чтобы определить ориентацию поверхности, необходимо восстановить значение угла ?
Геометрические построения при боковой проекции для случая, представленного на рис. 3.25, г (б). Точка Р расположена на плоскости, наклоненной относительно горизонтальной плоскости; угол этого наклона в точке Р равен ? . На чертеже изображен только левый глаз L, и расстояние l снова указывает расстояние до точки от левого глаза. Для того чтобы определить ориентацию поверхности, необходимо восстановить значение угла ?
Пусть расстояние между глазами наблюдателя равно ?Т. В таком случае, поскольку линия визирования точки Р не направлена строго вперед, эффективное расстояние между двумя глазами составляет лишь ? = ?T cos ?. Из рисунка следует, что угол ?, образованный линиями визирования правого и левого глаз, определяется как
где ? = ?T sin ?. Для малых значений угла ? можно записать следующее выражение:
Рассмотрим теперь две точки Р и Р,' расположенные на одной и той же линии визирования левого глаза, причем точка Р находится от него на расстоянии l, а точка Р' — на расстоянии l', как это показано на рис. 3.25, а и б. Отсюда следует, что диспаратность ? ? точек Р и Р' равна разности ?'-?. Если, таким образом, обозначить
то
Последнее выражение можно переписать как
Другими словами, относительное изменение расстояния при некотором определенном значении диспаратности зависит от расстояния до наблюдателя. Это обстоятельство может оказаться существенным для экспериментов, связанных с восприятием глубины, и как мы вскоре убедимся, для восприятия ориентации поверхности, поскольку оно свидетельствует о том, что при правильной работе зрительной системы человека относительное изменение воспринимаемой глубины, соответствующее некоторому определенному значению диспаратности, должно зависеть от значения расстояния l, т. е. от того, каково, по мнению наблюдателя, текущее значение истинной глубины.
Определение ориентации поверхности по данным об изменении значений диспаратности. Тригонометрические аспекты определения ориентации поверхности довольно скучны. Так как, однако, полученные в результате формулы представляют интерес, мы остановимся на них. Следует рассмотреть два случая: первый, когда наша поверхность повернута в горизонтальной плоскости (см. рис. 3.25, а и б), и второй, когда наша поверхность повернута в вертикальной плоскости (см. рис. 3.25, в и г). Это разные случаи, потому что наши глаза расположены горизонтально, а не вертикально. В обоих случаях мы хотели бы располагать формулами, связывающими ориентацию поверхности, которую мы будем характеризовать углом ?, со скоростью из менения значения диспаратности ? при изменении значения угла наблюдения ?, которую мы будем характеризовать как ??/??. Искомые формулы имеют следующий вид:
а) изменяющаяся по вертикали глубина поверхности
б) изменяющаяся по горизонтали глубина поверхности
Относительно этих формул следует сделать два замечания.
Во-первых, подобно оценкам относительной глубины, они воспроизводят зависимость от расстояния (приблизительно 1/l), с которого ведется наблюдение. Следовательно, если мозг справляется со своими задачами, то некоторая определенная скорость изменения диспаратности должна восприниматься как рост крутизны наклона поверхности по мере ее удаления от наблюдателя. Читатель может убедиться в этом, рассмотрев с различных расстояний стереограмму, приведенную на рис. 3.26.
Рис. 3.26. Обратите внимание на изменение воспринимаемой ориентации поверхности при изменении расстояния, с которого рассматривается стереограмма. Именно это явление должно наблюдаться при правильном решении зрительной системой соответствующих тригонометрических уравнений
Диспаратность и угол наблюдения изменяются одновременно, поэтому производная ??/?? постоянна при всех расстояниях, с которых ведется наблюдение. Таким образом, поверхность должна казаться все более крутой при удалении стереограммы. Так в действительности и происходит. Это свидетельствует, между прочим, и о том, что мозг достаточно хорошо информирован, где именно находится стерео грамма, и пользуется этой информацией.
Во-вторых, при скорости изменения диспаратности по горизонтали ??/??r = 1 линия визирования второго глаза должна опускаться непосредственно вдоль реальной физической поверхности или перед ней. Вторым глазом наблюдатель видит некоторое нарушение непрерывности по глубине. В этом можно убедиться, положив в формуле для изменения диспаратности по горизонтали ? = — ?, при этом ??/??r = 1. Итак, в такой ситуации полное изменение угла наблюдения первого глаза равно изменению диспаратности, так что значение производной ??/??r остается равным единице до тех пор, пока второй глаз не начнет снова осматривать поверхность. Это обстоятельство можно использовать для обнаружения нарушений непрерывности, рассматривая поверхности с некоторого расстояния при стереопсисе.
Алгоритм и его реализация
Ничего не известно относительно того, как реализуются эти формулы, хотя из примера, приведенного на рис. 3.26, следует, что приближенные варианты их воспроизведения существуют, причем точность аппроксимации может оказаться достаточно высокой. Возможно, стоит подчеркнуть, что эффекты, о которых шла речь, а именно зависимость воспринимаемой глубины и ориентации поверхности от расстояния и направления наблюдения, ни в коей мере нельзя считать неожиданными - они не относятся к разряду удивительных психофизических явлений, требующих сложных объяснений.
----
Статья из книги: Зрение | Д. Марр




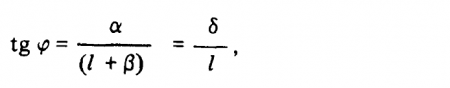
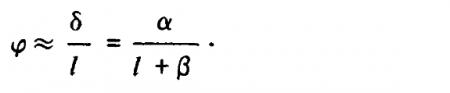

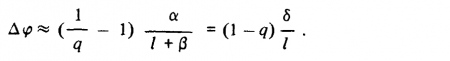
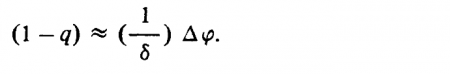
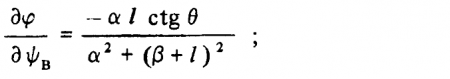

Комментариев 0