Стереопсис. Часть 1.

Описание
Мы отмечали выше, что изображения внешнего мира, формируемые каждым из глаз по отдельности, несколько отличаются друг от друга. Относительное различие положений объектов на таких изображениях называется диспаратностью, которая вызывается различиями в расстоянии до наблюдателя. Мозг человека в состоянии измерять эту диспаратность и использовать ее для оценивания относительных расстояний, отделяющих объекты от наблюдателя. Мы будем использовать термин диспаратность для обозначения угловой невязки положений изображения некоторого объекта в двух глазах, термин расстояние — для обозначения реального физического расстояния между наблюдателем и объектом, которое измеряется обычно по одному из двух глаз, термин глубина — для обозначения субъективного расстояния до объекта, определяемого восприятием наблюдателя.Наше изложение разделено на две части. Первая посвящается измерению диспаратности, вторая — использованию результатов этих измерений. В обеих частях прослеживаются три уровня. В основу данного раздела положены материалы статей по информационной теории, статьи, посвященной алгоритму, который, как предполагается, используется в зрительной системе человека, и статей, в которых описывается реализация этого алгоритма на ЭВМ. Кроме того, работы,в которых рассмотрены пересечения нулевого уровня (выполненные между 1977 и 1979 годами), позволили ввести ряд упрощений в реализацию этого алгоритма. Наиболее существенным является то, что мы чисто математически показали возможность использования рецептивных полей, обладающих круговой симметрией, вместо ориентированных рецептивных полей для выполнения исходных операций свертки. Этот же результат был независимо от нас получен с помощью методов психофизики.
Измерение стереоскопической диспаратности
Информационная теория
Процесс измерения стереоскопической диспаратности включает три шага:
1) на одном из изображений необходимо выбрать некоторую конкретнуюпозицию на поверхности, являющейся элементом изображаемой сцены;
2) на втором изображении необходимо отыскать ту же самую позицию;
3) измерить диспаратность двух соответственных точек изображения.
Если эти позиции определяются на обоих изображениях совершенно однозначно, например при выделении на исходной сцене с помощью светового луча, то необходимость в выполнении двух первых шагов отпадает и задача упрощается. В реальных условиях мы не имеем возможности аккуратно помечать поверхность сцены световым пятном, определяя затем местоположение его изображения в обоих глазах, следовательно, необходимо предусмотреть способ его установления, основанный на использовании более пассивных средств восприятия внешней среды.
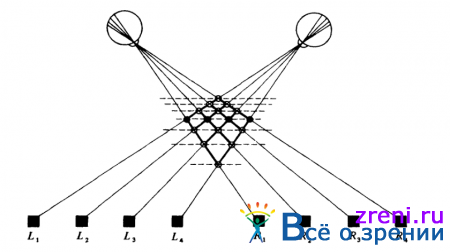
Трудность отыскания соответственных позиций на двух изображениях связана с так называемой проблемой ложной цели. Она возникает в связи с феноменом, который можно было бы определить как предельный случай предложенных Джулесом стереограмм, образованных случайными конфигурациями точек. Суть этой проблемы иллюстрирует рис. 3.5.
Рис. 3.5 Неоднозначность соответствий, устанавливаемых между двумя проекциями изображения на сетчатку. На этом рисунке каждая из четырех точек изображения, сформированного в каждом из глаз, может соответствовать любой из четырех точек проекции, сформированной в другом глазу Из этих шестнадцати допустимых соответствий лишь четыре являются истинными (они представлены зачерненными кружками); остальные двенадцать - ложные цели (незачерненные кружки) Такие неоднозначности не поддаются снятию без привлечения дополнительных ограничений, основанных на анализе глобальной информации. Предполагается, что цели (зачерненные квадратики) соответствуют элементам описания, полученным из изображений в левом и правом глазах
Вопрос состоит в том, какая точка какой соответствует. В данном примере левый глаз видит четыре точки и правый глаз видит четыре точки, однако какие из этих точек соответствуют друг другу? Вообще все шестнадцать возможных соответствий пар являются вероятными, но, рассматривая подобную стереопару, мы устанавливаем соответствия, указанные зачерненными кружками, и ни при каких обстоятельствах не устанавливаем соответствия, указанные незачерненными кружками; последние и называют ложными целями.
Хотя это в определенной степени объяснимо, тем не менее вызывает удивление. Каким образом нам удается установить, что определенные соответствия правильны, а другие следует игнорировать? Более того, существует и другое решение этой конкретной задачи установления соответствий, которое представляется столь же справедливым. Взгляните на рисунок и постарайтесь увидеть, что же на нем изображено. Альтернативным ответом служат соответствия, указанные четырьмя вертикальными точками, т. е. квадратик R1 объединяется в пару с квадратиком L4,R2 — с L3,R3 — с L2 и R4 cL1. Тем не менее зрительно мы никогда не воспринимаем установленное таким способом соответствие — мы никогда не видим это изображение как некоторый набор квадратиков, расположенных вдоль уходящей вдаль прямой. Почему же мы этого не видим? Почему мы видим лишь другой вариант, когда квадратики выстраиваются в линию, располагаясь на приблизительно одинаковом расстоянии от нас?
Читатель мог бы сразу предложить воспользоваться описаниями изображения, относящимися к высшему уровню, скажем сначала устанавливать соответствие между такими объектами, как два ряда точек в целом, затем переходить к установлению соответствий между отдельными квадратиками и, наконец, между яркостными переходами каждого квадратика. И, как я полагаю, нечто подобное имеет место, но в первую очередь необходимо ясно отдавать себе отчет в том, что такое допущение. Это, по существу, лишь некоторый механизм. На самом деле, вопрос, который следует задать, звучит следующим образом: Почему нечто подобное могло действовать? Сам по себе факт, что мы только смотрим на пару изображений, представленную на рис. 3.5, не дает никаких оснований для исключения соответствий между квадратиками L 1 и R3, L2 и R1 и даже между L3 и R1.
Нам необходимо воспользоваться какой-либо дополнительной информацией, которая помогла бы нам установить исходя из налагаемых ею некоторых ограничений, какие соответствия истинны, и для того чтобы сделать это при установлении соответствия между двумя изображениями, нам придется обращаться к изображаемому прототипу реального мира.
Необходимы следующие ограничения (на первый взгляд чрезвычайно простые) : 1) любая заданная точка реальной поверхности в любой момент времени занимает в пространстве некоторое единственное положение; 2) реальный мир целостен, он разделен на объекты, поверхности которых в общем случае гладки в том смысле, что вариации, вызванные неровностями или иными резкими переходами, которые можно трактовать как изменения расстояния между поверхностью и наблюдателем, малы по сравнению с этим расстоянием.
Эти условия отражают свойства реальных физических поверхностей, и они налагают ограничения на характер поведения некоторой точки, выбранной на поверхности. Итак, если мы намерены воспользоваться этими условиями для облегчения установления соответствия между двумя изображениями некоторой поверхности, необходимо убедиться в том, что рассматриваемые объекты находятся во взаимно однозначном соответствии с точно определенными позициями на некоторой физической поверхности. Для этого следует задать на изображении предикаты, соответствующие ’’особым приметам” поверхности, теням, нарушениям непрерывности по ориентации поверхности и т. п.
Именно исходя из подобных физических соображений мы и ввели первоначальный эскиз, именно они обеспечивают возможность использования первоначального эскиза, поскольку входящие в него элементы описания (отрезки прямых и яркостных переходов, пятна, края и нарушения непрерывности, а также характерные объекты изображения, формируемые из перечисленных элементов описания с помощью группировки и классификации) обычно соответствуют объектам, для которых на реальной поверхности существует реальный прототип. И здесь следует, вероятно, подчеркнуть, что, хотя процессы группировки и классификации должны обладать достаточной инвариантностью относительно того, что они должны группировать и классифицировать, наиболее укрупненные и обобщенные характерные объекты изображения оказываются, вообще, значительно менее надежными, чем самые предварительные и простые средства описания, входящие в необработанный первоначальный эскиз. Это обстоятельство существенно для стереопсиса, в частности, потому, что крупномасштабные характерные объекты изображения довольно велики, вплоть до нескольких угловых градусов, в то время как существенные диспаратности в общем случае достаточно невелики — порядка угловых минут. Следовательно, чем точнее должны быть измерения, тем более мелкие и простые элементы описания оказываются предпочтительными. С другой стороны, явные изменения статистических характеристик, по всей вероятности, служат вполне надежным свидетельством изменений, происходящих в реальном мире, даже на достаточно высоких уровнях и, следовательно, границы, проводимые на высших уровнях и названные мной границами разделения текстур, очевидно, для процесса стереопсиса оказываются полезнее, чем агломерации, относящиеся к тому же самому уровню. Ниже мы столкнемся с тем, что, как я считаю, является следствием этого обстоятельства.
Эти физические ограничения можно сформулировать в виде условий, определяющих установление соответствий и ограничивающих допустимые способы сопоставления двух формализованных описаний, которые построены из непроизводных элементов и относятся к одному из глаз соответственно. Для того чтобы условия соответствия выполнялись, элементы сопоставляемых описаний должны соответствовать точно определенным позициям на реальной поверхности изображаемого объекта. Можно считать, что такие элементы описания несут лишь позиционную информацию подобно черным точкам стереограмм, образованных случайными конфигурациями точек, хотя для полного изображения можно задать правила, определяющие, какие соответствия между элементами описания допустимы, а какие — нет. Эти правила выводятся и из физических соображений: если два элемента описания могут порождаться одной и той же особой приметой поверхности, между ними можно устанавливать соответствие. Если же они не могут быть порожденыодной и той же особой приметой поверхности, то устанавливать соответствие между ними нельзя. Это — первое наше условие установления соответствия, которое я буду называть условием совместимости.
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
Второе и третье условия установления соответствия отражают два физических ограничения. Условие единственности требует, чтобы каждый элемент описания, за редкими исключениями, мог соответствовать лишь одному элементу второго изображения. Указанные исключения могут возникать как следствие процесса формирования изображения, когда две особые приметы объекта расположены на линии визирования одного глаза, другим же глазом они наблюдаются отдельно. Третье условие, непрерывность, означает, что диспаратность изменяется гладко почти везде. Это условие имеет смысл, поскольку второе физическое ограничение предполагает, что расстояние от наблюдателя до видимой поверхности изменяется без нарушений непрерывности, за исключением границ объекта, которые занимают лишь малую часть площади изображения.
Итак, эти три условия служат для нас ограничениями. Теперь перейдем к их практическому использованию, высказав гипотезу, которую я буду называть основным допущением стереопсиса: если некоторое соответствие устанавливается между непроизводными элементами, допускающими физическую интерпретацию и относящимися к изображению в левом и правом глазах сцены, которая содержит достаточное число подробностей, и если это соответствие удовлетворяет трем введенным выше условиям установления соответствия, то оно правильно отражает реальное состояние наблюдаемого объекта. Из этого допущения непосредственно следует, что соответствие должно быть единственным.
Все это очень хорошо, скажет скептически настроенный читатель. Условия установления соответствия выглядят вполне обоснованными и даже весьма жесткими. Но превращать их в некое основное допущение о том, что они являются не только необходимыми следствиями физических свойств реального мира, а также на самом деле и достаточными для однозначного определения истинного соответствия, — это уже совсем другое дело.
Замечание было бы абсолютно справедливым. Оно явно и недвусмысленно указывает на одно из тех методологических положений, которые составляют основу нашего подхода. Дело в том, что введение этого основного допущения и установление его истинности — это именно то, что я подразумеваю, когда говорю об информационной теории некоторого процесса. В данном случае установить достаточность этого допущения труднее, чем установить достаточность допущения о совпадении в пространстве, поскольку последнее (весьма простое) практически непосредственно следует из структуры реального физического мира.
Тем не менее мы в состоянии подтвердить справедливость этого допущения для разнообразных ситуаций. Я попытаюсь сейчас продемонстрировать в общем виде, каким образом строится такое доказательство, так как исходное методологическое положение, к которому приводится эта проблема, исключительно важно. Мы убедимся, что оно лежит в основе теории любого процесса.
В приведенную выше формулировку основного допущения стереопсиса входят такие понятия, как ’’сцена, содержащая достаточное число подробностей” и ’’непроизводные элементы, допускающие физическую интерпретацию”, которые по математическим канонам определены чрезвычайно нестрого. Поэтому для того, чтобы избежать использования понятия ’’непроизводные элементы, допускающие физическую интерпретацию”, я введу специальный тип реальной поверхности — белую поверхность, помеченную черными точками, а для того чтобы избежать использования понятия ’’сцена, содержащая достаточное число подробностей”, я введу условие, предусматривающее довольно высокую плотность размещения точек (обозначим ее через v). В частности, для иллюстрации нашего доказательства нам потребуется, чтобы плотность v составляла по меньшей мере 2 % или что-то около того. С помощью таких несколько экзотических средств, использование которых аналогично тому, что весь видимый мир покрывается пятнышками черной краски, я преобразовываю реальную сцену в изображения, обладающие неоспоримым сходством с одной из стереограмм Джулеса, образованных случайными точечными конфигурациями. В результате условия установления соответствия задаются для двух бинарных изображений, при этом они принимают форму следующих трех правил:
Правило 1. Совместимость. Черные точки могут ставиться в соответствие только черным точкам.
Правило 2. Единственность. Почти всегда некоторой черной точке одного изображения можно поставить в соответствие не более одной черной точки другого изображения.
Правило 3.Непрерывность. Изменение диспаратности установленных соответствий на изображении гладко почти везде.
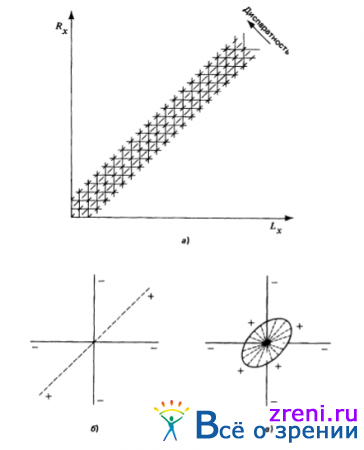
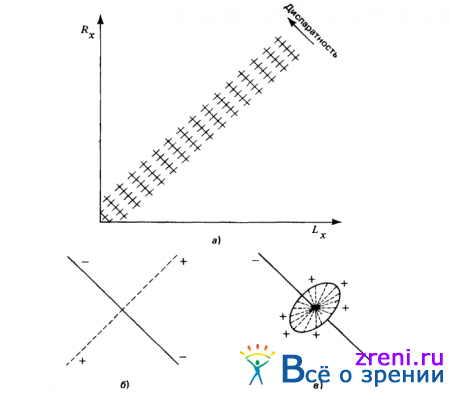
Теперь наша задача доказать, что эти три правила обеспечивают установление взаимно однозначного соответствия двух изображений, а сделать это мы можем следующим образом. Во-первых, заметим, что, поскольку глаза расположены горизонтально, нам следует учитывать только те допустимые соответствия, которые расположены вдоль горизонтальных прямых; следовательно, задача может быть сведена к простому одномерному случаю, проиллюстрированному рис. 3.6, а.
Рис. 3.6. Lx и Rx — координаты, характеризующие положение элементов описания на левом и правом изображениях (а). Сплошные вертикальные и горизонтальные отрезки прямых представляют линии визирования левого и правого глаз. Их пересечения соответствуют допустимым значениям диспаратности. Штриховые диагональные прямые обозначают линии постоянной диспаратности.
Кооперативный алгоритм, описываемый в тексте, предусматривает размещение ячейки в каждом узле сети; в этом смысле сплошные прямые представляют тормозящие связи, а штриховые — возбуждающие. Локальная структура произвольного узла сети на рис. 3.6, а приведена на рис. 3.6, б. Этот алгоритм допускает обобщение на двухмерный случай - при этом локальная структура произвольного узла соответствующей сети будет иметь вид, показанный на рис. 3.6, в. Изображенный на нем овал представляет плоский диск, поднимающийся из плоскости страницы
Кооперативный алгоритм, описываемый в тексте, предусматривает размещение ячейки в каждом узле сети; в этом смысле сплошные прямые представляют тормозящие связи, а штриховые — возбуждающие. Локальная структура произвольного узла сети на рис. 3.6, а приведена на рис. 3.6, б. Этот алгоритм допускает обобщение на двухмерный случай - при этом локальная структура произвольного узла соответствующей сети будет иметь вид, показанный на рис. 3.6, в. Изображенный на нем овал представляет плоский диск, поднимающийся из плоскости страницы
На этом рисунке через Lx обозначены все допустимые координаты точек на сетчатке левого глаза, а через Rx — все допустимые координаты точек на сетчатке правого глаза. Непрерывные вертикальные и горизонтальные отрезки прямых представляют линии визирования левого и правого глаз соответственно; штриховые диагональные прямые обозначают перемещения с постоянной скоростью по изображениям левого и правого глаз, т. е. плоскости постоянной диспаратности.
Выполнить доказательство теперь не составит труда, по крайней мере в концептуальном отношении. Правило 1 указывает, что рассматривать следует только черные точки. Правило 3 говорит о том, что истинные соответствия в целом сосредоточиваются на этих диагоналях или вблизи от них, а правило 2 — что в каждой отдельной точке следует выбирать лишь те соответствия, которые располагаются на этих плоскостях постоянной диспаратности. Плотность расположения точек на каждом изображении равна v, так что плотность допустимых соответствий на истинной плоскости постоянной диспаратности также равна ?. в то время как на остальных (’’неистинных”) плоскостях постоянной диспаратности она составляет лишь ?2. Следовательно, эти три правила обеспечат получение единственного решения при условии, что диспаратность изменяется достаточно медленно, чтобы площадь А, приходящаяся на каждую плоскость постоянной диспаратности, была достаточно велика и значение A ? существенно отличалось от значений A ?2. Итак, поскольку решение единственно (определяется A ?—соответствиями), оно правильно отражает физическую реальность, поскольку в этом случае может быть получено только одно решение. Именно это является главным моментом доказательства. Конечно, такая формулировка несколько примитивна и целый ряд деталей требует специального рассмотрения.
Доводы, приведенные нами, подтверждают следующие два положения. Во-первых, основное допущение стереопсиса справедливо, и справедливо потому, что входящие в него условия сформулированы на основе доводов, отражающих структуру реального физического мира. И, во-вторых, основное допущение стереопсиса обеспечивает надежный фундамент для определения процесса установления соответствия, так как всякое соответствие, удовлетворяющее этому допущению, с гарантией является истинным. Более того, в обычных реальных ситуациях такое соответствие всегда можно установить. На этом изложение информационной теории стереопсиса заканчивается.
Алгоритмы для установления соответствий между изображениями стереопары
Кооперативный алгоритм. В подтверждение того положения, что для реализации некоторого процесса можно предложить не один, а несколько различных алгоритмов, мы приведем два алгоритма, обеспечивающих установление соответствий между изображениями стереопары. Первый естественно следует из анализа, проведенного в предыдущем разделе: иллюстрации, представленные на рис. 3.6, облегчат понимание принципа действия этого алгоритма.
Как было показано выше, правила 2 и 3 определяют решение задачи установления соответствий. Правило 2, в сущности, сводится к тому, что вдоль каждого из горизонтальных и вертикальных отрезков на рис. 3.6, а допускается установление лишь одного соответствия. Правило 3 указывает, что истинные соответствия проявляют тенденцию к расположению по штриховым диагоналям.
Сейчас мы займемся построением параллельной сети взаимосвязанных процессоров, обеспечивающей непосредственную реализацию этих двух правил. В каждое пересечение - узел (см. рис. 3.6, а) — помещается маленький процессор. Идея состоит в том, что узлу, представляющему истинное соответствие пары черных точек, должно быть приписано в конечном счете значение ”1”. Если же вершина не представляет истинного соединения — ложная цель, как мы назвали ее выше, — то процессор должен выдавать значение ”0”.
Для реализации наших правил используются связи, устанавливаемые между процессорами. Как нам известно, правило 2 утверждает, что вдоль каждой горизонтальной или вертикальной прямой можно устанавливать лишь одно соответствие. Поэтому все процессоры, расположенные в узлах каждой вертикальной или горизонтальной прямой, должны блокировать друг друга. В результате конкуренции, возникающей на каждой из прямых, лишь один процессор сможет воспроизводить единицу, а все остальные - только нули, и, следовательно, правило 2 будет выполняться. Правило 3 утверждает, что истинные соответствия обычно располагаются вдоль пунктирных прямых, поэтому по таким направлениям мы вводим между процессорами возбуждающие связи. В результате структура каждого локального процессора принимает вид, приведенный на рис. 3.6, б. От каждого локального процессора тормозящие (блокирующие) связи направляются к процессорам, расположенным вдоль горизонтальной и вертикальной прямых, приведенных на этом рисунке и соответствующих линиям визирования обоих глаз, а возбуждающие связи направляются вдоль диагонали, представляющей собой линию постоянной диспаратности. Этот алгоритм можно даже обобщить на двухмерный случай - при этом тормозящие связи остаются без изменений, а возбуждающие покрывают некоторую небольшую двухмерную окрестность, в которой диспаратность постоянна. Этот вариант показан на рис. 3.6, в.
Настраивается эта сеть следующим образом: рассматриваются два изображения, и значение ”1” присваивается всем допустимым парам черных точек, для которых вообще могло бы быть установлено соответствие - ложным целям и всем до единой допустимым парам; остальным же узлам сети присваивается значение ”0”. После этого сеть начинает работать. Для каждого процессора суммируются единицы, которыми помечены его возбуждающие связи, и отдельно суммируются единицы, которыми помечены его тормозящие связи; далее полученные значения вычитаются одно из другого (после того, как одна из сумм умножается на соответствующий весовой коэффициент). Если результат вычитания превышает некоторую пороговую величину, процессору присваивается значение ”1”, в противном случае ’’0” Формально этот алгоритм можно записать с помощью следующего итерационного соотношения:
где Cx ;d обозначает состояние ячейки сети, представленной на рис. 3.6. а (состояние ячейки, местоположение которой определяется координатами (х, у), в момент времени t; d - соответствующее значение диспаратности); S (х, у, d) — локальная возбуждающая окрестность и 0(х, у, d) - тормозящая окрестность; 6 — некоторая постоянная торможения, а ? — некоторая пороговая функция. Начальное состояние С0 включает все допустимые соответствия, в том числе ложные цели, в пределах заданного диапазона значений диспаратности В данном случае оно учитывается на каждом шаге итерации (это не необходимо, но алгоритм при этом сходится быстрее). Обратите внимание на то, каким образом геометрическая организация тормозящих и возбуждающих окрестностей О и S обеспечивает реализацию правил 2 и 3.
Этот алгоритм позволяет успешно обрабатывать стереопрограммы, образованные случайными конфигурациями точек. На рис. 3.7
Рис. 3.7. Расшифровка стереоскопической пары изображения, образованных случайными конфигурациями точек, с помощью кооперативного алгоритма. Стереоскопическая пара изображений (стереограммы) помещена в верхней части рисунка; исходное состояние сети, включающее все допустимые соответствия в пределах заданного диапазона значений диспаратности, обозначено меткой ”0”. Алгоритм выполняет ряд итераций (результаты некоторых из них представлены на рисунке), постепенно выявляя искомую структуру. Различные уровни зачерненности изображения соответствуют различным значениям диспаратности
показано, как такая сеть с помощью последовательной самоорганизации обеспечивает воспроизведение правильного решения. На рисунке приведены левая и правая стереограммы, начальное состояние сети обозначено через ”0”, а состояние сети после выполнения п итераций - соответствующим числом Для того чтобы понять, каким образом эти рисунки отображают состояние сети, следует предположить, что наша сеть рассматривается сверху, т. е. точка наблюдения расположена в верхней части рис. 3.6. Слои сети, соответствующие разным значениям диспаратности, располагаются в параллельных плоскостях, так что наблюдатель смотрит сквозь них вниз. Часть узлов, расположенных в каждой из этих параллельных плоскостей, возбуждена, а часть - заторможена. Каждому из семи слоев сети приписывается отдельный уровень серого тона, и поэтому некоторый возбужденный узел, принадлежащий верхнему слою (соответствующему диспаратности, составляющей +3 пиксела), вводит в изображение черную точку, а некоторый возбужденный узел, принадлежащий самому нижнему слою (соответствующему диспаратности, составляющей -3 пиксела), вводит в изображение белую точку. В начальном состоянии (нулевая итерация) сеть неорганизованна, конечное же ее состояние соответствует устойчивой упорядоченности (14-я итерация); в результате обнажается структура, напоминающая перевернутый свадебный торт. Плотность заполнения стереограммы точками в данном случае составляет 50 %.
Алгоритм, заданный приведенным выше итерационным соотношением, можно применять для расшифровки стереограмм, образованных случайными конфигурациями точек с плотностью заполнения от 50 до менее 10 %, взяв в качестве значений параметров те же, что использовались в примере на рис. 3.7. При таких и меньших плотностях заполнения сходимость алгоритма уменьшается. Если допустить возможность использования какого-либо простого геометрического механизма для управления зависимостью пороговой функции а от усредненной активности сети (числа возбужденных ячеек) на каждой итерации, то данный алгоритм оказался бы пригоден для расшифровки стереограмм с очень низкой плотностью заполнения точками. В нашем втором примере, который приведен на рис. 3.8,
Рис. 3.8. Алгоритм, применение которого проиллюстрировано рис. 3.7, можно также использовать для расшифровки и заполнения чрезвычайно слабозаполненных стереограмм. На данном рисунке плотность заполнения составляет 5 %
плотность заполнения стереограммы точками составляет 5 % и значение диспаратности центрального квадрата относительно фона составляет -2 пиксела. Алгоритм обеспечивает заполнение областей, в которых не имеется ни одной точки, но при этом для получения решений, подобных тем, что мы имеем при плотности заполнения 50 %, требуется выполнить на несколько итераций больше. Рассматривая слабозаполненные стереограммы, мы воспринимаем контуры четче, чем это делает алгоритм. Это, вероятно, объясняется тем, что между точками, расположенными на границах объектов, возникают субъективные контуры.
Эти параметры способствуют интуитивному пониманию работы алгоритма. Судя по всему, он ”не испытывает никаких затруднений” при обработке стереограмм, но одного этого обстоятельства недостаточно, для того чтобы считать его надежным. Нам, однако, удалось придать ему интеллектуальную респектабельность: проанализировав математические свойства этого алгоритма, мы показали, что состояния, удовлетворяющие условиям правил 2 и 3, являются устойчивыми состояниями алгоритма, и продемонстрировали сходимость алгоритма в широком диапазоне значений его параметров.
Мы рассмотрели пример кооперативного алгоритма, названного так из-за использованного в нем способа достижения глобального результата с помощью хорошо отрегулированной ’’кооперации” локальных операций. Кооперативные явления хорошо известны в физике, скажем предложенная Изингом модель ферромагнетизма, сверхпроводимость и фазовые переходы. Кооперативные алгоритмы обладают многими общими с этими явлениями свойствами.
Кооперативные алгоритмы и задача установления соответствия между изображениями стереопары. Вплоть до 1977 года почти все стереоалгоритмы, представляемые как модели, ориентированные на процесс стереопсиса у человека, основывались на гипотезе Джулеса о том, что процесс установления соответствия между изображениями стереопары — это некоторое кооперативное явление. Два исключения составляют программа AUTOMAP Джулеса, в основу которой положен метод, предусматривающий выделение кластеров, и модель Сперлинга, основанная на корреляции уровней серого тона, но вносящая интересный вклад в изучение связи стереопсиса с вергентными движениями глаз.
Анализ всех этих работ приводит к одному весьма примечательному выводу: не считая нашего алгоритма, в основу которого положен информационный подход, ни одно описание указанных алгоритмов не сопровождается анализом соответствующих информационных аспектов задачи установления соответствия между изображениями стереопары. Непосредственным следствием этого обстоятельства является то, что ни один из алгоритмов не дает верного результата, так как, по меньшей мере одно из условий основного допущения стереопсиса либо не учитывается, либо неправильно реализовывается. Модель Сперлинга основана на корреляции уровней серого тона, что, как мы убедились, неверно и из-за чего эта модель не реализована. Сперлингу не удалось определить размеры и расположение окрестностей, на которых должна осуществляться корреляция. Именно в связи с этим и возникают проблемы.
Алгоритм Дев заслуживает внимания как одна из первых попыток точного претворения в жизнь идей Джулеса. В этом алгоритме реализованы правила 2 и 3, однако первое из них - в неправильной модификации. Вместо двух тормозящих связей, по одной на каждую линию визирования, Дев использовала в своем алгоритме одну тормозящую связь, разделяющую пополам угол между линиями левого и правого глаз. Этот алгоритм, который иллюстрирует рис. 3.9,
Рис. 3.9. В некоторых из известных кооперативных стереоалгоритмов предусматривается использование только одного набора тормозящих связей между детекторами, соответствующими различным значениям диспаратности и относящимися к одной и той же позиции сетчатки. Если представить эти связи в том же, что и на рис. 3.6, виде, становится очевидно, что они воспроизводят иные ограничения: вместо запрещения установления двух соответствий на каждой линии визирования, как это было в случае, представленном на рис. 3.6, эти связи запрещают установление двух соответствий по любому радиусу, исходящему из позиции, занимаемой наблюдателем. Такой способ организации процесса установления соответствий между изображениями стереопары неверен
следует сопоставить с геометрической организацией, представленной на рис. 3.6. Физически соединения, показанные на рис. 3.9, соответствуют некоторому варианту правила, утверждающего, что наблюдатель, куда бы он ни направлял взгляд, увидит только одну поверхность. Вообще говоря, это неверно: когда Вы смотрите, например, на неглубокое озеро, Вы видите две поверхности - поверхность озера и его дно. В правильном варианте (см. рис. 3.6) такое правило гласит, что любые заметные характерные особенности находятся либо на поверхности озера, либо на его дне (либо, возможно, на теле какой-то рыбы, плавающей на озере), но обязательно лишь на одной из этих поверхностей.
В алгоритме Сугиэ и Сувы частично реализовано правило 3 и использована все та же неверная модификация правила 2. Нелсон не предложил никакого варианта алгоритма и не воплотил своих идей, однако он, очевидно, также имел в виду некоторый алгоритм, использующий неправильную модификацию правила 2. Хираи и Фукусима правильно использовали правило 2 , но отказались от использования правила 3, предпочтя ему сеть, ’’благосклонную” к решениям, соответствующим меньшим значениям параллакса.
Джулесу в своей программе AUTOMAP не удалось реализовать правило 2, но правило 3 в ней неявно используется для выделения кластеров. Больший интерес вызывает дипольная модель Джулеса. Она представляет собой физическую аналоговую модель, в которой для представления левого и правого изображений стереопары используются две сетки (по одной на каждое изображение), образованные магнитными стрелками (магнитными диполями); для каждой характерной особенности каждого изображения, подлежащей установлению соответствия, в сетке предусмотрена отдельная магнитная стрелка. Ориентация стрелок такова, «то при наложении двух таких сеток они могут располагаться острием в направлении соседних позиций сетки, представляющей второе изображение. В каждой из сеток концы соседних стрелок соединены пружинками, и полярность каждой магнитной стрелки (северная или южная) выбирается в соответствии с яркостью изображения (черное или белое) в этой позиции. Идея, положенная в основу такой модели, состоит в том, что при приближенном установлении соответствий с помощью наложения сеток, представляющих левое и правое изображения, магнитное притяжение, которое возникает между аналогично расположенными группами стрелок, приведет к стабилизации каждой сетки; в результате стрелки каждой сетки будут указывать на правильно соответствующие им стрелки второй сетки. Хотя соотношение полярностей магнитиков и значений яркостей сетчатки неизвестны, за исключением 'случая стереограмм, образованных случайными конфигурациями точек, в дипольной модели в неявном виде реализована единственность, т. е правило 2, поскольку в любой момент времени некоторый определенный диполь может иметь лишь одну ориентацию. Соединение кончиков соседних диполей пружинкой обеспечивает реализацию условия непрерывности правила 3. Данная модель, следовательно, в наибольшей степени удовлетворяет нашим требованиям, однако в отличие от других кооперативных моделей не представляет в явном виде всех допустимых узлов структуры, приведенной на рис. 3.6, а. В сущности, в данном случае на каждый вертикальный и горизонтальный отрезки этой структуры приходится лишь по одному процессору, а отдельным узлам, расположенным на них, соответствуют различные углы, под которыми располагается этот единственный диполь. Было бы интересно узнать, может ли такая модель работать.
Затронул же я эту тему лишь для того, чтобы подкрепить свой общий тезис, состоящий в том, что интеллектуальная строгость используемого метода имеет решающее значение при изучении возможностей обработки информации зрительной системой. Если информационная основа некоторого процесса сформулирована неверно, то соответствующий алгоритм почти наверняка окажется неверным.
И наконец, ни для одного из упоминавшихся алгоритмов не была продемонстрирована возможность работы с естественными изображениями. Механизм корреляции уровней серого тона обладает определенной работоспособностью, однако при его использовании возникают ошибки, исправлять которые должен человек-оператор. Что касается других методов, то для них не определен вид входного представления, хотя следует отметить, что Марр и Поджо указывали на пригодность использования в качестве такого представления первоначального эскиза.
Биологические данные. Все обсуждавшиеся в предыдущем разделе алгоритмы предназначены для выбора правильных соответствий в тех случаях, когда ложных целей очень много. Поэтому, за исключением, быть может, первых вариантов дипольной модели Джулеса, ни в одном из них движения глаз не учитываются, гак как вообще они дают возможность интерпретировать стереограммы, образованные случайными конфигурациями точек без учета этих движений. Движения глаз человека, однако, представляются существенными для стереоскопического зрения человека. На самом деле, без таких движений человек может воспринимать лишь очень небольшую глубину - область, в которой достижимо слияние двух изображений (ее называют фузионной зоной Панума порядка 6 - 18'), что почти полностью исключает возможность восприятия любых структур, за исключением случаев малых значений диспаратности. Для сложных стереограмм типа спирали Джулеса движения глаз, возможно, оказываются существенными и чрезвычайно удивительно, что, несмотря на известные старые результаты Фендера и Джулеса, психофизики до недавнего времени уделяли так мало внимания движениям глаз.
Известно еще несколько психофизических явлений, которые было бы трудно объяснить с помощью рассмотренных нами алгоритмов. Некоторые люди, например, в состоянии справляться с ситуациями, когда одно из изображений увеличивается в размерах на 15 %. Это, однако, всего лишь наиболее яркая демонстрация явления, которое может проявляться и по-другому. На самом деле, человек может одновременно воспринимать бинокулярное ’’соревнование” и слияние отдельных составляющих спектра стереограммы, в чем читатель может убедиться, обратившись к рис 3.10.
Рис. 3.10. Высокочастотные компоненты спектра этой стереограммы находятся в состоянии ’’соревнования" в отличие от низкочастотных, которые могут достигать слияния. В этом случае следует предположить, что в процессе стереопсиса участвуют независимые каналы, настраиваемые на различные значения пространственных частот
Подобные наблюдения приводят к очень интересной гипотезе на определенном этапе обработки зрительной информации передача информации, характеризующей диспаратность, производится по специальным каналам стереопсиса, настраиваемым на различные частоты и перекрывающим приблизительно полторы октавы (эти каналы, в сущности, очень сильно напоминают операторы ?2G с рецептивными полями различных размеров).
Среди других представляющих интерес результатов следует отметить физиологические, клинические и психофизические данные, относящиеся к гипотезе Ричардса о двух группах. Основной результат Ричардса состоит в том, что стереослепота проявляется как ’’слепота” относительно любых конвергентных диспаратностей, любых дивергентных диспаратностей или относительно и тех и других. Кстати, различные стереоаномалии распространены чрезвычайно широко, охватывая до 30 % людей. Другими словами, стереодетекторы организованы, очевидно, в две группы, одна из которых должна обеспечивать восприятие конвергентных, а другая — дивергентных диспаратностей, причем, возможно, существует и третья группа, предназначенная для восприятия нулевой диспаратности. Данные нейрофизиологов свидетельствуют приблизительно то же самое - существуют, грубо говоря, три класса нейронов, настраиваемых на определенную диспаратность класс, настраиваемый на конвергентную диспаратность (так называемые нейроны малой удаленности), класс, настраиваемый на дивергентную диспаратность (так называемые нейроны большой удаленности), и третий класс, настраиваемый на близкие к нулю значения диспаратности. Диапазоны значений диспаратности, на которые настраиваются нейроны первых двух классов, достаточно велики, в то время как нейроны третьего класса характеризуются острой настройкой. Эти данные противоречат представлению реализации рассмотренных выше алгоритмов на нейронном уровне, поскольку, не считая дипольной модели, все они предусматривают использование большого числа ’’нейронов-детекторов диспаратности”, максимальная чувствительность которых перекрывает значительно больший диапазон значений диспаратности, чем обеспечивают кривые настройки отдельных нейронов
И наконец, еще одно замечание, касающееся причин, побудивших нас обратиться к подходу, который предусматривает использование кооперативных алгоритмов. Как мы уже отмечали, все реализованные в нем идеи возникли под влиянием одного результата Фендера и Джулеса - демонстрации наличия явления гистерезиса в процессе стереопсиса. В своих экспериментах они стабилизировали изображение относительно движений глаз и показали, что при условии возникновения слияния двух изображений их можно ’’раздвигать” без нарушения слияния вплоть до значения диспаратности порядка 2° Если же, однако, слияние нарушается, то для его восстановления необходимо снова начать совмещение изображений, вернув их в область 6 — 14'. Гистерезис является одной из особенностей кооперативных алгоритмов, и поэтому заполнение промежутков также, очевидно, проявляется в процессе стереопсиса (как читатель уже имел возможность убедиться, стереограммы с малой плотностью заполнения, подобные приведенной на рис 3.8, воспринимаются как некоторая гладкая твердая поверхность, а не как несколько отдельных точек, подвешенных в пространстве). Исходя из этого все, в том числе Джулес и мы, обратились к кооперативному алгоритму.
Для подобного шага тем не менее не было особых оснований. В конечном счете, важнейшим результатом данного эксперимента Фендера и Джулеса было подтверждение наличия гистерезиса при значениях диспаратности порядка двух градусов, в то время как соответствие устанавливается при 20'. Следовательно, представляется маловероятным возникновение гистерезиса как результата процесса установления соответствий и значительно более вероятным, что его можно приписать работе корковой памяти, запоминающей результаты, получаемые при установлении соответствия, но действующей независимо от последнего процесса. Фендер и Джулес даже выступили с такой гипотезой. Конечно, это не исключает возможности использования механизма кооперативности в процессе установления соответствия, и так называемый эффект распространения, описанный позже Джулесом и Чаном, служит, очевидно, подтверждением его наличия. Вывод же, однако, состоит в том, что не следует, возможно, придавать такое значение нашим представлениям, связанным с кооперативными процессами, и целесообразно обратиться к совсем иному подходу к проблеме стереопсиса.
Второй алгоритм. Основная проблема, которую приходится решать при достижении бинокулярного слияния, — это устранение ложных целей или разработка способа, обеспечивающего возможность их не рассматривать. Сложность этой проблемы определяется двумя факторами: изобилием на изображении признаков, подходящих для использования в процессе установления соответствия, и диапазоном значений диспаратности, в пределах которого последний процесс разворачивается. Если какой-либо признак встречается на изображении достаточно редко, то в процессе установления соответствия может оказаться просмотренным достаточно большой диапазон значений диспаратности, прежде чем поиск приведет к встрече с ложной целью, если же, однако, признак является стандартным либо критерий, используемый при установлении соответствия, определен не очень точно, то ложные цели могут встречаться уже при просмотре совсем небольшого диапазона значений диспаратности.
В таком случае для упрощения задачи установления соответствий следует уменьшить ’’область определения” признаков, подходящих для использования в процессе установления соответствий, т. е. необходимо сделать признаки редкими событиями. Добиться этого можно двумя способами. Первый — сделать их очень сложными или придать им чрезвычайно специфический вид, с тем чтобы даже при высокой плотности их распределения на изображении число их разновидностей оказалось бы столь велико, что сопоставимая пара возникала бы редко. Второй способ состоит в значительном уменьшении плотности распределения на изображении всех признаков, скажем, с помощью понижения степени пространственного разрешения при изучении изображения.
Из работы Джулеса, посвященной стереограммам, образованным случайными конфигурациями точек, известно, что перспективы первого подхода весьма проблематичны. Мы знаем, что установление соответствия — локальная процедура, если все яркостные переходы строго вертикальны или горизонтальны и имеют один и тот же контраст, и, следовательно, использование даже очень специфических критериев не очень поможет нам. Более того, это привело бы к существенному ухудшению результатов при работе с реальными изображениями, у которых ориентации и контрасты двух соответствующих друг другу яркостных переходов могут поразительным образом отличаться. Читатель, обратившись к рис. 3.11,
Рис. 3.11. Несмотря на то, что контрастности левого и правого изображений различны, их слияние все же оказывается возможным
сам может убедиться в том, что стереограммы с различными контрастностями поддаются слиянию. Контрасты, однако, должны иметь один и тот же знак. Критерии ориентации также весьма нестроги.
Более перспективным, однако, представляется другой способ. Действительно, тот факт, что при бинокулярном слиянии используются независимые каналы, настраиваемые на различные пространственные частоты, снова привлекает к себе внимание, представая в совершенно новом свете, поскольку это означает, что при слиянии используются несколько вариантов одного и того же изображения, получаемых с помощью последовательного уточнения фильтрации. В результате обеспечивается увеличение разрешения по диспаратности и в конечном счете - достижение очень высокой степени такого разрешения за счет уменьшения диапазона значений диспаратности.
Примечательным свойством любой системы, реализующей указанные механизмы, является использование движений глаз при построении подробной и точной карты диспаратностей для двух точек наблюдения. Дело в том, что наиболее точные значения диспаратности дают каналы высокого разрешения и, следовательно, становятся существенны движения глаз, так как каждая часть сцены должна в конечном счете попасть в тот малый диапазон значений диспаратности, в котором действуют эти каналы высокого разрешения. Важность вергентных движений глаз связана также и с тем, что этими движениями можно управлять с высокой точностью.
Такие данные позволяют предложить следующую схему для решения задачи слияния: 1) каждое изображение анализируется с помощью каналов, характеризующихся различной точностью, и соответствия устанавливаются между результатами, полученными в каналах одинаковой точности по каждому из обоих глаз для значений диспаратности, соответствующих порядку разрешения канала; 2) каналы с малым разрешением управляют вергентными движениями глаз, обеспечивая синхронизацию работы точных каналов.
В этой схеме отсутствует гистерезис и, следовательно, не учитываются результаты Фендера и Джулеса. С другой стороны, согласно развиваемой нами теории промежуточного уровня обработки информации в зрительной системе основной целью нижнего уровня обработки зрительной информации является построение своего рода карты ориентаций-глубин для всех поверхностей, которые доступны взору наблюдателя. Она объединяет данные, полученные с помощью ряда различных и, очевидно, независимых процессов, которые позволяют интерпретировать информацию, заключенную в диспаратности, движении, тенях, текстуре и контурах. На рис. 3.12
Рис. 3.12. Иллюстрация понятия 2,5-мерного эскиза. На рис. 3.12, а изображены в перспективе маленькие квадратики, характеризующиеся различными ориентациями относительно наблюдателя. Точки со стрелками условно представляют ориентации этих поверхностей. На рис. 3.12, б это же условное представление использовано для указания ориентаций двух цилиндрических поверхностей, расположенных на перпендикулярном к наблюдателю фоне. Полный 2,5-мерный эскиз должен включать приближенные значения расстояний до поверхностей, а также их ориентации, контуры, на которых ориентации поверхности претерпевают резкие изменения (эти контуры изображены точками), и контуры, на которых происходит нарушение непрерывности по глубине (субъективные контуры, они изображены сплошными линиями).
приведено представление, реализующее идею такой карты и названное Марром и Нисихарой 2,5-мерным эскизом.
Предположим теперь, что гистерезис, обнаруженный Фендером и Джулесом, возникает нe в результате некоторого кооперативного процесса, действующего при установлении соответствий изображений стереопары, а является следствием использования некоторого буферного запоминающего устройства типа 2,5-мерного эскиза для хранения карты глубин изображения после того, как она построена. В таком случае процесс установления соответствий не должен обязательно носить кооперативный характер (даже если он еще мог бы быть таковым) - необязательно даже, чтобы при этом процесс установления соответствий реализовывался на всем изображении одновременно, если карта глубин видимой поверхности построена и введена в указанное промежуточное запоминающее устройство
Мы можем теперь завершить построение своей схемы, добавив к ней следующие два этапа: 3) после того как некоторое соответствие установлено, оно фиксируется и включается в 2,5-мерный эскиз; 4) существует некоторая разновидность обратной связи между запоминающим устройством и каналами, проявляющейся в управлении движениями глаз, которое дает наблюдателю возможность легко подвергать слиянию любой участок поверхности при условии, что карта ее глубин введена в запоминающее устройство.
Идея начать процесс с установления соответствий для затрубленных и сильно разнесенных признаков, а затем, используя полученную таким образом информацию, повторять этот процесс при более высоких уровнях разрешения выглядит многообещающе, однако какие признаки следует сопоставлять при этих различных уровнях разрешения? Нам известно достаточно много о предварительном этапе обработки зрительной информации, для того чтобы иметь возможность предлагать различные варианты. Следует ли обратиться к пересечениям нулевого уровня, необработанному первоначальному эскизу, полному первоначальному эскизу, или целесообразно использовать какую-нибудь комбинацию этих представлений? Поджо и я предложили, что исходное представление для процесса установления соответствий между изображениями стереопары должно включать необработанные пересечения нулевого уровня, снабженные указаниями о знаке изменения контраста и их приближенной ориентации на изображении, и концы (локальные нарушения непрерывности), также снабженные указаниями о контрасте и, возможно, об очень приближенных значениях ориентации.
Продолжение в следующей статье: Стереопсис. Часть 2.
----
Статья из книги: Зрение | Д. Марр


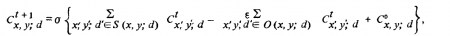




Комментариев 0