Световая чувствительность

Содержание:
Описание
↑ Основы фотометрии
Основное свойство рецепторов сетчатки — световая чувствительность, т. е. способность, поглощая свет, инициировать первую ступень сложного зрительного процесса. Чувствительность фоторецепторов к свету чрезвычайно велика: рецептор способен генерировать импульс возбуждения при поглощении всего нескольких, быть может только двух, фотонов. Но вероятность того, что фотон будет поглощен светочувствительным веществом рецептора, в сильной степени зависит от энергии фотона, т. е. от частоты или длины волны излучения. Зависимость вероятности поглощения фотона от длины его волны лежит в основе световой фотометрии, обуславливая способ пересчета энергетических величин в световые, прежде всего мощности излучения Р (Вт) в световой поток Ф (лм). Первые фотометрические измерения, еще в XVIII в. проводились при достаточной освещенности, когда хорошо различаются цвета, т. е. когда работают колбочки. Поэтому основные фотометрические величины были установлены для дневного, колбочкового зрения. В основу была положена единица силы света — свеча. Сначала это была просто свеча типа восковой или стеариновой, потом старались обусловить материал и диаметр свечи, затем воспроизводили эталон в виде пламенной лампы с определенными конструкционными ее параметрами (свеча Гефнера). В двадцатом веке световые эталоны были созданы в виде ламп накаливании. Во второй половине нашего столетия в основу эталона силы света было положено излучение черного тела при температуре затвердевания платины. Сила света одного квадратного сантиметра черного тела при температуре 2042 К принята равной 60 свечам или по современной терминологии 60 канделам (60 кд). Устройство первичного светового эталона достаточно сложно.
В целях его лучшей сохранности и упрощения поверочных испытаний создают вторичные и рабочие световые эталоны. Их изготовляют из специально отобранных и отожженных ламп накаливания. Прямым сравнением с первичным эталоном определяют световые характеристики вторичных эталонов, по которым поверяют рабочие эталоны. В практике лабораторных фотометрических измерений пользуются образцовыми светоизмерительными лампами, которые время от времени сравнивают с рабочими эталонами, хранящимися в метрологических учреждениях. Схема сравнения с первичным эталоном изображена на рис. 19.
Рис. 19. Сравнение силы света лампы накаливании с эталоном
Кварцевый сосуд 2 засыпан окисью тория 1, в которую погружен тигель 4 с трубкой 5 из плавленой окиси тория. Тигель наполнен химически чистой платиной 3, поддерживаемой при температуре 2042 К. Излучение выходит из печи через смотровое окно 6 и с помощью призмы 7 и объектива 8 через диафрагму 9 направляется на пластинку 10, которая освещается с другой стороны вторичным эталоном в виде лампы накаливания 11. Свет, рассеянный обеими сторонами пластинки, направляется в фотометрический кубик 12. Смотря на него в окуляр, наблюдатель видит картину, изображенную на рис. 20.
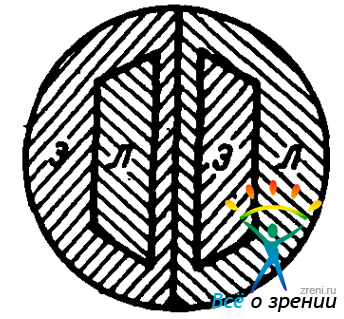
Рис. 20. Распределение яркости, создаваемое фотометрическим кубиком
Поля, обозначенные буквой 3, освещены светом первичного эталона, а буквой Л — лампы накаливания. Передвигая лампу 11, наблюдатель на некотором расстоянии l между пластинкой 10 и лампой 11 добивается одинаковой яркости полей. Яркости обеих сторон пластинки пропорциональны их освещенностям, а так как материал и обработка обеих сторон пластинки одинаковы, коэффициенты пропорциональности между яркостью и освещенностью в обоих случаях равны. Поэтому можно написать уравнение
где Jэ и Jл — сила света первичного и вторичного эталонов; коэффициент а учитывает преобразование пучка света от первичного эталона объективом 8 и потери в призме 7 и объективе 5; ?с — коэффициент пропускания системы двух призм фотометра, сквозь которые свет проходит после рассеяния на пластинке 10.
Таким образом, можно найти силу вторичного эталона
Следует обратить внимание на то, что хотя здесь измеряется сила света, непосредственно в фотометре уравниваются яркости двух полей. Силу света получают уже путем расчета. Это обстоятельство характерно для всей визуальной фотометрии: глаз может сравнивать только яркости и при измерениях работает как нуль-прибор. Равенство яркостей в хороших условиях мы можем устанавливать с большой точностью, с погрешностью меньшей одного процента. Но попытки определить, во сколько раз одна яркость превосходит другую, приводят к очень большим ошибкам.
Положив в основу световых величин силу света и установив ее единицу — канделу, мы можем дальше строить всю систему фотометрических световых величин и единиц. Единица светового потока — люмен. Равномерный точечный источник с силой света 1 кд излучает в телесном угле 1 ср световой поток 1 лм. Между силой света J и потоком Ф источника в этом случае существует соотношение
Освещенность измеряется потоком, приходящимся на единицу площади:
Единица освещенности — люкс (лк), равный одному люмену, приходящемуся на квадратный метр, лм/м2.
Яркость светящейся поверхности в направлении нормали к ней измеряется отношением силы света этой поверхности к ее площади.
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
Освещенный белый экран, обладающий равномерно-диффузным отражением с коэффициентом отражения р, приобретает яркость, которую можно подсчитать по формуле
↑ Спектральная чувствительность
В быту мы оцениваем силу света источника по его мощности. Мы знаем, что стоваттная лампочка дает больше света, чем двадцатипятиваттная. Но оценка силы света по мощности возможна только для источников одного типа. Электроплитка с открытой спиралью тоже светит. Но каждый знает, что шестисотваттная плитка светит гораздо хуже, чем двадцатипятиваттная лампочка. Из-за низкой температуры плитки почти всю энергию она излучает в инфракрасной области и только немного — в длинноволновом диапазоне видимых лучей. И все же можно сказать, что световой поток источника пропорционален его мощности, но коэффициент пропорциональности зависит от спектрального состава излучения. Чтобы внести ясность в соотношение между световым потоком и мощностью, нужно обратиться сначала к монохроматическим излучениям, т. е. к излучениям, длины волн которых заключены в узком интервале d?. Тогда мы сможем написать формулу
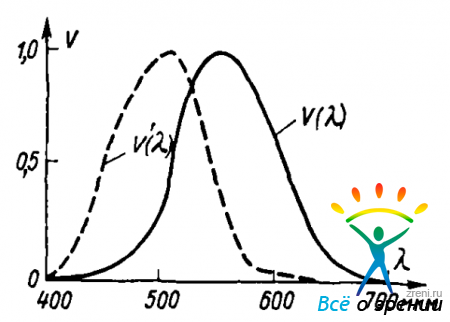
где dФ — световой поток, приходящийся на узкую спектральную область d?; Р? — спектральная плотность мощности, т. е. dP/d?; Кm — максимальная спектральная световая эффективность, равная 683 лм/Вт; V(?) —относительная спектральная световая эффективность излучения для дневного зрения. Эту безразмерную величину часто называют устарелым, но лаконичным и удобным названием — относительная вндность. Эта величина характеризует чувствительность глаза к свету различных длин волн. Каждой длине волны ? соответствует одно значение V(?). Наглядное представление о функции V(?) может дать такая процедура ее определения.
Рядом поставлены два белых экрана, площади которых равны. На первый экран посылают излучение мощностью 1 Вт с длиной волны ?1 = 555 нм (желто-зеленый свет), а на второй — другое излучение, скажем зеленое, с длиной волны ?2 = 500 нм. Если его мощность будет тоже 1 Вт, мы увидим, что второй экран много темнее первого. Чтобы уравнять яркости, мощность второго излучения придется увеличить до 3 Вт. Значит, чувствительность глаза к излучению ?2 составляет одну треть чувствительности к излучению ?1 Приняв чувствительность к ?1 = 555 нм (она максимальна) за единицу, получим, что чувствительность к свету с длиной волны ?2 = 500 нм равна 1/3 (точное значение V(?) =0,323). Таким же образом мы можем найти V(?) для всех других длин волн и получить зависимость К(Х) в виде таблицы или графика. Можно найти и значение коэффициента Кm. Мощность излучения, лежащего в узком интервале длин волн АХ, выразим в виде
а соответствующий световой поток будет
Послав этот поток на экран площадью Аа, обладающий свойствами, обеспечивающими выполнение равенства (31), получим его яркость, воспользовавшись формулами (29), (31) и (34):
Если теперь непосредственно измерить L, то в формуле (35) будут известны все величины, кроме Кm, откуда
В действительности определение V(?) и Кm — весьма сложная задача, во-первых, в силу необходимости производить гетерохромное фотометрирование, т. е. уравнивать по яркости поля разного цвета, а во вторых, из-за индивидуальных различий в спектральной чувствительности.
На основе анализа экспериментальных работ Международная комиссия по освещению утвердила значения относительной спектральной эффективности для стандартного фотометрического наблюдателя МКО. На базе этих значений построена основная система фотометрирования. На основе утвержденных МКО значений V(?) построена кривая, изображенная на рис. 21 (сплошная линия).
Рис. 21. График функции V (?)
Подведем некоторые итоги.
Свет, как всякий материальный объект, обладает массой и энергией. Поэтому фотометрию можно строить как учение об энергии света, кладя в основу мощность излучения. Такая фотометрия действительно существует, и ею рассматриваются чисто энергетические величины: энергетическая сила света, мощность или поток излучения, энергетическая освещенность, энергетическая яркость. Для измерений в области энергетической фотометрии лучше всего подходят неселективные приемники, прежде всего тепловые, обращающие в тепловую энергию излучения любой длины волны. Но для такой важной отрасли науки и практической деятельности, как светотехника, чисто энергетическая фотометрия неудобна. Для светотехника важно учитывать воздействие света на селективный приемник — глаз человека. Так, еще раньше энергетической фотометрии появилась ее частная отрасль — визуальная фотометрия с системой световых единиц — световой поток, освещенность, яркость.
Световой поток — это мощность излучения, оцениваемая по ее действию на глаз. Следует еще добавить — на глаз, адаптированный к высоким уровням яркости, когда приемником света служат колбочки (дневное зрение). Можно подумать, что в световые величины вводится элемент субъективности. Оценка по действию на глаз... На чей глаз? Однако после регламентации значений функции относительной видности субъективность исчезает.
Световой поток (а следовательно, и все другие световые величины) становится объективной физической величиной, определяемой формулой (32) и стандартизованными значениями V(?) и Кm. Чтобы от спектрального потока в интервале длин волн перейти к потоку Ф, следует проинтегрировать (32) в пределах от нуля до бесконечности.
Интеграл всегда сходится, так как вне сравнительно узкой области видимого спектра V(?) =0. Практически вполне достаточно брать интеграл в пределах от 380 до 760 нм.
Если бы фотометрия строилась не исторически, а логически, формулы ее можно было бы упростить. Первоначальная независимость визуальной фотометрии от энергетики вызвала необходимость введения коэффициента Кm, который позднее пришлось определять экспериментально. Можно было бы положить Кm = 1, это упростило бы соотношения между энергетическими и световыми величинами.
↑ Эффект Пуркинье
При значительном понижении уровня яркости, с наступлением ночи восприятие света переходит к палочкам, спектральная чувствительность которых сильно отличается от чувствительности колбочек. На связанное с таким различием явление более полутораста лет тому назад обратил внимание чешский ученый, доктор и профессор медицины Ян Пуркинье. Эффект Пуркинье заключается в том, что в сумерках предметы красного цвета становятся темнее синих, а зеленые становятся синеватыми, так как теряют желтую составляющую их цвета. Ночью, когда цвета уже совсем не различаются, алая роза кажется темнее василька.
Уже сам Пуркинье дал в общих чертах правильное объяснение открытому им явлению. Гельмгольц получил уже некоторые количественные результаты, характеризующие смещение максимума спектральной чувствительности в сторону более коротких волн при понижении яркости.
Хотя изучению явлений, связанных с эффектом Пуркинье, посвящено довольно много работ (хороший обзор их дан в книге А. А. Волькенштейна), долгое время казалось, что они представляют интерес только для физиологов. Считалось, что активная деятельность человека при малых яркостях составляет по времени примерно сотую часть всей работы человека. Однако Бертлинг справедливо заметил, что хотя чаще всего работает светлоадаптированный глаз, те более редкие случаи, когда приходится полагаться на ночное или сумеречное зрение, бывают наиболее критическими, так что ошибка в расчете освещения может иметь роковые последствия. В тридцатых годах нашего столетия возникли новые задачи освещения наружных пространств газосветными лампами, в связи с чем стала очевидной необходимость уточнения светотехнических расчетов в области малых освещенностей. В начале столетия к увеличению экономичности ламп накаливания был один основной путь — увеличение температуры нити ламп. Это было выгодно для светлоадаптированного глаза и тем более для темноадаптированного. Появление газосветных и люминесцентных ламп разорвало термодинамическую связь между температурой и спектром излучения. Получили распространение, например, натриевые лампы, отличающиеся большой световой отдачей. Однако, в силу эффекта Пуркинье это их преимущество теряет силу при освещенностях в доли люкса. Еще Бертлинг сравнил экономичность нескольких ламп при высокой и низкой освещенности, в частности натриевой и ртутной ламп, световая отдача которых при высокой освещенности составляла соответственно 51 и 33 лм/Вт. Оказалось, что при низкой освещенности натриевая лампа даст в 6 раз меньше света на ватт потребляемой мощности, чем ртутная
Изучению работы зрения при низких освещенностях и связанных с этим фотометрических и светотехнических вопросов посвятили свои работы многие ученые, как советские, так и зарубежные. Назовем имена хотя бы некоторых из них: С. О. Майзель, А. А. Гершуи, Н. И. Пинегин, В. Г. Самсонова, С. Г. Юров, А. А. Волькенштейн, Боума, Стайлс, Кроуфорд, Уолд.
В результате Международной комиссией но освещению была стандартизована относительная спектральная световая эффективность излучения для ночного зрения V'(?), кривая которой проведена на рис. 21 штриховой линией. Максимум V'(? приходится на длину волны 507 нм.
Международный светотехнический словарь рекомендует считать дневным (фотопическим) зрением работу глаза, адаптированного к уровням яркости по меньшей мере в несколько кд/м2, а ночным (скотопическим) — работу глаза, адаптированного к яркостям, меньшим нескольких сотых кд/м2.
↑ Эквивалентная яркость
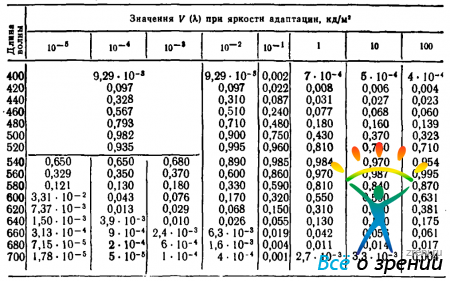
При фотопическом зрении работают только колбочки, при скотопическом — только палочки. Однако остается еще несколько порядков значений яркости, при которой в зрительном процессе участвуют и колбочки, и палочки. Это область сумеречного (мезопического) зрения. Пришлось исследовать функции видности и в промежуточной зоне. В табл. 4
Таблица 4. Относительная спектральная световая эффективность излучения V(?) в зависимости от яркости адаптации
приведены восемь функций видности в интервале яркости 10_5 кд/м2 —до 100 кд/м2.
После того как была обнаружена зависимость спектральной чувствительности от яркости, Л. А. Гершун предложил для ее учета кроме стандартной (фотопической) яркости ввести новую величину — эквивалентную яркость Lеq. Эта величина официально принята МКО, термин 45-10-085
Яркость, выраженную через световой поток, в определение которого входит функция V(?) [формула (36)], называют фотопической или стандартной. Эквивалентную яркость поверхности, освещенной излучением любого спектрального состава, условились измерять, визуально уравнивая ее с яркостью белой поверхности, освещенной излучением черного тела при температуре затвердевания платины (2042 К). Назовем такое излучение эталонным. Создаваемая эталонным излучением стандартная яркость при любых ее уровнях считается численно равной эквивалентной яркости. Для излучения любой иной цветовой температуры это равенство стандартной и эквивалентной яркостей нарушается при низких уровнях освещения, где вступает в силу эффект Пуркинье. Поясним сказанное примером.
Пусть одно поле фотометра — назовем его первым — освещено эталонным излучением, причем освещенность его можно изменять в любое число раз, сохраняя неизменным спектральный состав света. Осветим второе поле лампой накаливания с температурой нити 2800 К и установим на обоих полях фотометра яркость 100 кд/м2. Уменьшим теперь освещенность обоих полей в 100 000 раз. Стандартная яркость их станет 10-3 кд/м2. Но мы ясно увидим, что второе поле светлее первого. Чтобы сделать поля равиосветлыми, стандартную яркость первого поля придется увеличить примерно до 1,4 X 10-3 кд/м2. Это и будет эквивалентной яркостью второго поля, стандартная яркость которого равна 10_3 кд/м2. Разница объясняется тем. что излучение более высокой цветовой температуры, спектр которого сдвинут в сторону коротких волн, меньше проигрывает в светлоте при переходе к палочковому приемнику, максимум чувствительности которого сдвинут в ту же сторону.
Фотометр для измерения эквивалентных яркостей должен иметь большое поле зрения (не меньше 25°) и большой выходной зрачок (не меньше 7,5 мм в диаметре). Поля сравнения лучше делать концентрическими: внутреннее 14°, внешнее до 25—30°. Измерения проводят при установившемся состоянии адаптации.
Система эквивалентных яркостей находит применение в научных исследованиях функций зрения при малоярких цветных полях и в практической светотехнике, например при установлении весьма низких норм цветного (красного) освещения в цехах, производящих или обрабатывающих светочувствительные материалы.
Методы вычисления эквивалентной яркости приведены в книге Волькенштейна. Если источник света можно достаточно точно характеризовать цветовой температурой Тц, применима приближенная формула, предложенная Кинни
↑ Пороговая яркость
Абсолютная световая чувствительность глаза характеризуется пороговой яркостью Ln. Чем меньше Ln, тем больше световая чувствительность Sc.
Чему же равна пороговая яркость? Несмотря на многочисленные исследования, ответить на этот вопрос не так легко. Во-первых, из-за того, что Ln сильно зависит от условий наблюдения, например от площади тестового поля. Во-вторых, из-за того, что четкие представления об эквивалентной яркости вошли в фотометрию сравнительно недавно и при использовании литературных данных не всегда известно, какую яркость имел в виду автор. А если и ясно, что речь идет о стандартной яркости, редко имеется достаточно данных, чтобы пересчитать ее в эквивалентную. Однако порядок величины L,, указать можно. Кнппп для поля диаметром 2°, излучающего свет с длиной волны ?. = 555 нм. получил Leq = 5,1 • 10-6 кд/м2 (стандартная яркость L = 2,1 X 10-6 кд/м2). По данным Луриа для темноадаптированного глаза при больших размерах тестового пятна (от 8 до 100° в диаметре) пороговое значение эквивалентной яркости Leq лежит в пределах от 0,3 • 10_6 до 0,7 • 10_6 кд/м2.
Можно согласиться с В. В. Мешковым и принять, что пороговая яркость равна одной миллионной кд/м2. Часто фон с яркостью L = 10_6 кд/м2 считают совершенно темным, полагая, что дальнейшее уменьшение яркости не влияет на функции зрения: даже яркость, на порядок большая, т. е. 10-5 кд/м2, обеспечивает скотопическое зрение, которому соответствует функция V(?).
При определении пороговой яркости в глаз входит довольно большой световой поток соответственно большой площади тестового поля. Уменьшение поля приводит к уменьшению воспринимаемого потока. Поэтому минимальный световой поток, еще способный вызывать ощущение света, следует определять по наблюдению точечных источников. Если же требуется определить минимальную порцию световой энергии, воспринимаемой зрением, нужно ограничить длительность воздействия света на сетчатку, т. е. наблюдать короткие вспышки точечного источника.
Какой источник считается точечным? Типичный точечный источник — звезда. Диаметры звезд измеряются малыми долями секунды. Однако вследствие дифракции и аберраций на сетчатке звезда изображается пятном с диаметром, не меньшим одной угловой минуты. Поэтому точечным можно считать любой источник, угловой диаметр которого не превышает минуты.
Пока мы имеем дело с протяженными источниками, для глаза важна их яркость, которая в конечном счете определяет освещенность изображения источника на сетчатке Е'. В самом деле, пусть источник имеет форму квадрата, сторона которого равна у. Глаз наблюдателя находится на нормали к плоскости квадрата, на расстоянии l от него. Силу света источника в направлении нормали найдем по формуле
где L — яркость в направлении нормали. Тогда освещенность Е на роговице глаза будет
а поток, достигший сетчатки
где ?r — коэффициент пропускания глазных сред; d — диаметр зрачка глаза.
Поток Ф осветит на сетчатке площадь ?' (площадь изображения источника), которая равна у'2. А так как у' по формуле (12) равен —?f, то
Освещенность на сетчатке получим, разделив Ф' на ?' и приняв во внимание, что угловой размер объекта ? = y/l:
Видим, что в формулу Е' не входит расстояние до светящейся поверхности. Объект (самосветящийся или получивший яркость L в результате рассеяния света других источников) кажется нам одинаково ярким на расстоянии и 2, и 5, и 20 м. Яркость протяженного объекта не зависит от его углового размера ?.
Но положение меняется, если ? становится меньше одной минуты. Здесь теряет смысл формула (42), ?' делается практически постоянной величиной и освещенность изображения точечного источника оказывается пропорциональной потоку Ф, который в свою очередь пропорционален освещенности Е на поверхности зрачка наблюдателя [формула (40)]. Подставив в формулу (40), в числитель силу света J по формуле (39), получим
Освещенность Е, создаваемая точечным источником на зрачке наблюдателя, называется блеском источника. Именно блеск, изменяясь обратно пропорционально квадрату расстояния от источника, определяет видимость звезды. Минимальная освещенность на зрачке, при которой мы еще видим источник, называется пороговым блеском. Будем обозначать пороговый блеск для периферического зрения Еn, а для центрального Eц.
Литературные данные хотя и не вполне совпадают, но не расходятся по порядку величины. На основе иx анализа мы даем округленные значения порогового блеска в полной темноте, т. е. при яркости фона L = 10-6 кд/м2 или меньшей, при бинокулярном наблюдении: En = 2*10-9 лк; Eц = 2*10-8 лк.
Поскольку колбочки концентрируются в центральной части сетчатки, а палочки преобладают на периферии, Eц можно считать порогом колбочковой чувствительности, а Еn — палочковой. Случается, что человек, заметив далекий огонь периферическим зрением, поворачивает к нему глаза и теряет его. Астрономы даже говорят, что для того чтобы видеть слабую звезду, не надо на нее смотреть.
↑ Квантовый порог чувствительности
Определим теперь минимальную световую энергию, которая может обусловить зрительное восприятие. Световая энергия Qv при ее постоянстве во времени выражается произведением светового потока Ф и времени его действия т:
Пороговое значение световой энергии получим по формуле
где Фn — пороговый поток, входящий в глаз при блеске En; ? — время инерции зрения, т. е. время, в течение которого глаз суммирует воздействие света. При темновой адаптации ? = 0,2 с.
Для вычисления Фn положим, что диаметр зрачка d = 0,8 см = 8-10-3м, и умножим Еn на площадь зрачка ?d2/4. Получим Фn = 10-13 лм и QVn = 2-10-14 лм*с. Тем же путем получим пороговый поток и пороговую световую энергию для центрального зрения: Фц = 10-12 лм и Qvц = 2-10-18 лм*с. Примерно такие же значения Qvn и Qvц мы получим, если будем исходить из данных работы, в которых непосредственно определялось произведение Ец? или Еn? при малых т.
Оценим энергию Qn и Qц, входящую в зрачок при пороговом восприятии соответственно периферическим и центральным зрением. Для перехода от световой величины Qv к энергетической Q умножим обе части формулы (33) на ? и, учитывая, что ??Ф = ?QV, а ??Р = ?Q, получим
Будем производить вычисление для монохроматического света с длиной волны ?, соответствующей максимуму спектральной эффективности, т. е. для периферии ? = 507 нм, а для центрального зрения ? = 555 нм. Тогда V(?) = 1 и мы сможем написать Q = Qv/Km. Отсюда Qn = 1,5*10-17Дж = 1,5-10-10 эрг; Qц = 1,5*10-16 Дж = 1,5*10-9 эрг.
Энергия фотона q = hc/?, где h — постоянная Планка, а с — скорость света. Разделив Qn и Qц на соответствующие значения q, получим числа фотонов, входящих в зрачок при пороговом восприятии света периферическим и центральным зрением, nп = 39 и nц = 424.
Пропускание глазных сред зависит от длины волны: для ? = 507 нм тг = 0,б1; для ? = 565 нм ?r = 0,57. Значит, число фотонов, доходящих до сетчатки, n'п = 20; n'ц = 242. Только часть дошедших до сетчатки фотонов поглощается молекулами светочувствительного вещества, вызывая их возбуждение. Назовем такое поглощение активным поглощением и введем величину a1 — коэффициент активного поглощения монохроматического света, соответствующего максимуму спектральной световой эффективности. По данным Вавилова при темновой адаптации a1 = 0,22. Хехт дает несколько меньшее число, Роуз считает, что а, лежит в пределах от 0,1 до 0,2, т. е. a1n'п = 2/4. Итак, чтобы наблюдатель заметил световую вспышку, палочки его сетчатки должны активно поглотить от двух до четырех фотонов. Для колбочек а1 раз в десять меньше, чем для палочек. Но число активно поглощенных фотонов на пороге восприятия и для колбочек, по-видимому, лежит в тех же пределах.
----
Статья из книги: Глаз и свет | Луизов А.В.




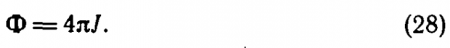



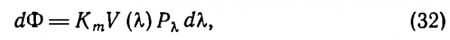




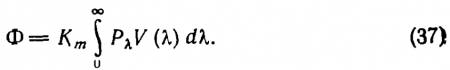
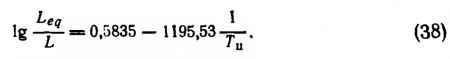









Комментариев 0