Зрительный процесс

Описание

↑ Введение

Пожалуй, нигде соперничество между физикой и биологией не проявляется столь ярко, как в зрительном процессе. Природа с самого начала была поставлена в жесткие условия, ибо свет передается конечными порциями энергии, называемыми «фотонами» или «квантами». Любая информация, которую требовалось извлечь из окружающего мира, оказывалась ограниченной в силу дискретной природы света.

В течение миллионов лет эволюции стремление выжить было доминирующим мотивом существования всех многообразных живых организмов. Жизнь обрывалась, если жертве не удавалось вовремя заметить преследователя. Зрение, служило не только основным, но и почти единственным способом обнаружить врага. Оно должно было действовать и в сумерках и даже при свете звезд, когда энергия света поступает лишь редкими порциями. Было поистине делом жизни и смерти — собрать и использовать каждый фотон, чтобы лучше увидеть надвигающуюся опасность. Здесь требовалось устройство, не уступающее счетчику фотонов.

Простейшие формы жизни дают нам достаточные свидетельства того, что природа давно овладела искусством счета фотонов. Если бы проблема заключалась только в использовании энергии падающих фотонов, то мы могли бы обратиться к эпохе, предшествующей появлению животных, и указать на осуществляемый растениями фотосинтез как на пример эффективного преобразования энергии. Однако счет фотонов — это не только их эффективное поглощение, но и весьма сложный процесс усиления. Энергия фотона достаточна для возбуждения только одного атома или одной молекулы. При использовании лишь этой энергии информация о поглощении фотона не могла бы быть передана за пределы точки поглощения, и тем более не достигла бы центральной нервной системы. Нервный импульс представляет собой движение, по крайней мере, нескольких миллионов атомов или ионов. Следовательно, энергия поглощенного фотона должна быть усилена в миллионы раз, прежде чем она сможет вызвать нервный импульс. Замечательный усилитель, созданный для этого природой, до сих пор остается загадкой. Огромному разнообразию усилителей, разработанных для той же цели человеком, и посвящена значительная часть данной книги.

Квантовый характер света создает жесткие ограничения. Природа не могла сделать в физическом смысле больше, а в смысле выживания — меньше, чем создать счетчик фотонов. Располагая таким счетчиком, можно было решить и второй вопрос — как обращаться с получаемой информацией.

Например, падающие фотоны могут накапливаться либо в течение долгого времени — это дает высококачественное изображение, либо за короткие интервалы времени — тогда получается последовательность быстро меняющихся изображений низкого качества. При долговременном накоплении движущиеся объекты казались бы расплывшимися. Более того, животному пришлось бы замедлять движение для того, чтобы во время экспозиции его «камера» (то есть зрительная система) не смещалась. Во втором же случае чрезвычайно малое время экспозиции привело бы к изображениям столь низкого качества или столь обедненным информацией, что их ценность для управления поведением животного была бы невелика. Природа нашла разумный компромисс, по крайней мере в том, что касается человека, — она «установила» время экспозиции, соответствующее времени реакции человеческой системы в целом. Последнее складывается из -времени прохождения нервных импульсов от глаза к мозгу и обратно к соответствующей конечности, а также времени, необходимого для преодоления физической (точнее, механической) инерции этой конечности. В общей сложности время реакции оказывается порядка десятой доли секунды, как и продолжительность экспозиции глаза.

«Выбор» времени экспозиции, так же как и выбор области спектральной чувствительности, легко понять; последняя имеет максимум вблизи максимума спектрального распределения солнечного излучения — и в сумерках даже смещается в голубую область в соответствии с изменением спектрального состава света, рассеянного «голубым» небом. Не менее удачно «выбраны» и другие, возможно не столь очевидные, характеристики зрительной системы, изучая которые в настоящем мы можем лучше понять прошлое. Сюда относятся диаметр зрачка и его фокусное расстояние, красная и голубая границы видимой области, плотность элементов сетчатки, которая определяет верхний предел качества изображения, число измерений в системе цветового зрения, запрограммированные взаимосвязи между волокнами зрительного нерва и, наконец, даже количество и расположение глаз. Позднее мы вернемся к этому вопросу и приведем некоторые примеры адаптации оптических параметров в соответствии с образом жизни ряда животных. Пока мы лишь укажем на существенное различие между проблемой счета фотонов — первоосновной, исключительной и необходимой— и разнообразными способами, с помощью которых счет фотонов был приспособлен к образу жизни определенных животных и которые, безусловно, носят вторичный характер.

↑ Ограничения зрительного процесса, связанные с квантовой природой света

Абсолютной мерой качества зрительной системы служит отношение информации, пропущенной этой системой, к информации, содержащейся в падающем потоке света и попадающей в систему. Поэтому необходимо иметь количественную меру информации, переносимой конечным числом фотонов. Мы введем такую меру в несколько этапов, что поможет нам выделить три стороны ограничения зрительного процесса, обусловленные квантовой природой света.

Первая связана с дискретностью световых квантов;
Вторая — с их хаотическим распределением во времени и пространстве;
Третья относится к проблеме распознавания ложных сигналов, то есть ложных зрительных образов, которые могут быть обусловлены хаотическим характером распределения фотонов, а не самим объектом.

Вследствие этих ограничений для передачи элемента информации требуется значительно большее число фотонов.

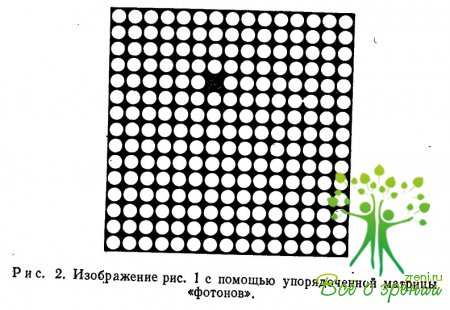
Дискретность световых квантов. Представим себе черный холст, на котором мы хотим изобразить белую стену с одним черным пятном на ней (рис. 1).

Наше изображение будет предельно простым — мы лишь покажем наличие черного пятна на белой стене, не вдаваясь в тонкости его структуры. «Технику» живописи мы сведем к рисованию пунктиром. Мы можем изобразить множество маленьких белых точек одинакового размера, но расположенных на различных расстояниях друг от друга. Каждая белая точка будет соответствовать зрительному эффекту, производимому одним фотоном в некой обобщенной зрительной системе.

Предположим, что размер черного пятна таков, что на холсте при плотном расположении умещается в общей сложности N пятен. Тогда одно черное пятно соответствует элементу картины,
площадь которого составляет N ^-1 часть холста.

Возникает вопрос: какое наименьшее число белых точек требуется для изображения одного черного пятна на однородно белой стене? Если располагать белые точки равномерно, то очевидно, что для
заполнения холста N-1 белых точек будет как необходимо, так и достаточно. Единственная недостающая белая точка указывает место, где находится одно черное пятно (рис. 2).

Теперь несколько усложним технику живописи: изобразим одно серое пятно, указав степень его серости. Предположим, что коэффициент отражения пятна составляет 99% такового для белой стены., и вновь зададимся вопросом о наименьшем числе белых точек, необходимых для передачи информации. Очевидно, для этого требуется 100 N-1 точек. Каждый элемент картины содержит в точности 100 точек, за исключением одного элемента, представляющего собой серое пятно. В последнем находится 99 точек, это означает, что его яркость составляет 99% яркости окружающей стены.

Все вышесказанное чрезвычайно элементарно, однако проведенное рассуждение показывает, что для изображения малых элементов с низким контрастом требуется много фотонов. Например, для получения изображений с хорошим разрешением число элементов картины должно лежать в пределах 10 ⁶-10 ⁷. Следовательно, для того чтобы указать местоположение и яркость серого пятна, нам требуется
примерно 10 ⁸-10 ⁹ фотонов . Точнее, нам потребовались бы эти 100 N фотонов, если бы их можно было расположить вполне регулярно — по 100 фотонов на элемент картины. Но природа работает не столь упорядоченным образом. Фотоны хаотически падают в разные точки и в разные моменты времени, что приводит к неизбежной зернистости любого изображения — зернистости, которая затрудняет различение мелких деталей и слабых контрастов. В результате число фотонов, требуемое для передачи мелких деталей изображения, значительно возрастает.

Хаотический характер распределения фотонов. Естественный некогерентный свет излучается, если существует электронное возбуждение, например возбуждение атомов. Среднее время жизни возбужденного состояния — совершенно определенный, поддающийся расчету и измерению параметр. С другой стороны, фундаментальное свойство такой квантовомеханической возбужденной системы состоит в том, что фотон может быть испущен в любой момент в течение среднего времени жизни возбужденного состояния. Точнее, вероятность испускания фотона в пределах интервала времени ?t вблизи произвольного момента времени I выражается как ехр(—t/?)?t/?, где ? — среднее время .жизни возбужденного состояния. Для нашего рассмотрения существенно то, что эмиссия фотонов представляет собой стохастический процесс.
[banner_centerrs] {banner_centerrs} [/banner_centerrs]

Проведем простой эксперимент: осветим небольшую площадку, например, лампочкой накаливания, дающей «постоянную» интенсивность, и будем подсчитывать число фотонов, попадающих на площадку в течение данного времени ?t. Мы получим набор чисел n ₁ , n ₂ ,..., соответствующих истинному числу фотонов, падающих в течение первого интервала ?t., второго интервала ?t. и т. д. Слово «постоянный» мы взяли в кавычки, поскольку наш эксперимент служит одним из способов выяснения того, имеет ли источник в самом деле постоянную интенсивность. Различие в значениях чисел n ₁ , n ₂ ... может поставить под сомнение постоянство интенсивности источника. Однако сколь бы тщательно мы ни контролировали источник, окажется, что разброс в числах неустраним. Этот разброс является следствием стохастического, или случайного, характера процесса испускания фотонов.

В частности, если среднее число фотонов, попадающих на исследуемую площадку,
равно n ₀ , то числа n ₁ , n ₂ будут распределены вокруг n ₀ таким образом, что среднее значение выражения (n _i - n ₀ )² окажется равным n₀. Средняя величина (n _i - n ₀ )² называется дисперсией. Квадратный корень из этой величины, или ((n _i - n ₀ )²)^? , называется среднеквадратичным отклонением (ошибкой).

Введем термины, которые в дальнейшем мы будем часто использовать. Сигнал определяется как среднее число фотонов, падающих на тестовую элементарную площадку, а шум — как среднеквадратичное отклонение от этого числа. В вышеприведенном примере n₀ представляет собой величину сигнала, а — n₀^? величину шума. Тогда отношение сигнал/шум также равно n₀^? Под термином «сигнал» мы будем понимать разность между средними числами фотонов, падающих на тестовый элемент и окружающие его элементарные площадки того же размера. В этом смысле данный термин мы будем, например, использовать для обозначения сигнала, относящегося к расположенному на однородном фоне низкоконтрастному тестовому элементу.

Вернемся теперь к черному холсту, на котором мы хотим изобразить серое пятно с помощью белых точек, каждая из которых соответствует фотону. Согласно нашей первой оценке, сделанной в случае однородно распределенных точек, для изображения одного серого пятна, яркость которого составляет 99% яркости окружающего холста, нам требуется 100 точек на элемент картины (элемент картины мы определили как площадь серого пятна). Если учесть случайный характер распределения фотонов, то окажется, что в действительности числа фотонов, падающих на площадки различных элементов картины, распределены вокруг среднего значения (100) таким образом, что среднеквадратичное отклонение равно (100)^? или 10¹ При этом сигнал, который мы должны обнаружить, составляет 1% яркости окружающего фона, тогда как шумовые флуктуации на площадках этих элементов картины достигают 10% средней яркости. (В нашем примере сигнал, подлежащий обнаружению, представляет собой разность между числом фотонов, падающих на исследуемую, площадку, и средним числом фотонов, падающих на равные по площади окружающие элементы.) Короче говоря, отношение сигнал/шум составляет 0,1, то есть значительно меньше 1, что часто принимается за порог различимости сигнала на флуктуирующем фоне.

Таким образом, чтобы флуктуации, или уровень шума, не превышали величину сигнала, который необходимо обнаружить, нам в первую очередь следует увеличить плотность падающих на холст фотонов. Поскольку наш сигнал представляет собой отклонение в 1% от окружающего фона, потребуем, чтобы уровень шума (или среднеквадратичное отклонение) также не превышал 1%. Этого можно добиться, если среднее число фотонов, падающих на каждый элемент картины, составит 10⁴. Среднеквадратичное отклонение тогда будет равно квадратному корню из 10⁴, то есть 10², а его отношение к среднему значению—10^-2, или 1%.

Резюмируя сказанное, мы должны отметить, что при переходе от черного пятна к серому, контраст которого по отношению к фону составляет 1%, число фотонов, требуемое для изображения одного пятна, возросло в 100 раз; это число увеличилось еще в 100 раз при учете случайного характера распределения фотонов. Последнее гарантирует, что сигнал, который необходимо обнаружить, равен среднеквадратичному отклонению, обусловленному совершенно случайным характером распределения фотонов.

Однако следует учесть еще один фактор, который поможет нам избежать ложных сигналов, то есть обеспечит возможность отличить реальный сигнал, подлежащий детектированию, от любой случайной флуктуации определенной величины.

Ложные сигналы. При расчете и анализе электронных систем часто считают, что порог различимости сигнала, соответствует равенству сигнала и шума. Это не совсем верно. Предположим, что мы измеряем величину электрического тока с целью обнаружить его колебания в 1 % или выше. Допустим также, что уровень шума (среднеквадратичное отклонение) составляет 1% среднего значения тока. Если мы выполним N последовательных измерений, то окажется, что ток будет отличаться от своего среднего значения на 1 % или более почти в половине случаев даже в отсутствие любого «реального», сознательно вызванного изменения тока. Мы заключаем слово «реальный» в кавычки, поскольку флуктуации, связанные с шумом, совершенно так же «реальны», как и сознательно вызываемые возмущения, — только источники возмущения в этих случаях различны. Итак, почти в половине наших измерений ток отклоняется от своего среднего значения на величину более 1% независимо от того, создаем ли мы сознательно какое-либо возмущение или нет. Именно в этом смысле мы говорим, что в половине случаев мы имеем дело с ложными сигналами. Чтобы можно было обнаружить «реальный» сигнал на фоне ложных сигналов, он должен превышать уровень шума в несколько раз. Превышение легко оценить, зная статистическое распределение шумовых флуктуаций, а также число наблюдений, при которых можно считать, что мы статистически свободны от ложных сигналов.

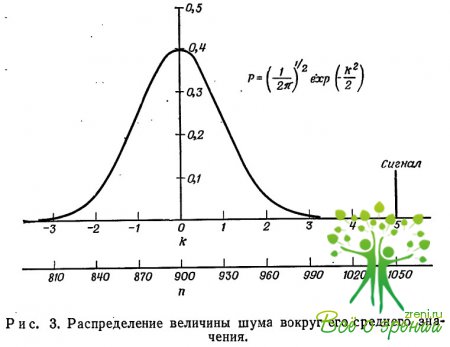
На рис. 3 показано распределение шумовых флуктуаций относительно среднего значения измеряемого параметра.

По оси ординат отложена плотность вероятности, а по оси абсцисс k — среднеквадратичное отклонение. Вторая шкала по оси" абсцисс относится к конкретному примеру, для которого среднее число фотонов составляет 900. В этом случае среднеквадратичное отклонение равно 30. Полная площадь, ограниченная кривой (при использовании абсциссы k), равна 1. Часть площади, заключенная, например, в интервале значений k = 1 —2, равна 0,13 и представляет собой вероятность того, что измеренная величина на 1 —2 единицы среднеквадратичного отклонения выше среднего значения. В нашем числовом примере это означает, что измеренное число фотонов лежит в пределах 930—960. Площадь, ограниченная частью кривой справа от
k = 2, равна 0,023 и представляет гобой вероятность того, что результат измерения превышает среднее значение на 2 единицы среднеквадратичного отклонения. В нашем числовом примере это вероятность того, что измеренное число фотонов превышает 960.

В табл. 1 приведена вероятность появления шумовых флуктуаций, которые превышают среднее значение фона на 1, 2, 3 и т. д. единиц среднеквадратичного отклонения. Для определения вероятности шумовых флуктуаций, значения которых лежат по обе стороны от среднего значения, величину вероятности, приведенную в таблице, необходимо удвоить.

С помощью табл. 1 можно определить, какой величины должен быть сигнал, чтобы мы могли избежать ложных сигналов.

В нашем случае сигнал равен разности средних значений яркости исследуемой площадки и фона. Предположим, что картина содержит 10⁵ элементов, каждый площадью, равной тестовой площадке. Тогда мы имеем 10⁵ возможностей возникновения ложного сигнала. Если мы стремимся снизить число ложных сигналов до величины, меньшей 1, то, согласно табл. 1, нам потребуется сигнал, амплитуда которого в 4—5 раз превышает среднеквадратичное отклонение. Назовем эту величину k пороговым отношением сигнал/шум. При величине сигнала, равной этому пороговому значению, мы можем быть достаточно уверены в том, что не примем за реальный сигнал флуктуацию шума. Отметим, что при k = 6 вероятность регистрации ложного сигнала уже значительно меньше, чем необходимо. С другой стороны, при k =. 3 мы «защищены» от ложных сигналов лишь в том случае, когда изображение содержит менее 103 элементов. Следовательно, k = 5 является разумным приближенным значением порогового отношения сигнал/шум.

Мы выбрали k равным 5, а не 4 по следующей причине. В вышеприведенном рассуждении мы предполагали, что имеем дело с точно определенным сигналом и фоном, характеризуемым большим шумом. Однако сам сигнал имеет почти такое же распределение, что и шум. Это означает, например, что если на рис. 3 средняя величина сигнала соответствует k = 4, то оказывается, что половину
времени сигнал приходится на область k 4. Если же принять, что сигнал соответствует k = 5, то в области значений k < 4 он будет находиться в течение только 0,15 полного времени наблюдения, то есть 85% времени мы будем воспринимать его как реальный сигнал.

Следовательно, запас примерно в одну единицу k по сравнению с номинальным значением, необходимый для того, чтобы избежать ложных сигналов, достаточен для обеспечения разумной надежности наших наблюдений.

Теперь вычислим, насколько должна увеличиться плотность фотонов (для выполнения критерия k = 5) по сравнению со случаем, рассмотренным в предыдущем разделе и соответствующим k=1. Начнем с условия k= 1, когда сигнал равен среднеквадратичному ^отклонению, или шуму. Положим для определенности, что сигнал и среднеквадратичное отклонение составляют 1 % яркости фона каждый. При увеличении плотности фотонов сигнал, измеряемый в процентах от яркости фона, остается постоянным. Однако среднеквадратичное отклонение шума уменьшается. Поскольку отношение последнего к средней яркости фона меняется как n₀^?/n₀=1/n₀^? где n₀ — средняя плотность фотонов, характеризующая фон, то для уменьшения отношения 1/n₀^? в k(=5) раз n₀ требуется увеличить в k² то есть в 25 раз.

Таким образом, требуемая плотность фотонов меняется пропорционально k² и для случая k = 5 плотность фотонов должна увеличиться в 25 раз по сравнению с плотностью, вычисленной в предыдущем разделе для k = 1. Там количество фотонов составляло 10⁴N, где N — число элементов в тестовом изображении. Следовательно, для защиты от ложных сигналов число фотонов следует увеличить до 2,5*10⁵N.

Теперь запишем общее выражение для полного числа фотонов, которое необходимо, чтобы мы могли обнаружить контраст С, где С есть сигнал, определяемый как доля от яркости фона, то есть С??B/D и 0?С?1 (С= 1 означает 100%-ный контраст, а С = 0,01 — контраст в 1%).

Полное число фотонов N*(1/C²)*k²                                                    (1.1)

где N — полное число элементов в тестовом изображении. Наличие этого множителя обусловлено дискретностью световых квантов. Множитель 1/C² связан с контрастом и отражает как случайный характер распределения фотонов, так и требование защиты от ложных сигналов.

↑ Итоговый эксперимент

Теперь обратимся к рис. 4, который поясняет выводы, сделанные в предыдущих разделах.

Здесь показана некая область, равномерно освещенная потоком фотонов низкой плотности. С помощью фотоумножителя с большим усилением каждый фотон отображается на телевизионном экране в виде дискретной белой точки. На рис. 4, а мы можем наблюдать дискретный характер фотонов, их хаотичное распределение, а следовательно, и «шум», то есть флуктуации, приводящие к появлению ложных сигналов. Разглядывая рис. 4, а, мы обнаруживаем черные площадки, или пятна, которые за неимением другой информации мы можем легко принять за «реальные» черные пятна. На самом деле такая картина черных пятен сознательно не создавалась: эти пятна являются следствием статистического характера распределения фотонов.

Рис. 4,б представляет собой «реальное» тестовое изображение черных пятен которые мы хотим различить в условиях низкой освещенности, соответствующих рис. 4, а. Для этого мы просто перемножим прозрачности рис. 4, а и 4, б и получим таким образом рис. 4, е. На рис. 4, в легко заметить четыре больших черных пятна, показанных на рис. 4, б. Остальные черные пятна меньшего размера на рис. 4, в неразличимы. Они теряются в шуме.

Создается также впечатление, что четыре пятна большего размера образуют фигуру, включающую пятое черное пятно, как вершину треугольника. Однако это пятое черное пятно представляет собой одно из самых больших черных пятен, обусловленных статистическим характером распределения фотонов и уже присутствующих на картине «однородной» освещенности, показанной на рис. 4,а. Для удобства это черное пятно указано на рис. 4, а и 4, в небольшими стрелками.

Присутствие на рис. 4,а ив пятна, обусловленного статистическим распределением фотонов, означает, что любое «реальное» черное пятно должно иметь большие размеры, чтобы мы могли с уверенностью утверждать, что оно «реально». Беря черное пятно, связанное со статистическим распределением фотонов, в качестве отправной точки находим,- что оно занимает примерно 1/500 часть площади картины. Всего на картине примерно 4500 точек,- следовательно, среднее число точек, приходящееся на площадь этого пятна, равно 9. Тогда отношение сигнал/шум составит ?9 = 3. Из табл. 1 находим, что при отношении сигнал/шум, равном 3, ложные сигналы наблюдаются в 1/1000 случаев от общего числа измерений. Поскольку имеется 500 элементов картины размером с интересующее нас черное пятно и поскольку вероятность образования такого пятна за счет статистических флуктуаций равна одной тысячной, то мы находимся на пороге надежной видимости «реальных» сигналов, то есть «реальных» черных пятен. «Реальные» черные пятна должны быть лишь несколько больше рассматриваемого нами пятна. В частности, если бы отношение сигнал/шум для «реального» пятна лежало в интервале от 3 до 4, мы могли бы с достаточной уверенностью говорить о его «реальности». Например, отношение сигнал/шум для наибольших пятен на рис. 4, в равно примерно 5, поскольку каждое из них включает примерно 25 белых точек. Эти большие черные пятна явно находятся выше порога надежной видимости, что подтверждает нашу оценку, согласно которой пороговое отношение сигнал/шум должно лежать в пределах 3—4.

Плотность фотонов, показанная на рис. 4, одна из самых низких, с которыми мы обычно имеем дело. Столь малую плотность мы выбрали сознательно для того, чтобы проиллюстрировать три основных свойства распределения фотонов: дискретность, хаотичность и наличие ложных сигналов. При больших плотностях фотонов, которые, как правило, встречаются на практике, число элементов картины составляет, по-видимому, величину порядка 10⁶, а не 10³, как это принято для рис. 4. В этих условиях пороговое отношение сигнал/шум необходимо увеличить до 4—5, чтобы предотвратить появление ложных сигналов. Согласно табл. 1, при k[/b] = 5 вероятность ложных сигналов равна всего лишь [b]3*10^-7. При k=6
она резко уменьшается до 2*10^-9. В качестве примера укажем, что изображение на экране телевизора включает примерно. 105 элементов, следовательно, k должно равняться 4—5.

Рис. 4, а служит еще одной цели. Он подчеркивает, сколь нереалистично было бы пользоваться обычным критерием видимости, а именно отношением сигнал/шум, равным 1. На практике этот критерий означает, что если один человек убирает одну из точек, показанных на рис. 4, а, то другой в состоянии определить, какая именно точка убрана. Удаление одной точки эквивалентно тому, что мы имеем тестовую картину, которая закрывает в среднем одну точку, или фотон. Тогда средний сигнал соответствует одному фотону; шум, который представляет собой корень квадратный из среднего сигнала, также соответствует одному фотону, что дает отношение сигнал/шум, равное 1. Простое рассмотрение рис. 4 показывает, что установить отсутствие одного фотона совершенно невозможно.

↑ Второй эксперимент

Все наши рассуждения касались различимости черных пятен, контраст для которых по определению равен 1. Для серых пятен С< 1, и, чтобы их можно было различить, они должны иметь большие размеры. Согласно соотношению (1.1),

Полное число фотонов = N*(1/C²)*k²=(A/(d²*C²))*k²                                                     (1.2)

где d — линейный размер элемента картины, или тестового пятна, А — площадь картины. Как видно из соотношения (1.2), при фиксированном полном числе фотонов (то есть при постоянной яркости) диаметр d тестового пятна, которое едва различимо, обратно пропорционален его контрасту С.

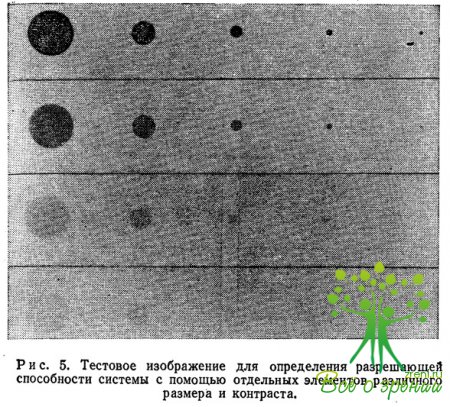
На рис. 5 представлена фотография тестового изображения, создаваемого дисками, диаметры которых при движении вправо вдоль строки убывают в геометрической прогрессии со знаменателем 2, а контрасты убывают по тому же закону при движении по столбцу сверху вниз.

Тогда произведение d*С остается постоянным вдоль диагоналей, образующих углы 45° с осями координат. Если осветить рис. 5 светом некой промежуточной интенсивности, то граница между различимой и неразличимой частями изображения должна проходить по одной из этих диагоналей.

На рис. 6 показано, как выглядит рис. 5 при освещении светом различной интенсивности.

Рис. 6 получен путем фотографирования изображения на экране кинескопа телевизионной системы. Тестовое изображение освещалось с помощью устройства, обеспечивающего развертку изображения движущимся световым пятном; при этом отраженный свет регистрировался фотоумножителем с большим усилением. Отметим, что рис. 6 был получен за несколько лет до рис. 4, и на первом заметны изменения интенсивности отдельных белых пятен, каждое из которых представляет собой сигнал от отдельного фотона. Эти изменения обусловлены зависимостью усиления фотоумножителя от расположения участка фотокатода, на который падает фотон. Для получения рис. 4 использовался ограничитель, с помощью которого интенсивность всех белых . точек была сделана примерно одинаковой.

На рис. .6 ясно видно, что граница между различимой и неразличимой частями рис. 5 проходит примерно вдоль диагонали под углом ,45°. к осям. При каждом увеличении интенсивности света в 4 раза эта граница смещается на один шаг вправо, в сторону дисков с диаметром, в 2 раза меньшим, как и следовало ожидать на основании соотношения (1.2). Серия картин, приведенная на рис. 6, использовалась ранее для оценки величины k, то есть порогового отношения сигнал/шум. Оказалось, что оно лежит в; пределах от 4 до 5.,Как мы уже говорили, при переходе от весьма малых плотностей фотонов (число элементов картины менее 10³) к большим плотностям (число элементов картины превышает 10⁵) это отношение должно быть увеличено с 3 до 5.

↑ Разрешающая способность, отношение сигнал/шум и тестовые изображения

Термин «элемент картины» мы использовали здесь для обозначения площади наименьшего разрешимого пятна с данным контрастом. Форма пятна не критична: оно может быть круглым, квадратным и даже прямоугольным. При определении отношения сигнал/шум по среднему числу фотонов наиболее существенна именно площадь пятна.

Как видно из рис. 6, элемент картины — понятие несколько растяжимое. Если мы рассматриваем маленькие черные пятна на белой поверхности, то число различимых элементов картины оказывается больше, чем в случае серых пятен, контраст которых мал по сравнению с белым фоном. Из рис. 6 и соотношения (1.2) следует, что число различимых элементов картины пропорционально квадрату их контраста. Число элементов картины, обладающих контрастом 1 (черные пятна), оказывается в 10⁴ раз больше, чем число элементов с контрастом 0,01, или 1%. Пренебрежение этим обстоятельством в течение многих лет служило причиной преувеличенных оценок разрешающей способности фотографической пленки.

Разрешающая способность пленки оценивалась по наименьшему расстоянию между черными и белыми полосами, которые можно было разрешить. Часто оказывалось, что при пользовании пленкой, которая, как утверждалось, позволяет разрешить, например* 2000 линий, не удавалось различить даже детали, раз* меры которых соответствуют разрешению в 400 линий. Такое несоответствие объяснялось, во-первых, тем, что интересующая нас деталь обладала меньшим контрастом, чем контраст черного и белого, и, во-вторых, эта деталь имела вид элемента картины, а не набора полос. Использование полос (а не отдельных пятен, показанных на рис. 5) приводит к существенной переоценке разрешающей способности системы: она кажется большей, поскольку при оценке отношения сигнал/шум обычно основываются на полной площади полос, а не на одной элементарной площадке, диаметр которой равен ширине одной полосы. Возвращаясь к рис. 4, отметим, что наименьшие черные пятна тестовой картины не видны на рис. 4, е. В то же время на нем легко различить длинную полосу, ширина которой немного меньше диаметра одного из самых малых черных пятен.

На раннем этапе развития телевидения для передачи кинофильмов использовались телевизионные каналы шириной порядка 100 МГц. При этом исходили из величины разрешающей способности пленки (2000 линий), которую тогда определяли с помощью картины из черных и белых полос. Между тем беглый просмотр текущих телевизионных программ показывает, что при передаче изображения с той же пленки (с разрешением 2000 линий) через современные телевизионные системы с разрешением 500 строк (ширина канала 5 МГц) качество изображения часто оказывается хуже, чем при передаче «живых» сцен непосредственно из студии. Это означает, что при разрешении 500 линий отношение сигнал/шум для этой пленки часто оказывается ниже, чем для телевизионной камеры, с помощью которой ведется передача непосредственно из студии.

На рис. 7 видно, к каким ошибкам при определении разрешения системы приводит использование в качестве тестовой картины набора полос.

Здесь представлена полученная Колтмэном серия изображений из десяти пар черных и белых полос/Число, стоящее под каждым изображением, указывает относительную освещенность тестовой картины. В данном случае освещенность была достаточно мала (а усиление системы достаточно велико), так что каждая белая точка обозначает фотон. Как видно из рисунка, даже на первом изображении, которое соответствует минимальной освещенности, можно обнаружить присутствие полос, например, если рассматривать изображение несколько под углом и вдоль его границ, сначала сбоку, а затем снизу. На этом изображении плотность фотонов чрезвычайно низка, и если бы мы взяли за элемент картины квадрат, сторона которого равна ширине полосы, то среднее число фотонов, приходящееся на этот элемент, было бы заметно меньше единицы, а точнее, близко к ?. Тогда отношение сигнал/шум для такого элемента составляло бы (?)^? или 0,5. Подобное использование термина «сигнал/шум» ошибочно, поскольку оно применяется здесь к элементу, размеры которого малы по сравнению с размерами той части картины, которую глаз видит на самом деле и которая используется при рассмотрении системы полос. Чтобы отношение сигнал/шум существенно превышало 1, глаз должен охватить значительную часть картины. Отдельные элементы, размер которых равен ширине полосы, конечно, совершенно неразличимы на первом и даже на втором изображении этой серии.

Рассмотрим также первый из серии снимков, приведенных на рис. 6. Он получен с экрана кинескопа телевизионной системы с разрешением 500 строк. Если бы мы оценивали отношение сигнал/шум для элемента, диаметр которого равен ширине линии на экране телевизора, основываясь на плотности фотонов, то мы получили бы величину, много меньшую 1. Поскольку число фотонов во всей картине составляет примерно несколько тысяч, а число элементов телевизионного изображения — несколько сотен тысяч, то на элемент изображения в среднем приходится 10^-2 фотона, а отношение сигнал/шум для этих элементов составляет 10^-1. Из рис. 6 отчетливо видно, что элементы столь малого размера и с таким низким отношением сигнал/шум лежат далеко за пределами видимости. Порога видимости и порогового отношения сигнал/шум,, равного примерно 4, мы достигаем лишь при переходе к самому большому черному пятну.
Таким образом, отношение сигнал/шум для объекта, который можно различить глазом, должно значительно превышать 1. Отношения сигнал/шум, меньшие 1, которые приводятся Колтмэном и Морганом, относятся к картине полос; в известной степени их можно использовать для сравнения, однако они не дают отношения сигнал/шум для участка изображения, которое на самом деле воспринимается глазом.

Отметим кстати, что смысл отношения сигнал/шум, когда оно меньше 1, неоднозначен. Например, приведенное выше отношение сигнал/шум, равное 0,1, соответствовало средней плотности 0,01 фотона на элемент картины. Следовательно, в среднем в 99 случаях из ста наблюдатель не обнаружит в элементе картины ни одного фотона, а одно-единственное наблюдение, строго говоря, вообще не может дать никакой информации о величине отношения сигнал/шум.

В практике кино и телевидения весьма распространена и другая ошибка: отношение сигнал/шум для элемента картины в одном кадре связывают с пороговой видимостью изображения, даваемого движущейся пленкой. Если бы время накопления сигнала глазом равнялось продолжительности демонстрации одного кадра в кино, такая связь была бы правильной. На самом деле время накопления для глаза составляет примерно 0,2 с, а демонстрация одного кадра (в телевизионной системе) происходит в течение 0,03 с. Следовательно, глаз по существу воспринимает суперпозицию примерно семи следующих друг за другом кадров; при этом отношение сигнал/шум по сравнению с таковым для отдельного кадра увеличивается примерно в 7^? раз. На отдельном кадре мы замечаем больше флуктуаций, чем мы можем зрительно наблюдать при обычной проекции движущейся пленки.

↑ Абсолютная шкала качества

Используя соотношение (1.2), мы можем построить абсолютную шкалу качества, которая позволит нам измерить качество любой реальной системы отображения. Величину порогового отношения сигнал/шум k примем равной 5, имея в виду, что при малых освещенностях она должна быть несколько ниже. К сожалению, до сих пор никому не удалось осуществить надежных измерений зависимости k от уровня освещенности. Запишем соотношение (1.2) для изображения площадью в 1 см² :

Число фотонов на 1 см² (фотон/см²)=n=25/(d²*C²)

Число разрешаемых линии на 1см=1/d=(C*n^?)/5                                                     (1.3)

Термин «число разрешаемых линий на 1 см» определяет здесь диаметр d наименьшего разрешимого изолированного пятна, обладающего контрастом С.

Этот термин не относится к обычно применяемому способу определения разрешающей способности с помощью системы полос равной ширины d. Последние, как мы уже говорили, в принципе лучше различимы, чем отдельные изолированные пятна.
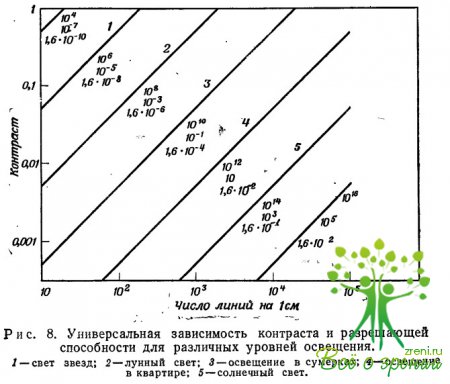
На рис. 8 представлены зависимости числа разрешаемых линий на 1 см от С, в качестве параметра взята плотность фотонов n.

Если мы знаем, например, что экспозиция поверхности изображения некой зрительной системы составляет 10¹⁰ фотон/см2[/sup], то тогда, согласно рис. 8, мы в состоянии различить черные и белые элементы (С= 1) с диаметром не менее 0,5*10^-4[sup] см. В то же время при контрасте 0,01 мы сможем различать толь-ко элементы, диаметр которых превышает 0,5*10[sup]-2 см. Все. это было бы справедливо, если бы зрительная?система в самом деле регистрировала каждый падающий фотон. Тогда ее квантовый выход был. бы равен 1 (что соответствует квантовой эффективности 100%).

Предположим теперь, что в действительности наименьший размер черно-белых элементов, которые может разрешить зрительная система при освещении ее поверхности потоком фотонов интенсивностью 10¹⁰ фотон/см², составляет лишь 0,5*10^-2 см вместо 0,5*10^-4 см. Тогда, согласно рис. 8, качество системы характеризуется квантовым выходом 0,01 или квантовой эффективностью 1%.

Параметры кривых на рис. 8 выражены в фотон/см2 и приведены для плоскости изображения. Для удобства эти единицы преобразованы также в единицы освещенности плоскости изображения, измеряемой в люксах (лк) при условии, что время экспозиции составляет 0.1 c ; переводной коэффициент равен 10¹⁶ фотон/с на 1 люмен (лм) белого света. Третий эквивалентный параметр, приведенный на рис. 8, представляет собой соответствующую яркость объекта в единицах ламберт (ламб) при условии, что используются линзы с относительным отверстием 1:2, а время экспозиции составляет 0,1 с. Наконец, указано соответствие различных уровней освещенности естественным условиям освещенности, начиная от света звездного неба до яркого солнечного света.

На рис. 8 отражены свойства идеальной зрительной системы, ограниченной шумами. Разрешающую способность реальных систем для маленьких черных тестовых элементов, по-видимому, ограничивают аберрации линз, дифракция или структура плоскости изображения. Аналогично способность реальных зрительных систем к передаче слабых контрастов на больших площадях может быть ограничена различными источниками шума, например неоднородностями регистрирующей среды. В результате кривая для реальной системы проходит не под углом 45°, а изгибается таким образом, что на ее краях, соответствующих высокому разрешению и низкому контрасту, качество системы оказывается хуже, чем в некоторой промежуточной части кривой. Именно такая зависимость характерна для рис, 6. К этому вопросу мы вернемся при анализе характеристик человеческого зрения»

↑ Ограничения качества изображения, обусловленные геометрическими факторами и шумами

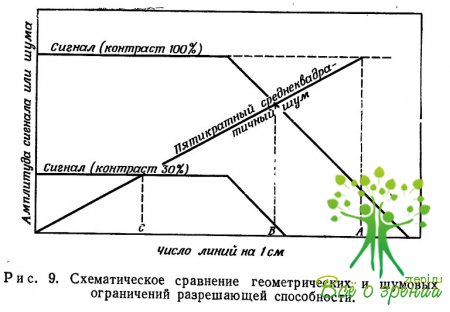
Все проведенные нами выкладки схематически представлены на рис. 9.

Сплошные кривые, обозначенные термином «сигнал», показывают зависимость амплитуды сигнала, даваемого системой отображения,? от числа линий на 1 см в тестовой картине. Ход этих кривых определяется геометрией системы и связанными с ней дифракцией, аберрациями линз и конечными размерами элементов отображающей поверхности. Кривая «пятикратный среднеквадратичный шум» показывает изменение шумового тока, который мы могли бы наблюдать при сканировании изображения с помощью серии оптических систем с различной апертурой, каждая из которых обладает определенной разрешающей способностью, выражаемой в числе линий на 1 см. (Чем меньше апертура, тем больше шумовой ток, который возрастает пропорционально числу линий на 1 см и обратно пропорционально ширине апертуры. Причина этого заключается в следующем: хотя среднеквадратичные флуктуации в пределах апертуры уменьшаются с ее размерами, линейная скорость, с которой эта апертура сканирует изображение, возрастает обратно пропорционально ее площади, то есть как квадрат обратной величины ее размера, если изображение сканируется в течение фиксированного времени. В результате совместного действия этих двух эффектов шумовой ток возрастает обратно пропорционально ширине апертуры. По тем же причинам ток сигнала не зависит от размеров апертуры.) Кривая шума, отмеченная на графике как «пятикратный среднеквадратичный шум», при пересечении с кривой «сигнал» непосредственно дает величину наименьшего разрешаемого элемента.

В отсутствие рассмотренных геометрических ограничений размеры наименьших разрешаемых элементов системы определялись бы положением точки А. В действительности влияние геометрических факторов приводит к тому, что эта граница находится в точке В и соответствует меньшему числу разрешаемых линий. Это справедливо для элементов картины, обладающих контрастом 100%, то есть контрастом черного и белого. Если мы обратимся к элементам с низким контрастом [кривая «сигнал (контраст 30%)»], то окажется, что указанная граница находится в точке С, где геометрические ограничения еще не существенны. Это справедливо и для слабо освещенных объектов.

Следует подчеркнуть то обстоятельство, что даже когда геометрические ограничения разрешающей способности начинают играть роль, они действуют избирательно только на высококонтрастные участки картины. Видимость и отношение сигнал/шум для частей с низким контрастом, по-видимому, остаются неизменными, а большая часть информации, содержащейся в обычной картине, передается низкоконтрастными элементами.

В нашей книге мы будем обращать основное внимание на ограничения, обусловленные конечным числом фотонов, и лишь слегка касаться менее фундаментальных ограничений, связанных с геометрическими свойствами системы.

↑ За пределами видимого спектра

Все наши рассуждения касались прежде всего из¬лучения в видимой области спектра (0,4 — 0,7 мкм). Но поскольку при этом мы исходим прежде всего из числа фотонов, то сказанное столь же хорошо применимо и к системам, детектирующим ультрафиолетовое, рентгеновское и гамма-излучение. Так, Штурм и Морган исследовали передачу информации конечным числом рентгеновских квантов. В случае видимого света и излучения с большими энергиями кванта вышеприведенные рассуждения можно распространить почти до произвольно низких плотностей фотонов, поскольку равновесная плотность этих фотонов при больших температурах исчезающе мала.

Наше рассмотрение применимо и к инфракрасному излучению. Однако здесь возникают трудности, связанные со значительной равновесной плотностью фотонов при обычных температурах. В этом случае абсолютно отсутствует темный фон. Действительно, плотность фотонов с длиной волны около 10 мкм, по* падающих на исследуемую поверхность с окружающих предметов или эмитируемых с нее, сравнима с плотностью, соответствующей яркому солнечному свету, и составляет примерно 10¹⁸ фотон/см²*с. При 3 мкм плотность равновесных фотонов по порядку величины близка к плотности при комнатном освещении, то есть примерно составляет 10^-2 ламб, а- при 1 мкм эта плотность эквивалентна фоновой плотности видимого излучения примерно 10^-8 ламб и, следовательно, много ниже абсолютного зрительного порога.

Общее выражение для потока фотонов, эмитируемого черным телом при температуре T, имеет вид
??/?²*exp(-(h?)/(kT)) фотон/см² * с * стерадиан

где ??— интервал оптических частот вблизи длины волны ?.

Видимость объектов в инфракрасной области спектра сложным образом зависит от характеристик используемого искусственного освещения, потока их собственного свечения, их излучательных способностей и разности их температур. Здесь мы только отметим, что для объектов, видимых благодаря их собственному излучению и обладающих одинаковыми излучательными способностями, контраст определяется выражением

,

где ?T—разность температур между объектом и окружающей его средой. Разность температур в 1 °С создает контраст примерно в 10% при длинах волн около 1 мкм и примерно 1% при ? ~ 10 мкм.

Информация, которую несет конечная порция света, ограничена дискретностью световых квантов, хаотическим характером их распределения и наличием ложных сигналов.

Отношение сигнал/шум для тестового элемента изображения определяется как отношение среднего числа фотонов, приходящихся на элемент (или разности средних чисел, относящихся к элементу и окружению), к среднеквадратичному отклонению. При среднем числе фотонов п отношение сигнал/шум составляет n^?.

Пороговым называют такое отношение сигнал/шум, которое требуется для предотвращения ложных сигналов. Его величина обычно равна примерно 5, но в условиях чрезвычайно малых освещенностей, возможно, уменьшается до 3.

Характеристика идеальной системы, свойства которой определяются фотонным шумом, выражается соотношением



где n — число фотонов на 1 см², d — диаметр тестового элемента, С(=?B/B)—контраст тестового элемента по отношению к окружению и k(=5)—пороговое отношение сигнал/шум.

Понятие «сигнал/шум» для системы имеет смысл только в том случае, если указан размер тестового элемента.

Понятие «разрешающая способность системы» имеет смысл только в том случае, если указан контраст тестового элемента.

Геометрические ограничения разрешающей способности сильнее влияют на элементы с высоким контрастом, чем на низкоконтрастные.

Картина полос лучше различима, чем изолированное пятно, диаметр которого равен ширине полосы.


-----

Статья из книги: Зрение человека и электронное зрение А.Роуз 1977
.