Яркость и острота зрения

Содержание:
Описание
↑ Квантовые флуктуации света
В гл. 2 упоминалось о том, что острота зрения соответствует дифракционной формуле, т. е. зрение полностью использует возможности, предоставляемые ему волновой природой света. Однако известно, что острота зрения уменьшается с падением яркости наблюдаемой картины и становится значительно ниже предела, обусловленного дифракционной формулой, в которую яркость вообще не входит.
Чтобы найти зависимость остроты зрения или разрешающей способности любого зрительного устройства от яркости, нужно учесть корпускулярную природу света. Светотехника обычно оперирует такими понятиям», как постоянный световой поток, постоянная яркость, постоянная освещенность и т. д. Однако следует помнить, что о постоянстве любой фотометрической величины можно говорить только в среднем и всегда в известных границах.
Предположим, что монохроматическая энергетическая освещенность Е, которую мы считаем одинаковой на всей площади и постоянной во времени, создана на площади о с коэффициентом поглощения а. Энергия, поглощаемая на поверхности за время t, очевидно дается выражением
Разобьем время t на ряд равных промежутков t1, t2 ...ti
и будем измерять Qi за каждый промежуток. Как бы ни была постоянна с макроскопической точки зрения освещенность Е, при достаточно малых интервалах ti мы заметим, что Qi не равны между собой и освещенность, вычисленная по формуле
уже не постоянная величина.
Не получим мы постоянного значения Ei и в том случае, если разобьем площадь на множество равных малых площадок а; и найдем соответствующие этим площадкам значения Qi.
Измерив т значений энергии Qi за каждый из интервалов времени ti, мы сможем вычислить среднее значение энергии по формуле
Qi отличается от Q? в среднем на величину ?Q, которая определяется формулой
Величину ?Q можно назвать средней квадратичной флуктуацией. Как бы тщательно мы ни стремились отмерить одинаковые порции световой энергии Qi, они всегда будут отличаться друг от друга, хотя бы из-за наличия флуктуаций света.
С. И. Вавилов указывает, что флуктуации света вызываются отчасти причинами, известными уже из классической физики, отчасти квантовой природой света. Но во всех практически используемых источниках света основную роль играют только квантовые флуктуации, для которых
где h — постоянная Планка, v — частота света. Поскольку hv — энергия одного кванта, то
где n— число квантов, а
Подставив (115) и (116) в (114), получим
Чем больше порция световой энергии, тем больше ее средняя квадратичная флуктуация. Но все наши приборы работают с некоторой относительной погрешностью и измеряют величину c точностью, ограничиваемой этой относительной погрешностью. Поэтому для любого прибора, в том числе и для глаза, существенна не абсолютная величина ?n, а отношение ее к числу квантов n, т. е. относительная квантовая флуктуация ?n/n. Разделив обе части (117) на n, получаем
Относительная квантовая флуктуация уменьшается с увеличением общего числа фотонов n. Поэтому в обычных световых измерениях мы не улавливаем этих флуктуаций. Достаточно сказать, что в потоке 1 лм за секунду пролетает около 2-1016 квантов, следовательно, относительная квантовая флуктуация равна 1,4-10-8, т. е. немногим более стомиллионной. Никакой фотометр не может уловить столь малой величины. Но если n становится малым, квантовые флуктуации могут оказаться весьма заметными, причем совершенно не имеет значения, что определяет малую величину n: малая освещенность, малое поглощение, малая площадь или малая длительность [см. формулу (110)].
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
↑ Опыты С. И. Вавилова
В классических опытах С. И. Вавилова и его сотрудников малое число квантов n обуславливалось малым размером источника света (3 или 6'), небольшой его яркостью, краткостью световой вспышки (0,1 с) и введением поглощающих светофильтров. Наблюдения велись в полной темноте после длительной темновой адаптации. Экспериментально определялась вероятность увидеть вспышку в зависимости от среднего числа n фотонов в ней. Число n заранее неизвестно, но оно пропорционально яркости вспышки:
где g—постоянный коэффициент.
При среднем числе n, получаемом от отдельной вспышки, фактически поглощается z фотонов. Вероятность для каждого значения z определяется формулой Пуассона
Предполагается существование порогового числа фотонов n0. Если z ? n0, вспышка замечена, если z < n0, вспышка не видна. Следовательно, чтобы рассчитать вероятность увидеть вспышку W(z ? n0), достаточно просуммировать вероятности W(z) от n0 до бесконечности:
Обратим внимание на то, что W(z ? n0) при заданном параметре n0 есть функция только среднего числа квантов n. Вычислив при n0 = 1, 2, 3 и т. д. значения W(z ? n0), можно построить семейство этих кривых. По оси абсцисс при этом следует откладывать не n, a lgn. Это позволяет сравнивать вычисленные кривые с экспериментальными. В самом деле, логарифмируя формулу (119), получаем lgn = lgg+lgL. Значит, переход от аргумента n к аргументу L сводится к прибавлению постоянного слагаемого, т. е. к смещению кривой вдоль оси абсцисс без изменения ее формы. Подобрав для каждой экспериментальной кривой наиболее близкую к ней теоретическую кривую, удавалось определить параметр n0 для данного наблюдателя.
Характер найденных статистических зависимостей соответствует формуле Пуассона, что подтверждает предположение о квантовых флуктуациях в числе поглощаемых квантов. Пороговое число квантов n0 для разных наблюдателей колебалось в пределах от 8 до 50 (в отдельных случаях оно оказывалось близким к двум). В пределах ? от 500 до 600 нм по данным С. И. Вавилова и его сотрудников n0 не зависит от длины волны. Н. И. Пинегин несколько позже показал ту же независимость n0 от длины волны в гораздо более широком диапазоне — от 405 до 700 нм.
В этом как раз и заключается достоинство метода С. И. Вавилова: весь расчет идет на уровне активно поглощенных квантов. Для фотонов синего или красного света вероятность активного поглощения меньше, чем для фотонов зеленого. Но если уж фотон поглощен, его качество не имеет значения.
Хехт нашел, что n0 = 5; 6 или 7. Боуман и Ван дер Вельден утверждают, что n = 2 и даже строят на этой основе двуквантовую теорию зрительного процесса.
↑ Квантовые флуктуации и разрешающая способность зрительного прибора
Работами С. И. Вавилова и других авторов было несомненно доказано, что глаз в некоторых условиях способен чувствовать действие столь малого числа квантов, что становится вполне заметной роль квантовых флуктуаций. В 1943 г. акад. А. Л. Лебедев высказал мысль, что квантовые флуктуации должны сказываться и при довольно высоких уровнях яркости, ограничивая разрешающую способность зрительных приборов, в том числе, конечно, и глаза. Эта идея была нами разработана теоретически и экспериментально.
Как мы уже говорили, квантовые флуктуации заметны в тех случаях, когда порция света мала, т. е. мало среднее число действующих фотонов n. Но для этого совсем не должна быть мала освещенность. На фотопленке, например, зачастую необходимо получить изображение с большим числом деталей (а значит, элементы изображения малой площади) при малой выдержке. Следовательно, даже при значительной освещенности Е сомножители ? и t могут быть настолько малы, что малой окажется и порция световой энергии Q [см. формулу (110)], а следовательно, и n. Нужно помнить, что для различения некоторой детали изображения площадью о важен ее контраст с фоном К, определяемый формулой (72). Выделим рядом с объектом, площадь которого о, такой же по площади элемент фона и сравним две порции световой энергии Qs и Q, получаемые зрительным прибором от объекта и от фона. Учитывая, что освещенность на приемнике зрительного прибора пропорциональна яркости соответствующих частей поля зрения, мы можем на основе формулы (119) привести формулу (72) к такому виду:
где ns и n — средние значения числа квантов, которые поглощаются на изображении объекта и равного по площади элемента фона. Нужно подчеркнуть, что ns и n — средние числа за время ?, в течение которого прибор может собирать и накоплять воздействие фотонов (например, выдержка фотоаппарата, время инерции зрения и т. п.). Истинные числа квантов zs и z могут значительно отличаться от ns и n [см. формулу (120)]. Поэтому формула (122) дает только среднее значение контраста, а для получения некоторого истинного контраста К' вместо ns и n нужно подставлять zs и z.
Приведем такой пример. Пусть n = 1225, a ns = 784; при этом К = 0,36.
Для оценки К' возьмем неблагоприятный случай, когда флуктуации уменьшают п и увеличивают ns, уменьшая разницу между ними. Согласно формуле (117)
Контраст изменился незначительно.
Допустим, что вследствие падения освещенности n иns уменьшились в 49 раз. Теперь n = 25; ns = 16. Как и раньше К = 0,36. Но
Контраст К стал величиной колеблющейся, неустойчивой, временами доходящей до нуля. Улавливать его, т. е. обнаруживать контрастирующий объект, становится трудно, а быть может, уже и невозможно.
Мы видели, что неустойчивость контраста возрастаете уменьшением n. Очевидно, должно существовать такое минимальное пороговое значение n1, при котором едва улавливается объект даже со 100%-ным контрастом, К = 1.
Назовем ?1 угловой размер (в радианах) едва различаемого при К = 1 объекта, d — диаметр зрачка глаза (в метрах), L — яркость фона (в кд/м2), a1 — максимальный коэффициент активного поглощения, т. е. отношение поглощенного рецепторами сетчатки потока к потоку, вошедшему в глаз, для света, у которого V(?) максимально. Можно рассчитать, что
где М — коэффициент для перевода световой энергии в число фотонов. Расчет показывает, что для дневного (фотопического) зрения Мф = 16,8*1014 лм-1*с-1; для ночного или сумеречного зрения Мс = 7,0*1014 лм-1 - с-1.
Если бы n1 было известно, предельный угол ? в зависимости от яркости L можно было бы найти по формуле (123). Мы пошли сначала обратным путем и, воспользовавшись литературными данными для a1, d, ? и ?, приблизительно оценили значение числа n1. Оценка дала n1 ? 10. Интересно отметить, что при изменении яркости в 100 000 раз для сохранения постоянства n1 величина a1 должна изменяться только в 20 раз: от 0,2 при самой малой яркости (3-10~5 кд/м2) до 0,01 при яркости 3 кд/м2.
Для уточнения величины n1 были проведены модельные опыты. Тест-объект был выполнен в виде квадратика из черной бумаги размером в 7,3', наклеенного на матовое стекло. Матовое стекло освещалось проецированием на. него двух дисков со множеством беспорядочно расположенных отверстии. Диски вращались в противоположные стороны, при совпадении отверстий на матовом стекле происходила вспышка: на короткое время появлялось светлое пятнышко. Чем быстрее вращались диски, тем больше в единицу времени происходило вспышек на единице площади стекла и тем лучше становился виден квадратик. При этом яркость матового стекла, усредненная по поверхности и по времени, оставалась постоянной. Определяли ту скорость вращения дисков, при которой наблюдатель едва различал марку. Правильность его ответов контролировалась тем, что он должен был указать положение квадратика по отношению к центру круглого матового стекла: вверху, внизу, справа и слева. Наблюдения проводились при двух средних яркостях и двух длительностях наблюдения: 3 и 1,5 с. Время наблюдения почти не влияло на результаты, так как основное значение имеет число вспышек не за все время наблюдения, а за время инерции ?, в течение которого глаз усредняет воздействие вспышек. Результат экспериментального определения среднего числа вспышек, которые должны происходить на площади фона, равной площади квадратика, за время инерции ?, чтобы объект со стопроцентным контрастом (черный квадратик) различался на пороге видимости, был n1 = 5.
Роуз, создавая поле модельного наблюдения на экране электронного устройства, получил n1 = 25. Однако Роуз считал, что ? = 0,2 с, а это в 3—4 раза превосходит принятую нами величину 0,05—0,06 с, основанную на целом ряде специальных исследований. Если соответствующим образом пересчитать результаты Роуза, мы получим, что и у него n1 лежит в пределах от 6 до 8. А поскольку при вычислении ?1 по формуле (123) n1 входит в степени половина, можно, не рискуя ошибиться, принять ?n1 = 2,5.
Теперь следует перейти от n1— числа квантов, необходимого для различения объекта с контрастом К = 1, к n — числу квантов, необходимому для различения объекта с любым контрастом К. Если К ? 1, с площади изображения объекта на сетчатке за время ? поглощается ns квантов (при К = 1 ns = 0). Для различения объекта на равном ему по площади элементе фона, от которого глаз поглощает n квантов, необходимо, чтобы разность n — ns была достаточно велика. Она должна не менее, чем в некоторое число b раз, превышать среднюю вероятную флуктуацию, которая равна ?n. Таким образом, пороговое условие
(По существу, b—отношение сигнала к шуму.) Разделив обе части равенства (124) на n, получим
Поскольку при n = n1 К = 1, то 1 =b/?n1, откуда b = ?n1, а
При любом контрасте К для различения объекта с угловым размером ? требуется n квантов.
Формулу (123) следует переписать в виде
Подставив в (127) значение п по формуле (126), решим полученное уравнение для предельного угла
Следует заметить, что формула (128) универсальна. Она годится не только для глаза, а для любого зрительного устройства, т. е. для прибора, строящего изображение: для телескопа, фотоаппарата, электронно-оптического преобразователя. В зависимости от приемника света в приборе его спектральную чувствительность следует учитывать определенными значениями М и а1 время, в течение которого суммируются кванты (выдержка при фотосъемке, инерция фосфора), задается параметром ?. Вместо d следует, конечно, подставить D — диаметр входного зрачка. Обозначив
получим
Выражение (130) можно назвать флуктуационной формулой для предельного угла, разрешаемого любым зрительным прибором. Сравнив ее с дифракционной формулой (2), видим, что в обе формулы диаметр входного зрачка входит одинаково: согласно обеим предельный угол обратно пропорционален диаметру входного зрачка. Но во флуктуационной формуле появились яркость L и контраст К, от которых дифракционный угол разрешения не зависит. Практически вычислять ? для глаза по формулам (129) и (130) трудно, так как в них М, а1, ? и D (т. е. dr) зависят от яркости.
Для К = 1 мы вывели полуэмпирическую формулу, основываясь на следующих соображениях. Согласно формуле (130) предельный угол б должен уменьшаться пропорционально корню квадратному из яркости, иначе говоря, угол б пропорционален L-0,5. Однако в органе зрения с падением яркости происходит ряд компенсирующих процессов: усиление концентрации светочувствительных веществ, т. е. возрастание a1, расширение зрачка, увеличение времени инерции ?. Из формул (129) и (130) легко видеть, что при падении яркости все эти процессы замедляют рост ?. Формально такое замедление можно учесть, уменьшив степень яркости, т. е. поставив вместо 1/2 некоторую степень ?. Затем следует принять во внимание, что вследствие структуры сетчатки с ростом L предельный угол ? не может уменьшаться безгранично: он не может стать меньше размера структурного элемента сетчатки ?0.
Таким образом, теоретические соображения обусловили такой вид формулы:
Постоянные ?0, а и ? были найдены путем обработки экспериментальных данных Гершуна, Литго, Раутиана и Пинегина. В результате была получена формула, дающая предельный угол в минутах:
Рассмотрение вопроса на квантовом уровне позволило установить важную для практики зависимость между предельно разрешимым углом ?1 и яркостью фона L.
↑ Биологическая роль инерции зрения
Острота зрения V есть величина, обратная предельному углу ?. Из формулы (128) видно, что
Обратим внимание на то, что время инерции стоит в числителе. Инерционность зрения мешает наблюдению кратковременных или быстро развивающихся процессов. Но она совершенно необходима для того, чтобы мы вообще могли различать детали, т. е. не просто воспринимать свет, а видеть. В единичном зрительном акте должно быть использовано не слишком малое число фотонов, чтобы флуктуации их не обратили наблюдаемую картину в хаос. Повышение остроты зрения означает уменьшение площади ? различаемой детали (которая пропорциональна ?2), а это уменьшение можно компенсировать увеличением времени суммирования, т. е. ?. Для того чтобы обеспечить заданное число квантов n, должно соблюдаться (при неизменности остальных параметров) условие ?2? = С2, где С—константа, или V = ??/С. При повышении яркости, как известно, ? уменьшается, так как, чем больше яркость, тем легче собрать нужное число квантов на разрешаемом элементе. Но если бы ? стало близким к пулю, к нулю приблизилась бы и разрешающая способность глаза.
----
Статья из книги: Глаз и свет | Луизов А.В.





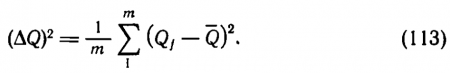







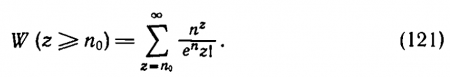

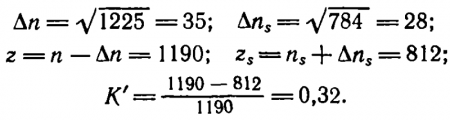
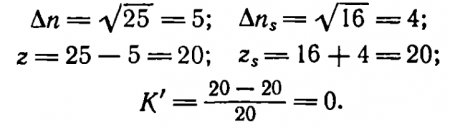











Комментариев 0