Пороговые условия

Содержание:
Описание
↑ Система зрительных функций
Зрение человека обычно характеризуют несколькими функциями, прежде всего тремя:
- световой чувствительностью,
- контрастной чувствительностью
- и остротой зрения.
где f и F—некоторые функции стоящих в скобках величин. Однако лучше, чтобы показать равноправность величин L, К и ? найти функцию, связывающую все эти величины, типа
Геометрически функция (135) может быть представлена как поверхность в трехмерном пространстве с осями L, К и ?. Если точка лежит ниже этой поверхности, объект невидим, а если выше — виден. Сама поверхность соответствует условиям пороговой видимости, определяет пороговые условия.
Если объект появляется на короткое время т, оно тоже должно учитываться при определении пороговых условий, которые станут уже поверхностью в четырехмерном пространстве. При более строгом подходе следует ввести еще вероятность увидеть объект, что сделает пространство уже пятимерным. Но во всех случаях пороговые условия можно (по крайней мере, принципиально) выразить функцией типа (135) с тем или иным числом взаимосвязанных переменных.
Аналогичные пороговые условия определяют и видимость точечных источников света или проблесковых огней.
↑ Пороговая видимость протяженного объекта
Выведенная нами формула (132) дает связь между предельным углом и яркостью при контрасте, равном единице, т. е. связь между ?1 и L. Следует решить, как ввести в формулу контраст К, отличный от единицы, т. е. определить взаимосвязь типа (134).
Н. Г. Болдырев построил теорию пороговых условий видимости, которую он назвал энергетической. Основное положение этой теории заключается в том, что для того, чтобы сигнал был воспринят, его энергия должна быть не меньше некоторого минимального (порогового) значения. Обработка с помощью энергетической теории некоторых экспериментальных данных показала хорошее согласие теории с экспериментом.
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
По энергетической теории в пороговых условиях соотношение между контрастом и размером объекта при постоянной яркости фона выражается формулой
где ? — пороговый контраст большого объекта, С, — некоторая постоянная энергетической теории при данной яркости фона.
Если К ? ?, можно написать приближенную формулу
которая аналогична закону Рикко для световой чувствительности, где на месте К стоит L — яркость источника света.
Квантовая теория, это явствует из сопоставления формул (126) — (130), дает аналог закона Пиппера
Однако формулы (136) и (137) обе основаны на чисто физических законах. В них не учтены особенности строения и работы глаза, прежде всего дискретная структура сетчатки и ограниченная способность суммирования световых воздействий по площади. Неполнота пространственного суммирования учтена Болдыревым величиной ?, которая вычитается из К, что и приближает расчеты к экспериментальным результатам.
Если же ограничиваться только выбором показателя степени при ?, приходится констатировать, что ни первая, ни вторая степень не может удовлетворять экспериментальным данным в широкой области изменения предельных углов, контрастов и яркостей фона. Более соответствующий эксперименту показатель степени лежит где-то между единицей и двумя.
Вейнберг на основе обработки своих экспериментов и литературных данных предложил формулу, которую можно представить в виде
Сам Вейнберг указывает, что при малых яркостях наблюдаются отклонения от его формулы. Кроме того, она явно непригодна, когда К становится меньше порогового контраста в, тогда объект не виден даже при очень большом его размере. До некоторой степени этот недостаток формулы (138) можно уменьшить способом, аналогичным тому, которым воспользовался Н. Г. Болдырев [см. формулу (136)]. Конечно, ? — величина, зависящая от яркости. Однако зависимость от яркости в основном учтена значением угла ?1 [см. формулу (132)]. Поэтому для приближенных вычислений вместо ? можно взять постоянное число 0,02, близкое к значению порогового контраста при высоких яркостях. Таким образом приходим к формуле предельного угла (в минутах)
Коэффициенты в числителе несколько отличаются от коэффициентов формулы (132), так как при К = 1 должно выполняться условие ? = ?1. Формула (140) не может претендовать на большую точность, но для ориентировочных расчетов она пригодна, пока К > ?.
↑ Фактор времени
Формула (140) может быть использована только в случаях, когда время наблюдения неограниченно. Если же время наблюдения т невелико, оно начинает влиять на пороговые условия и должно быть введено в соответствующую формулу. Очевидно, т перестает влиять на величину ? в тех случаях, когда т ? ?. Расчет по формуле (82) показывает, что уже при т = 4? эффективный контраст Кэ только на 2% меньше контраста К. Значит, если время наблюдения больше секунды, формулой (140) можно пользоваться без всяких поправок. Если же т составляет доли секунды, учет времени экспозиции необходим.
Время наблюдения т может влиять на восприятие и яркости L, и контраста К. Рассмотрим два предельных случая: в первом изменяется только эффективная яркость, во втором — только эффективный контраст. Если глаза наблюдателя все время погружены в темноту (все время «видят» темноту), а потом на время т появляются и фон и объект, в формулу (140) вместо яркости L следует ставить эффективную яркость Lэ, которую можно рассчитать по формуле
Значение ? нужно брать для самой малой яркости (темнота), к которой адаптировался наблюдатель до появления объекта и фона. Если т ? ?, можно воспользоваться упрощенной формулой, аналогичной формуле (76):
но, как показал опыт, в формулу (140) следует поставить не Lэ, а только 0,2 Lэ. Эмпирически найденный коэффициент 0,2 характеризует ухудшение остроты зрения, объясняемое тем, что за очень короткое время т глазу трудно «разобраться» в наблюдаемой картине.
Иначе обстоит дело, когда наблюдатель непрерывно видит фон яркостью L, а объект с контрастом К появляется на короткое время т. Теперь Lэ — L, т. е. L в формуле (140) остается неизменным, а вместо контраста К нужно поставить эффективный контраст Кэ, вычисленный по формуле (82) или, если т ? ?, по формуле (76).
↑ Видимость точечного источника
При переходе к точечным источникам света пороговые условия упрощаются, так как число входных данных уменьшается: вместо углового размера объекта ? и его контраста с фоном К появляется одна характеристика — блеск источника Е. Таким образом, даже для проблесковых огней, когда необходимо учитывать длительность проблеска т, пороговые условия определяются только тремя величинами: блеском огня Е, его длительностью т и яркостью фона L. В гл. 9 было показано, что связь между Е и т на пороге видимости определяется формулой Блонделя и Рея. Однако лучше получить эти параметры по аналитическим формулам Для времени инерции ? уже была приведена формула (99) Зависимость порогового блеска от яркости фона выведена в работе Травниково. Для фовеального зрения от самых малых яркостей до яркости L = 10-3 кд/м2 пороговый блеск постоянен и равен 2• 10-8 лк. При L ? 10-3 кд/м2 действует формула
где
Заметим, что при яркости фона 3•10-3 кд/м2 вся сетчатка одинаково чувствительна к блеску точечного источника. При меньших яркостях чувствительнее периферия, при больших — фовеа.
↑ Зрительный поиск
Во всех экспериментах по определению пороговых условий наблюдатель знал заранеe, где находится или может появиться тест-объект. Но на практике так бывает довольно редко. Зона, в которой может находиться интересующий наблюдателя предмет, как правило, достаточно велика. Обнаружение его, таким образом, связано с поиском. А при поиске вероятность обнаружить объект растет с увеличением времени поиска t. Здесь мы снова вводим фактор времени t, но смысл его уже не тот, что в § 75. Теперь объект находится в поле зрения непрерывно в течение долгого (теоретически бесконечно долгого) времени, а t — длительность времени, затраченного на поиск. Поиск есть процесс вероятностный, и теория дает для вероятности найти объект за время t формулу
где tср — среднее время, которое нужно затратить, чтобы найти объект в данных условиях. А условия эти для поиска одиночного объекта на однородном фоне определяются в основном четырьмя параметрами: размером объекта ?, его контрастом с фоном К, яркостью фона L и угловым размером поля зрения 2?. Мы предполагаем, что поле поиска имеет форму круга и 2? — угловой диаметр этого круга. Объект виден в форме квадрата и ? — угловой размер его стороны.
Две величины характеризуют процесс поиска: время поиска t и вероятность обнаружить объект за это время W. Таким образом, формула, определяющая закономерность поиска, должна связать шесть величин: L, К, ?, 2?, t и W. Проведя обширные экспериментальные исследования, Травникова для поиска на однородном поле одинаковой во всех точках яркости подтвердила правильность формулы (145) и нашла, что
Коэффициент аb характеризует поисковую способность наблюдателя при бинокулярном зрении: чем больше аb, тем меньше (при прочих равных условиях) среднее время, затрачиваемое на отыскание объекта. Среднее значение этого коэффициента для бинокулярного наблюдения получено таким: аb = 16(...°)2 (...')-3 (кд/m2)-0,3*с-1. Усложнение размерности обусловлено тем, что 20 принято измерять в градусах, а ? — в минутах.
Введя в формулу (145) значение tср по формуле (146), мы получим формулу, связывающую все шесть параметров поиска, позволяющую найти любой из них, когда указаны остальные пять. Аналогичную формулу Травникова получила и для поиска точечного источника. При L ? 10_3 кд/м2
Значения у следует брать по формулам (144). Подставив значение tср в формулу (146), мы снова получаем связь между всеми параметрами поиска, но уже не между шестью, а только между пятью величинами, потому что, как уже было сказано, вместо контраста и углового размера точечный источник характеризует теперь лишь одна величина — блеск Е. Среднее значение коэффициента аb при бинокулярном наблюдении оказалось равным 2,6* 1014(...°)2(кд/м2)2? лк-2*-с-1.
Если поле зрения имеет не круглую, а какую-нибудь другую форму, за 2? можно принимать угловой диаметр равновеликого круга, что подтверждено экспериментально.
Формулы, определяющие закономерности поиска, можно рассматривать как обобщение пороговых условий, распространение их на случай, когда положение объекта заранее неизвестно. Поскольку вне лаборатории чаще всего именно так и бывает, практическое значение этих формул весьма велико. Пороговые условия определяют поверхность уже не в трехмерном, а в шестимерном (или пятимерном — для точечного источника) пространстве.
----
Статья из книги: Глаз и свет | Луизов А.В.


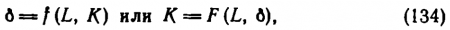





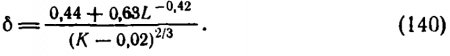



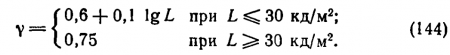



Комментариев 0