Твердотельные фотоумножители

Содержание:
Описание
↑ Введение
Создание вакуумного фотоумножителя, обладающего способностью детектировать отдельные фотоны, послужило мощным толчком к разработке различных датчиков. Однако вакуумный фотоумножитель пригоден лишь для передачи одного элемента картины. Тот же принцип умножения был использован в нескольких типах усилителей изображения большой площади. Эти усилители изображения постепенно все шире применяются в тех случаях, когда поток фотонов ограничен.
При всей результативности подобных вакуумных устройств их характеристики все же продолжают желать лучшего. Их квантовая эффективность порядка 10% (а не 100%), а размеры слишком велики. Для работы таких датчиков требуется напряжение до 10 кВт и выше. И наконец, очень трудно расширить их спектральную чувствительность в инфракрасную область, до длин волн порядка микрометра. Правда, здесь намечается некоторый прогресс, связанный с применением «гибридных» конструкций, в которых полупроводниковые фотоэмиттеры работают в вакууме.
Если мы по тем же параметрам оценим твердотельные фотоумножители, то формально их использование открывает значительные перспективы. Твердотельные датчики уже сейчас работают с квантовой эффективностью 100% не только в видимой, но и в инфракрасной (~10 мкм) области спектра. Твердотельный фотоумножитель должен иметь толщину порядка нескольких микрометров. Напряжения, которые необходимо прикладывать к слоям такой толщины, не превосходят нескольких сотен или тысяч вольт.
При успешной реализации твердотельного фотоумножителя он должен быть не только предельно чувствительным, но и предельно компактным и удобным.
По иронии судьбы процесс умножения в твердом теле представляет собой одно из наиболее давно изучаемых электронных явлений. Фрёлих и фон Хиппель еще в 30-е годы в своих ранних работах приводили серьезные аргументы в пользу того, что пробой в диэлектрике есть следствие лавинного умножения отдельных электронов, выходящих из катода и создающих вблизи анода множество свободных носителей. В упрощенном виде их рассуждения выглядели так. В поле напряженностью 106 В/см электрон может приобрести энергию в несколько электрон-вольт на длине в несколько сотен ангстрем.
Затем путем ударной ионизации он создает свободные электрон и дырку. Если бы этот процесс повторялся каждые несколько сотен ангстрем, то на отрезке в 1 мкм один электрон создал бы примерно 1010 свободных носителей. Через.2 мкм это число возросло бы до 1020 и оказалось бы вполне достаточным для того, чтобы вызвать пробой диэлектрика путем его теплового разрушения или разложения. Коль скоро ударная ионизация началась, она может привести к колоссальному умножению числа носителей на расстояниях всего лишь в несколько микрометров. Более того, если бы эта теория пробоя диэлектрика была правильной, то электронное умножение происходило бы в лаборатории ежедневно, стоило лишь инженеру случайно приложить к конденсатору избыточное напряжение и вызвать электрический пробой.
Единственным недостающим звеном между этими примитивными наблюдениями пробоя и в высшей степени сложным принципом действия датчика изображения являлось получение высоких и контролируемых величин коэффициента умножения. Для этого требовалось, например, приложить к тонкой изолирующей пленке фотопроводящего материала сильное электрическое поле таким образом, чтобы в темноте в пленке не возникало ни одного электрона, способного положить начало цепному процессу умножения. В подобных условиях попадание на катод даже малого количества фотонов привело бы к появлению также малого количества электронов и далее к возникновению на аноде легко измеримых импульсов тока. Тогда отдельные фотоны было бы легко обнаружить. Существующие системы для копирования документов, в которых используются тонкие изолирующие слои аморфного селена («Ксерокс») или порошок окиси цинка («Электрофакс»), должны служить идеальными объектами для подобного рода наблюдений. Эти материалы являются превосходными изоляторами, кроме того, метод нанесения заряда с помощью коронного разряда гарантирует возможность получения наиболее высоких значений поля (благодаря запирающему характеру ионного заряда). Однако до сих пор такого типа умножения обнаружить не удалось.
Отсутствие успеха в создании твердотельных фото-умножителей на основе изолирующих материалов обусловлено рядом причин фундаментального характера.
Во-первых, сильные электрические поля, необходимые для возникновения ударной ионизации, вызывают инжекцию электронов с катода путем туннелирования. Весьма вероятно, что пробой диэлектриков скорее обусловлен этими носителями, инжектируемыми под действием поля, нежели процессом лавинного умножения.
Во-вторых, процесс умножения в диэлектриках нелегко контролировать. Согласно данным эксперимента, пробой изоляторов происходит при строго определенном пороговом значении поля. Теоретически переход в режим ударной ионизации в полярных изоляторах должен выглядеть почти катастрофическим. В этом отношении диэлектрики резко отличаются от некоторых полупроводников с ковалентной связью атомов, таких, как германий и кремний, где степень умножения в определенных пределах можно контролировать.
Ниже мы рассмотрим физические основы столь пессимистической оценки возможности использования изолирующих материалов для создания твердотельных фотоумножителей. Перспективы реализации процесса умножения в полупроводниках выглядят более оптимистично. Об этом мы расскажем в следующем разделе, а затем проанализируем основные различия между изоляторами и, полупроводниками.
↑ Умножение в полупроводниках
Процесс электронного умножения в контролируемых условиях наблюдался в следующих полупроводниках: германии, кремнии, арсениде галлия, фосфиде галлия и антимониде индия. Однако даже в этих немногочисленных материалах надежные измерения оказались возможны лишь после того, как был освоен процесс выращивания кристаллов без дислокаций.
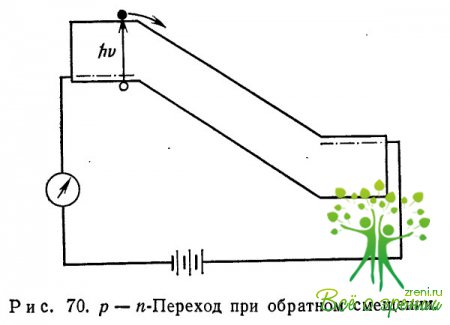
Обычно измерения выполняются на р — n-переходах, находящихся при обратном смещении (рис. 70).
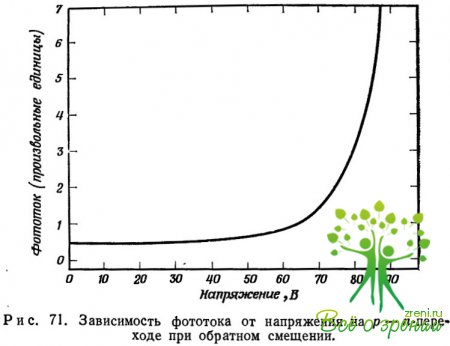
С помощью света индуцируются электроны у катодной части перехода или дырки — у анодной. При слабых полях ток через переход постоянен, он не зависит от величины поля и равен току фотовозбужденных носителей. При увеличении поля ток через переход возрастает благодаря ударной ионизации и последующего умножения числа носителей, проходящих через переход (рис. 71).
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
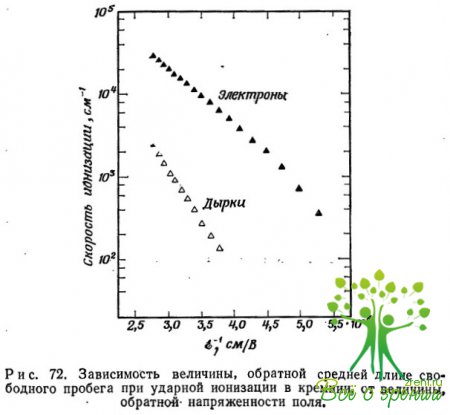
Каждому значению поля соответствует определенное значение параметра ? — величины, обратной среднему расстоянию, проходимому электроном или дыркой до образования пары свободных носителей. На рис. 72 показаны типичные кривые зависимости ? от электрического поля для электронов и дырок в кремнии.
Отметим два важных обстоятельства.
Во-первых, согласно рис. 72, существенное умножение наблюдается при напряженностях поля в интервале 105— 106 В/см. Это довольно сильные поля в том смысле, что при них становится значительным конкурирующий процесс полевой эмиссии, или туннелированныя. В материалах с более выраженными изолирующими свойствами, обладающих большей шириной запрещенной зоны, для заметного умножения требуются еще большие поля, поэтому роль процесса полевой эмиссии увеличивается.
Во-вторых, крутизна вольт-амперной характеристики возрастает при коэффициентах умножения свыше 5—10. Вследствие этого при коэффициентах умножения, превышающих 100, почти невозможно" достичь однородного умножения при сколько-нибудь значительной площади изображения. В этом случае требования, предъявляемые к однородности материала или электрического поля, становятся нереальными.
Крутизна вольт-амперной характеристики, а также шумы, возникающие в процессе умножения, зависят от соотношения между скоростями ионизации, производимой электронами и дырками. Предположим, что электроны и дырки обладают одинаковыми скоростями ионизации. Тогда исходный фотовозбужденный электрон при прохождении через переход создает электронно-дырочную пару с вероятностью ?. Мы считаем, что ? меньше 1, но близка к ней. Если пара возникает вблизи анода, то дырка с вероятностью ? может создать еще одну пару при прохождении через переход в направлении, катода. Полное число пар, образующихся в результате такого процесса, равно
Таким образом, коэффициент умножения G по мере его возрастания становится все более острой функцией ? (или напряжения на переходе). Величина G = 103 соответствует ? = 0,999, а это значит, что однородность процесса умножения должна быть не ниже 0,1%.
Данный тип умножения обладает еще одним недостатком. Он в принципе дает большие шумы, чем вакуумный фотоумножитель. Последний представляет собой усилитель, не вносящий шумов; отношение сигнал/шум на его выходе с точностью до множителя, равного 2, совпадает с таковым для попадающих на фотоумножитель фотоэлектронов. В твердом же теле сам по себе процесс умножения хаотичен, то есть создает шум. Среднеквадратичная флуктуация коэффициента умножения обусловливает шум, превышающий дробовой шум падающего потока света. Таким образом, если R есть отношение сигнал/шум для падающего светового потока (или электронного тока до умножения), то после умножения оно уменьшается до величины порядка R/G? где G — коэффициент умножения.
Однако умножение, достигаемое в р — n-переходе, находящемся при обратном смещении, оказывается полезным для некоторых приложений. Соответствующие системы в известном смысле можно противопоставить отображающим устройствам с высокой чувствительностью, работающим при малых освещенностях. Например, если нужно передавать сигнал (носитель информации) при больших интенсивностях света и с большой скоростью и если основной источник шума системы не связан с сигнальным пучком, то детектирование с использованием механизма умножения в р — n-переходе при обратном смещении обладает определенными преимуществами.
Теперь предположи, что умножение могут создавать только электроны, а свободные дырки преодолевают переход, не производя ударной ионизации. Этот процесс,. значительно лучше поддается контролю и вносит меньший шум, чем только что рассмотренный^ лавинный процесс. Если длина перехода равна L, а величина, обратная средней длине свободного пробега при ионизации, есть ?, то коэффициент умножения определяется соотношением

Хотя это выражение говорит о довольно резкой зависимости G от ?, она все же менее резка, чем зависимость, представленная соотношением (9.1). Если, на« пример, как в предыдущем случае, принять G = 103, то произведение L*? равно 7. Тогда изменение ? на 1% вызывает изменение G всего лишь на 7%. В рассмотренном выше примере изменение ? (или его эквивалента ?=L*?) на 1% приводило к «катастрофическому» изменению G.
Еще одно преимущество умножителя данного типа состоит в том, что по своим усилительным свойствам он приближается к вакуумному фотоумножителю, свободному от шумов. В рассматриваемом случае шум связан со статистическим характером ?, то есть показателя экспоненты L*?. Это означает, что число ступеней умножения меняется по статистическим законам. Анализ шумовых свойств этого типа умножения, проведенный в рамках некоторых вполне разумных предположений, показывает, что вносимый шум сравним с дробовым шумом падающего светового пучка. Таким образом, отношение сигнал/шум для усиленного выходного тока уменьшается по сравнению с таковым для входного тока не более чем в 2 раза.
В промежуточном случае, реализуемом, например, в кремнии, скорости ионизации для электронов в 10—100 раз больше, чем для дырок. В этих условиях вплоть до коэффициентов усилений порядка 10—100 такой переход ведет себя скорее как переход с умножением носителей одного типа. Процесс умножения хорошо поддается контролю и по своим свойствам приближается к умножению, свободному от шумов. В кремнии детектирование отдельных фотонов удалось осуществить с эффективностью примерно 10%. Используя кремниевый р — n-переход при обратном смещении, охлажденный до температуры жидкого воздуха, оказалось возможным достаточно близко подойти к режиму лавинного пробоя, и тогда в силу статистического характера процесса примерно 10% фотонов вызывали обнаруживаемые импульсы заряда.
↑ Умножение в изоляторах
Данные, свидетельствующие об ударной ионизации в материалах, которые являются изоляторами при комнатной температуре, то есть в материалах с шириной запрещенной зоны больше 2 эВ, почти отсутствуют. Исключение, вероятно, составляет фосфид галлия. Отсутствие прямых данных особенно удивительно, если вспомнить, что начиная с 30-х годов в большом количестве работ электрический пробой диэлектриков интерпретировался именно на основе ударной ионизации. Так, Уайтхед анализировал обширный экспериментальный материал, полученный по пробою диэлектриков, с помощью впервые предложенных Фрёлихом изящных теоретических моделей генерации «горячих» электронов в сильных полях. Более того, в случае щелочно-галоидных кристаллов, на которых были выполнены наиболее обстоятельные измерения (в частности, фон Хиппелем с сотрудниками), значения электрических полей, при которых происходит пробой, вычисленные с помощью теории электронно-фононного взаимодействия Фрёлиха, совпадают с соответствующими экспериментальными значениями с точностью до множителя 2. Уже благодаря одному этому факту в литературе глубоко укоренилось представление о связи пробоя диэлектриков с ударной ионизацией.
Несмотря на обилие косвенных данных, казалось бы позволяющих объяснить пробой диэлектриков ударной ионизацией, прямые экспериментальные доказательства существования электронов с достаточно высокими энергиями, которые должны быть ответственны за такую ионизацию, отсутствуют. В щелочно- галоидных кристаллах эти электроны должны были бы обладать энергией около 10 эВ, то есть порядка ширины запрещенной зоны, и легко наблюдаться по их эмиссии в вакуум. В то же время возрастает количество данных, указывающих на то, что пробой изоляторов скорее связан с определенным типом полевой эмиссии либо с электродов, либо с неких внутренних микротрещин. Вильяме сопоставил начало процессов полевой эмиссии и ударной ионизации в хлориде натрия и пришел к заключению, что при увеличении электрического поля прежде всего возникает полевая эмиссия. Подобные утверждения оказались справедливыми также для CdS и ZnO.
Наряду с работами по пробою диэлектриков существует также обширная литература по электролюминесценции сульфида цинка в переменном поле, где возбуждение центров люминесценции приписывается ударной ионизации. Однако и здесь большинство данных свидетельствует о том, что электролюминесценция в этих материалах связана главным образом с туннелированием (то есть с полевой эмиссией) электронов и дырок с микротрещин с острыми краями, имеющихся в мелких кристаллах. Однако, согласно некоторым другим данным, ударная ионизация реализуется при электролюминесценции, возбуждаемой постоянным полем. Механизм такой люминесценции еще не определен однозначно. В любом случае лишь небольшая доля электронов достигает энергии, достаточной для ударной ионизации.
Мы уже отмечали, что полевая эмиссия является сильным конкурентом процессу ударной ионизации. Но даже если удастся избежать полевой эмиссии, то все равно на пути контролируемого использования ударной ионизации существует еще одно препятствие, связанное с катастрофическим характером перехода в этот режим. Теория электронно-фононного взаимодействия в ионных твердых телах, разработанная Фрёлихом, предсказывает существование именно такого резкого порога для «горячих» электронов и ударной ионизации. Экспериментальные данные, полученные в основном путем исследования эффекта Ганна в арсениде галлия и других аналогичных материалах, подтверждают это заключение. Эффект Ганна представляет собой начальную стадию пробоя, при котором электроны прорываются через низкоэнергетический барьер, равный энергии оптического фонона (примерно 0,1 эВ), после чего энергия электронов перестает возрастать из-за наличия второго барьера, находящегося примерно на 0,5 эВ выше дна зоны проводимости; этим барьером служит расположенный выше дополнительный минимум зоны проводимости. Поскольку большинство изоляторов обладает ионным или полярным характером связи, следует ожидать, что пороги образования высокоэнергетических электронов в них слишком резкие, что препятствует использованию этих материалов в твердотельных умножителях.
Теоретическое рассмотрение ударной ионизации в сильных полях основано непосредственно на теории электронно-фононных взаимодействий в твердых телах. Такое рассмотрение, как правило, производится в рамках довольно сложного квантовомеханического формализма. Электроны и фононы рассматриваются как волны. Математические операции выполняются в Фурье-пространстве и включают сложные процессы интегрирования, за которыми трудно уловить физический смысл явлений. В следующем разделе мы попытаемся изложить основные черты электронно-фононных взаимодействий в реальном пространстве с помощью сравнительно простого математического аппарата. Физический механизм, определяющий скорость потерь энергии электронами больших энергий, в значительной степени поддается классическому описанию и легко может быть представлен наглядно.
Особое внимание мы уделим некоторым основным чертам процесса генерации высокоэнергетических электронов в сильных полях: различию между контролируемой природой процессов, связанных с «горячими» электронами в неполярных твердых телах, и резким началом аналогичных процессов в полярных твердых телах, оценке величины полей, необходимых для создания «горячих» электронов, согласно которой в материалах с более высокими изолирующими свойствами требуются более сильные поля, и, наконец, конкуренции между полевой эмиссией и ударной ионизацией.
↑ Скорости потерь энергии горячими электронами
Стабильные и нестабильные скорости потерь энергии. Сначала остановимся на простом критерии, определяющем возникновение «горячих» электронов. Для того чтобы электроны сохраняли энергию выше энергии дна зоны проводимости, они должны получать ее от поля с той же скоростью, с какой теряют ее отдавая решетке.
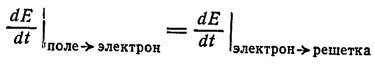
или
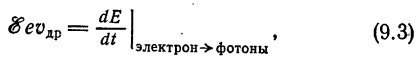
E — электрическое поле, vдр — дрейфовая скорость электронов в направлении поля.
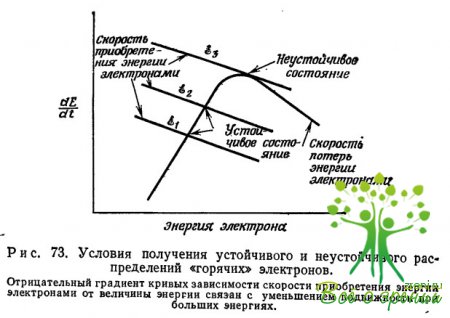
При заданном электрическом поле как левая, так и правая части соотношения (9.3) зависят от энергии электрона (первая — через vдр). Поэтому мы сразу же можем указать различные типы зависимостей, которые будут обеспечивать либо устойчивую, либо не¬устойчивую генерацию «горячих» электронов. Эти два предельных случая показаны схематически на рис. 73,
где E3>>E2>>E1. Для «устойчивых» точек пересечения E1 и E2 большее электрическое поле стабильно дает электроны с большей энергией. В случае «неустойчивого» пересечения, E3 ничто не мешает электрону приобретать произвольно высокие энергии, ограниченные в конечном счете лишь ударной ионизацией. Если потери энергии электронами вызваны их взаимодействием с акустическими и неполярными оптическими фононами, то мы получаем устойчивое пересечение; если же электроны отдают энергию полярным оптическим фононам, то пересечение оказывается не¬устойчивым.
Общий метод оценки скорости потерь энергии. Находясь в твердой (или конденсированной) среде, электрон возмущает ее вокруг себя. Он может поляризовать ее своим электрическим полем, может в результате пьезоэлектрического эффекта создавать механическое напряжение и может благодаря своему заряду привести к искажению структуры энергетических зон. Во всех этих случаях возникает энергия взаимодействия и вокруг электрона существует нечто вроде потенциальной ямы. Если электрон движется медленно, то он «тянет» потенциальную яму за собой. Если он движется быстро, то часть потенциальной ямы как бы отстает от него и движется за ним, как волна за кормой лодки. Эта картина действительно очень напоминает движение лодки в воде или самолета в воздухе. Энергия возмущения представляет собой энергию, теряемую движущейся частицей, будь то лодка, самолет или электрон.
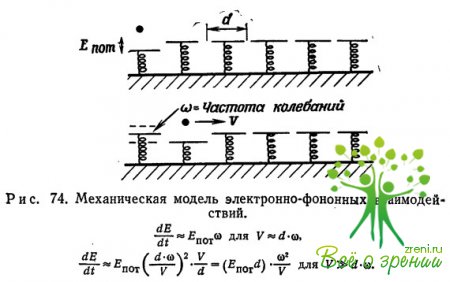
На рис. 74 показана простая механическая модель потерь энергии движущейся частицей.
Здесь частица проходит вдоль цепочки элементов размером d, обладающих характерной частотой ?. Между частицей и каждым элементом действует сила отталкивания, так что, когда частица неподвижна, она «отталкивает» ближайший элемент, в пружине которого таким образом запасается энергия Eпот.В этой модели частица, движущаяся со скоростью v, представляет электрон, элементы — среду, а энергия Eпот соответствует энергии взаимодействия электрона со средой.
С помощью рис. 74 можно оценить максимальную скорость потерь энергии при взаимодействии электрона со средой, она равна
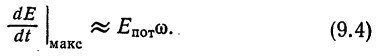
Такая скорость получается, если считать, что электрон находится против каждого элемента в течение времени ?-1, которое по определению есть время ответа элемента, или время, требуемое для образования потенциальной ямы Eпот. Затем электрон резко смещается к следующему элементу, оставляя за собой энергию Eпот. Там он снова остается в течение времени ?-1 и опять резко сдвигается к следующему элементу. Таким образом он излучает в среду энергию со скоростью Eпот*?. Вместо только что описанного дискретного движения (шаг за шагом) можно представить, что электрон движется со средней скоростью d*?, при которой он способен создавать в каждом элементе потенциальную яму. глубиной более поло-вины энергии Eпот и вместе с тем более половины энергии оставлять за собой в виде следа.
Чтобы получить более общее выражение для скорости потерь энергии, будем считать, что электрон движется со скоростью, превышающей d*?. Тогда он проходит мимо элемента за время, меньшее по сравнению с временем ответа, и,- следовательно, создает потенциальную яму, глубина которой составляет лишь часть энергии Eпот.
Импульс, передаваемый электроном элементу, уменьшается на величину d*?/v, определяемую отношением времени пролета к времени релаксации элемента. Энергия, которую электрон отдает элементу, пропорциональна квадрату импульса и поэтому уменьшается пропорционально (d*?/v)2. Тогда скорость потерь энергии мы запишем в виде
где Eпот*(d*?/v)2 — энергия, передаваемая электроном каждому элементу, а v/d — число элементов, которые он проходит за 1 с.
Учтем теперь, что электрон может передавать энергию среде только путем кулоновского взаимодействия . Максимальная энергия, отданная электроном среде, равна полной энергии кулоновского взаимодействия. В общем случае в зависимости от связи электрона со средой он передает ей только долю ? этой энергии, причем 0 ? ? ? 1. Следовательно, формально мы можем представить энергию взаимодействия Епот[sub] таким образом:

где е2/K*d — кулоновская энергия электрона, соответствующая расстоянию d, а К — диэлектрическая проницаемость для частот больших, чем частота излучения в среду ?. Для таких частот поляризационное облако, окружающее электрон, движется вместе с ним без потерь. Рассматривая потери энергии, связанные с фононами, мы будем понимать под К электронную часть диэлектрической проницаемости.
Из соотношений (9.5) и (9.6) мы получаем общее выражение, которое определяет потери энергии быстрыми электронами в твердом теле

Это выражение необходимо проинтегрировать по d. Такое интегрирование, вообще говоря, дает геометрический фактор порядка 1. При расчете потерь, связанных с полярными оптическими фононами, этот фактор равен
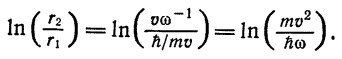
Здесь r[sub]2 есть расстояние по радиусу до элемента среды, за пределами которого среда при прохождении электрона поляризуется и деполяризуется без передачи энергии, а r1=h/m*v —«радиус» электрона, вычисленный из соотношения неопределенностей. При меньших радиусах электрон уже нельзя считать точечным зарядом, а следует рассматривать как заряд, распределенный по объему. Этот пример показывает, что физический механизм электронных потерь можно объяснить в рамках чисто классических представлений. Однако при количественном расчете этого классического взаимодействия следует учесть определенные квантовомеханические ограничения, например «радиус» электрона. Другое ограничение квантовомеханического характера заключается в том, что энергия электрона ?*m*v2 должна быть не меньше энергии испускаемого им кванта h*?.
Относительная простота и наглядность соотношения (9.7) позволили использовать его для анализа широкого спектра энергетических потерь электронов в твердых телах, начиная от потерь, связанных с фотонами, плазмонами, глубоко расположенными рентгеновскими термами, и кончая потерями на черенковское излучение. Здесь мы приведем лишь некоторые наиболее существенные результаты этого анализа. В табл. 2 различные выражения для энергетических потерь,
связанных с фононами, приведены в такой форме, где выделены константа связи ?, геометрический фактор и общее для всех выражений ядро е2?2/K*v.
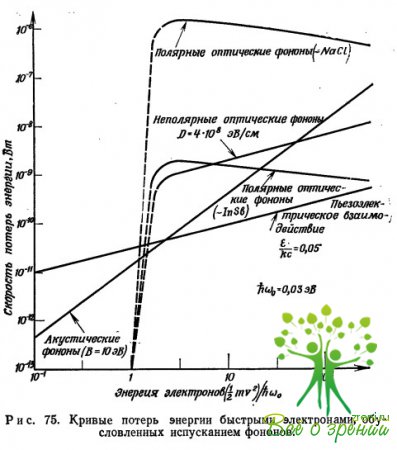
На рис. 75 представлена зависимость энергетических потерь электронов при взаимодействии с фононами различного типа от энергии электронов.
Сопоставление с рис. 73 показывает, что потери при взаимодействии с акустическими и неполярными оптическими фононами могут приводить к устойчивой генерации «горячих» электронов. Напротив, потери при взаимодействии с полярными оптическими фононами ведут к неустойчивому положению, в последнем случае приложенное поле сообщает электрону энергию со скоростью, превышающей ту, которая соответствует? максимуму кривой потерь. Величина этого поля равна
если m = m0 (масса свободного электрона) и ? = 1014 с-1; К0 и К? — низкочастотная и высокочастотная (электронная) диэлектрические проницаемости.
Для нас существенно то, что большинство изоляторов представляет-собой полярные материалы, в которых доминируют потери на полярные оптические фононы. Более того, константа связи (К0-K?)/K0, вероятно, близка к 1. Это означает, что поле, при котором происходит пробой, или, иначе, образование «горячих» электронов, по-видимому, должно превышать 106 В/см и приближаться к 107 В/см. При таких полях становится существенным конкурирующий процесс полевой эмиссии.
Константа связи в изоляторах, то есть материалах с большой шириной запрещенной зоны, близка к 1 по следующей причине. Разность К0 — К? характеризует вклад в диэлектрическую проницаемость, обусловленный смещениями ионов. Согласно теории и экспериментальным данным, он составляет 2 или несколько больше и не зависит от ширины запрещенной зоны. Электронная часть диэлектрической проницаемости зависит от ширины запрещенной зоны и уменьшается с ее увеличением. Это обусловлено тем, что в изоляторах валентные электроны связаны более сильно и труднее поляризуются приложенным полем. Поэтому коэффициент К0 — К?/К0 К? значительно возрастает по мере увеличения ширина запрещенной зоны. Его величина для NaCl в 100 раз больше, чем для InSb. Заметим также, что при вы-, воде соотношений (9.7) и (9.8) никак не учитывалась кристаллическая структура материала. Следовательно, поля, требуемые для получения «горячих» электронов в изоляторах, столь же высоки в аморфных материалах, как и в кристаллических. В действительности в первом случае поля могут быть даже несколько выше, так как вследствие аморфной структуры материала уменьшается подвижность электронов и тем самым скорость, с которой приложенное поле передает энергию электронам. При анализе энергетических потерь в аморфных материалах обычными формальными методами возникают значительные трудности, поскольку эти методы с самого начала предполагают периодичность решетки.
Теперь сопоставим напряженности полей, при которых возникает значительная полевая эмиссия, с таковыми для ударной ионизации [см. (9.8)]. На рис. 76 показан типичный барьер,
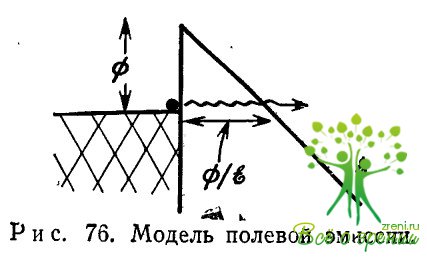
через который электрон туннелирует из металлического контакта в зону проводимости изолятора. Вероятность прохождения свободного электрона через такой барьер (или
где Ф — высота барьера (В), а E — напряженность поля (В/см). (Величина множителя в знаменателе не равна точно 2, она зависит от способа рассмотрения.) Значительная полевая эмиссия имеет место в том случае, когда показатель экспоненты составляет около 20. При этом прозрачность материала возрастает при-« мерно в 1010 раз при увеличении поля вдвое. Пользуясь этим критерием, находим критическую напряженность поля, при которой возникают инжекционные токи:
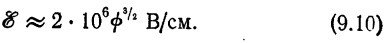
Совершенно такое же выражение справедливо для полевой эмиссии (туннелированне Зинера, зинеровский пробой) из валентной зоны в зону проводимости. Следовательно, если мы примем ф = 1 — 2 эВ, что соответствует изоляторам, то заметная полевая эмиссия начинается при полях (2—6)* 106 В/см. Величины полей, при которых возникает пробой в процессе ударной ионизации [см. (9.8)], лежат в том же интервале. Поэтому эти два эффекта часто трудно различить. Однако большинство данных свидетельствуют о том, что обычно причиной пробоя диэлектриков является полевая эмиссия.
Конкуренция между процессами полевой эмиссии и генерации «горячих» электронов особенно отчетливо наблюдалась в проведенной недавно работе по холодным эмиттерам, где поле прикладывали к тонкому изолятору, заключенному в структуру типа сандвич (металл—изолятор—металл). Здесь электроны туннелируют в зону проводимости изолятора с металлического катода. Сильное электрическое поле в изоляторе разогревает электроны, так что их средняя энергия достигает около 0,5 эВ, при этом небольшая часть (10-2—10-6) общего числа электронов обладает энергией, превышающей работу выхода тонкой металлической пленки анода, и может выйти в вакуум.
Существенно, что даже при напряженностях поля, соответствующих умеренному разогреву электронов, в результате полевой эмиссии из катода в изолятор уже идет значительный ток. Наличие экого большого темнового тока не позволяет использовать тонкие изолирующие пленки в твердотельных умножителях для передачи изображения слабо освещенных сцен.
Попытки создать твердотельные фотоумножители не принесли особых успехов. В умножителях, использующих полупроводниковые переходы на основе германия, кремния и арсенида галлия, удалось получить коэффициенты усиления примерно до 100. Из-за значительных темновых токов применение этих устройств ограничено передачей сигналов с большой скоростью при высоких интенсивностях света. В твердотельных изолирующих материалах добиться больших коэффициентов усиления пока не удалось.
Статья из книги: Зрение человека и электронное зрение А.Роуз 1977
.


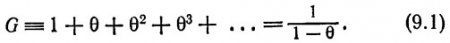
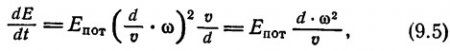

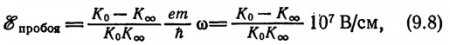
Комментариев 0