Геометрическая оптика

Описание
Действие очков на зрение основано на законах распространения света. Наука о законах распространения света и образования изображений с помощью линз называется геометрической, или лучевой, оптикой.
Великий французский математик XVII в. Ферма сформулировал принцип, лежащий в основе геометрической оптики: свет всегда выбирает кратчайший по времени путь между двумя точками. Из этого принципа следует, что в однородной среде свет распространяется прямолинейно: путь луча света из точки 81 в точку 82 представляет собой отрезок прямой. Из этого же принципа выводятся два основных закона геометрической оптики — отражения и преломления света.
ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
Если на пути света встречается другая прозрачная среда, отделенная от первой гладкой поверхностью, то луч света отчасти отражается от этой поверхности, отчасти проходит через нее, меняя свое направление. В первом случае говорят об отражении света, во втором — о его преломлении.
Чтобы объяснить законы отражения и преломления света, нужно ввести понятие нормали — перпендикуляра к отражающей или преломляющей поверхности в точке падения луча. Угол между падающим лучом и нормалью в точке падения называется углом падения, а между нормалью и отраженным лучом — углом отражения.
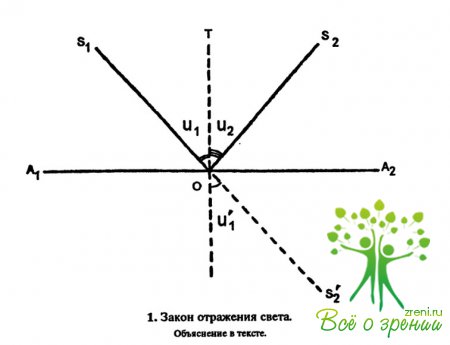
Закон отражения света гласит: падающий и отраженный лучи лежат в одной плоскости с нормалью в точке падения; угол падения равен углу отражения.
На рис. 1 показан ход луча между точками S1и S2при его отражении от поверхности А1А2. Перенесем точку S2в S2', находящуюся за отражающей поверхностью. Очевидно, линия S1 S2' будет кратчайшей, если она прямая. Это условие выполняется, когда угол u1=u1' и, следовательно, u1= u2, а также когда прямые OS1,ОТ и OS2 находятся в одной плоскости.
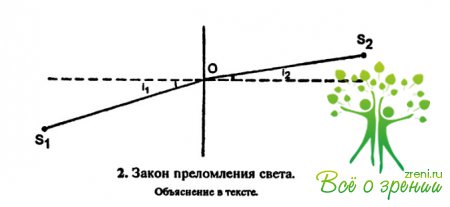
Закон преломления света гласит: падающий и преломленный лучи лежат в одной плоскости с нормалью в точке падения; отношение синуса угла падения к синусу угла преломления для данных двух сред и для лучей данной длины волны есть величина постоянная.
Не приводя расчетов, можно показать, что именно эти условия обеспечивают кратчайшее время прохождения света между двумя точками, находящимися в разных средах (рис. 2).
Закон преломления света выражается следующей формулой:
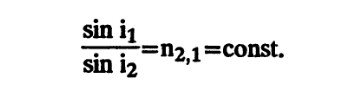
Величинаn2,1называется относительным показателем преломления среды 2 по отношению к среде 1.
Показатель преломления данной среды относительно пустоты (практически к ней приравнивают воздушную среду) называется абсолютным показателем преломления данной среды n.
Относительный показатель преломления n2,1связан с абсолютными показателями первой (n1) и второй (n2) среды отношением:
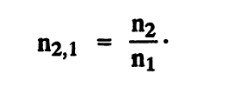
Абсолютный показатель определяется оптической плотностью среды: чем больше последняя, тем медленнее распространяется свет в данной среде.
Отсюда второе выражение закона преломления света: синус угла падения так относится к синусу угла преломления, как скорость света в первой среде к скорости света во второй среде:
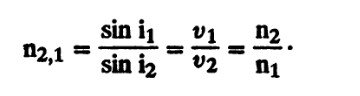
Поскольку свет обладает максимальной скоростью в пустоте (и в воздухе), показатель преломления всех сред больше 1. Так, для воды он составляет 1,333, для оптического стекла разных сортов — от 1,487 до 1,806, для органического стекла (метилметакрилата) —1,490, для алмаза— 2,417. В глазу оптические среды имеют следующие показатели преломления: роговица—1,376, водянистая влага и стекловидное тело —1,336, хрусталик —1,386.
ХОД ЛУЧЕЙ ЧЕРЕЗ ПРИЗМУ
Рассмотрим некоторые частные случаи преломления света. Одним из простейших является прохождение света через призму. Она представляет собой узкий клин из стекла или другого прозрачного материала, находящийся в воздухе.
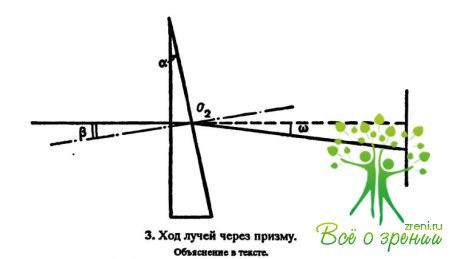
На рис. 3 показан ход лучей через призму. Она отклоняет лучи света по направлению к основанию. Для наглядности профиль призмы выбран в виде прямоугольного треугольника, а падающий луч параллелен его основанию. При этом преломление луча происходит только на задней, косой грани призмы. Угол w, на который отклоняется падающий луч, называется отклоняющим углом призмы. Он практически не зависит от направления падающего луча: если последний не перпендикулярен грани падения, то отклоняющий угол слагается из углов преломления на обеих гранях.
Отклоняющий угол призмы приблизительно равен произведению величины угла при ее вершине на показатель преломления вещества призмы минус 1:
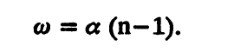
Вывод этой формулы следует из рис. 3. Проведем перпендикуляр ко второй грани призмы в точке падения на нее луча (штрихпунктирная линия). Он образует с падающим лучом угол ?. Этот угол равен углу ? при вершине призмы, так как их стороны взаимно перпендикулярны. Так как призма тонкая и все рассматриваемые углы малы, можно считать их синусы приблизительно равными самим углам, выраженным в радианах. Тогда из закона преломления света следует:
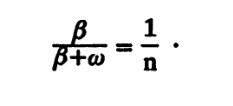
В этом выражении nстоит в знаменателе, так как свет идет из более плотной среды в менее плотную.
Поменяем местами числитель и знаменатель, а также заменим угол ? на равный ему угол ?:
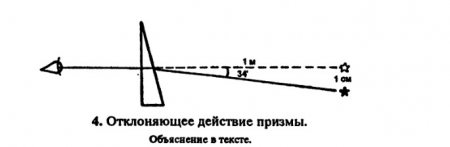
Поскольку показатель преломления стекла, обычно применяемого для очковых линз, близок к 1,5, отклоняющий угол призм примерно вдвое меньше угла при их вершине. Поэтому в очках редко применяются призмы с отклоняющим углом более 5°; они будут слишком толстыми и тяжелыми. В оптометрии отклоняющее действие призм (призматическое действие) чаще измеряют не в градусах, а в призменных диоптриях (?) или в сантирадианах (срад). Отклонение лучей призмой силой в 1прдптр (1 срад) на расстоянии 1 м от призмы составляет 1 см. Это соответствует углу, тангенс которого равен 0,01. Такой угол равен 34' (рис. 4).
Поэтому приближенно можно считать, что отклоняющее действие призмы в призменных диоптриях вдвое больше, чем в градусах (1прдптр = 1 срад ? 0,5°).
Это же относится и к самому дефекту зрения, косоглазию, исправляемому призмами. Угол косоглазия можно измерять в градусах и в призменных диоптриях.
ХОД ЛУЧЕЙ ЧЕРЕЗ ЛИНЗУ
Наибольшее значение для оптометрии имеет прохождение света через линзы. Линзой называют тело из прозрачного материала, ограниченное двумя преломляющими поверхностями, из которых хотя бы одна является поверхностью вращения.
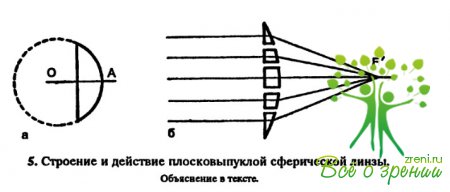
Рассмотрим простейшую линзу—тонкую, ограниченную одной сферической и одной плоской поверхностью. Такую линзу называют сферической. Она представляет собой сегмент, отпиленный от стеклянного шара (рис. 5, а). Линия АО, соединяющая центр шара с центром линзы, называется ее оптической осью. На разрезе такую линзу можно представить как пирамиду, сложенную из маленьких призм с нарастающим углом при вершине (рис. 5, б).
Лучи, входящие в линзу и параллельные ее оси, претерпевают преломление тем большее, чем дальше они отстоят от оси. Можно показать, что все они пересекут оптическую ось в одной точке (F'). Эта точка называется фокусом линзы (точнее, задним фокусом). Такую же точку имеет и линза с вогнутой преломляющей поверхностью, но ее фокус находится с той же стороны, откуда входят лучи. Расстояние от фокусной точки до центра линзы называется ее фокусным расстоянием (f'). Величина, обратная фокусному расстоянию, характеризует преломляющую силу, или рефракцию, линзы (D):
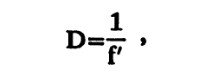
гдеD — преломляющая сила линзы, дптр; f' — фокусное расстояние, м;
Преломляющая сила линзы измеряется в диоптриях. Это основная единица в оптометрии. За 1 диоптрию (D, дптр) принята преломляющая сила линзы с фокусным расстоянием 1 м. Следовательно, линза с фокусным расстоянием 0,5 м обладает преломляющей силой 2,0дптр, 2 м —0,5 дптр и т. д. Преломляющая сила выпуклых линз имеет положительное значение, вогнутых — отрицательное.
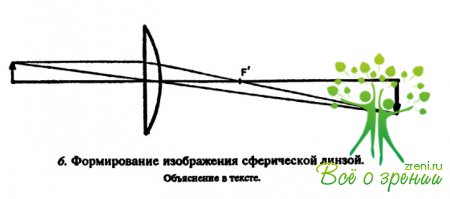
Не только лучи, параллельные оптической оси, проходя через выпуклую сферическую линзу, сходятся в одной точке. Лучи, исходящие из любой точки слева от линзы (не ближе фокусной), сходятся в другую точку справа от нее. Благодаря этому сферическая линза обладает свойством формировать изображения предметов (рис. 6).
Так же как плосковыпуклые и плосковогнутые линзы, действуют линзы, ограниченные двумя сферическими поверхностями,— двояковыпуклые, двояковогнутые и выпукло-вогнутые. В очковой оптике применяются главным образом выпукло-вогнутые линзы, или мениски. От того, какая поверхность имеет большую кривизну, зависит общее действие линзы.
Действие сферических линз называют стигматическим (от греч. — точка), так как они формируют изображение точки в пространстве в виде точки.
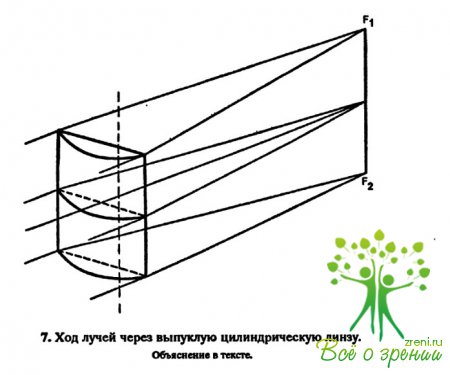
Следующие виды линз — цилиндрические и торические. Выпуклая цилиндрическая линза имеет свойство собирать падающий на нее пучок параллельных лучей в линию, параллельную оси цилиндра (рис. 7). Прямую F1F2аналогии с фокусной точкой сферической линзы называют фокальной линией.
Цилиндрическая поверхность при пересечении ее плоскостями, проходящими через оптическую ось, образует в сечениях окружность, эллипсы и прямую. Два таких сечения называются главными: одно проходит через ось цилиндра, другое — перпендикулярно ему. В первом сечении образуется прямая, во втором — окружность. Соответственно в цилиндрической линзе различают два главных сечения, или меридиана,— ось и деятельное сечение. Нормальные лучи, падающие на ось линзы, не подвергаются преломлению, а падающие на деятельное сечение, собираются на фокальной линии, в точке ее пересечения с оптической осью.
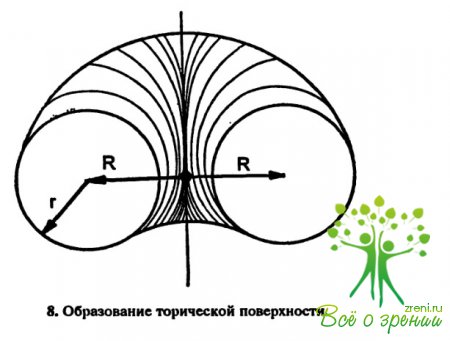
Более сложной является линза с торической поверхностью, которая образуется при вращении окружности или дуги радиусом rвокруг оси. Радиус вращения R не равен радиусу r(рис. 8).
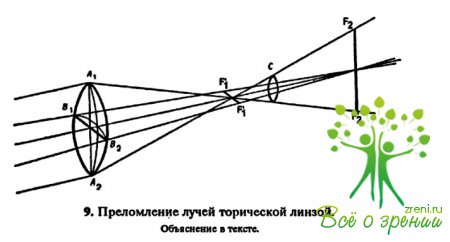
Преломление лучей торической линзой показано на рис. 9.
Торическая линза состоит как бы из двух сферических: радиус одной из них соответствует радиусу вращаемой окружности, радиус второй — радиусу вращения. Соответственно линза имеет два главных сечения (А1А2и В1В2). Падающий на нее параллельный пучок лучей преобразуется в фигуру, называемую коноидом Штурма. Вместо фокусной точки лучи собираются в два отрезка прямых, лежащих в плоскости главных сечений. Они называются фокальными линиями — передней (F1F1) и задней (F2F2).
Свойство преобразовывать пучок параллельных или идущих от точки лучей в коноид Штурма называют астигматизмом (буквально «бесточие»), а цилиндрические и торические линзы— астигматическими линзами. Мерой астигматизма является разность преломляющей силы в двух главных сечениях (в диоптриях). Чем больше астигматическая разность, тем больше расстояние между фокальными линиями в коноиде Штурма.
Астигматическим действием характеризуется и любая сферическая линза, если лучи падают на нее под большим углом к оптической оси. Это явление называют астигматизмом косого падения (или косых пучков).
В оптометрии приходится иметь дело еще с одним видом линз— с афокальными линзами. Афокальной называется такая линза, обе сферические поверхности которой имеют одинаковый радиус, но одна из них вогнутая, а другая выпуклая (рис. 10, а).
Такая линза не имеет фокуса и, следовательно, не может формировать изображение. Но, находясь на пути светового пучка, несущего изображение, она его увеличивает (если свет идет справа налево) или уменьшает (если свет идет слева направо). Такое действие афокальной линзы называется эйконическим (от греч. - изображение). Чаще для этого применяют не одиночные линзы, а их системы, например телескопы. На рис. 10, б, показана схема простейшего телескопа, состоящего из одной отрицательной и одной положительной линзы (система Галилея).
Эйконическое действие присуще и обычным сферическим линзам: положительные линзы увеличивают, а отрицательные — уменьшают изображение. Измеряют это действие в процентах, а при больших увеличениях — в «крагах» (х). Так, лупа, увеличивающая изображение в 2раза, называется двукратной (2х).
Таким образом, линзы осуществляют четыре вида оптического действия: призматическое, стигматическое, астигматическое и эйконическое. Далее будет показано, как все они используются для коррекции дефектов зрения.
Отметим, что в большинстве случаев для линз характерно не только, то действие, для которого они предназначены: сферическим (стигматическим) линзам присуще также и эйконическое действие, а на периферии стекла, кроме того, призматическое и астигматическое. Астигматические линзы характеризуются также стигматическим, призматическим и эйконическим действием.
СЛОЖНЫЕ ОПТИЧЕСКИЕ СИСТЕМЫ
До сих пор речь шла об идеальных линзах, как бы не имеющих толщины (за исключением афокальных). В оптометрии приходится иметь дело с линзами, имеющими реальную толщину, а еще чаще с системами линз.
Особый интерес представляют центрированные системы, т. е. такие, которые состоят из сферических линз, имеющих общую оптическую ось. Для описания таких систем и расчета их действия применяют два способа: с введением так называемых кардинальных точек и плоскостей; с использованием понятия сходимости лучей и вершинной рефракции.
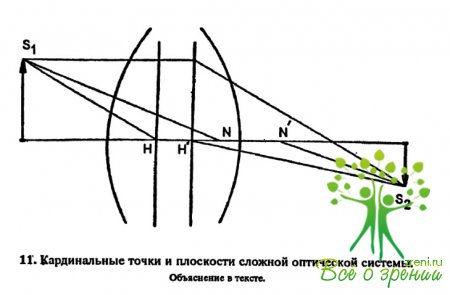
Первый способ, разработанный немецким математиком Гауссом, заключается в следующем. На оптической оси системы выделяют четыре Кардинальные точки: две узловые и две главные (рис. 11).
Узловые точки — передняя и задняя (Nи N') — обладают следующим свойством: луч, входящий в переднюю точку (S1N), выходит параллельно самому себе из задней (N’S2). Их применяют при построении изображений, формируемых оптической системой.
Гораздо большее значение имеют главные точки (Ни Н'). Перпендикулярные к оптической оси плоскости, проведенные через них, называются главными плоскостями — передней и задней. Луч света, входящий в одну из них, проходит до другой параллельно оптической оси. Иначе говоря, изображение на задней главной плоскости повторяет изображение на передней. Все расстояния на оптической оси отсчитывают от главных плоскостей: до объекта—от передней, до изображения — от задней. Часто эти плоскости лежат так близко друг к другу, что приближенно могут быть заменены одной главной плоскостью.
Так, например, в оптической системе человеческого глаза передняя главная плоскость лежит в 1,47 мм, а задняя — в 1,75 мм от вершины роговицы. При расчетах принимают, что обе они расположены приблизительно в 1,6 мм от этой точки.
Второй способ описания центрированных оптических систем предполагает, что пучку лучей в каждой точке на оптической оси присуще особое свойство — сходимость. Она определяется величиной, обратной расстоянию до точки схождения этого пучка, и измеряется, так же как и рефракция, в диоптриях. Действие каждой преломляющей поверхности на пути пучка— это изменение сходимости. Выпуклые поверхности увеличивают сходимость, вогнутые — уменьшают. Сходимость параллельного пучка лучей равна нулю.
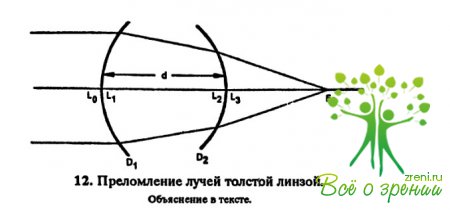
Этот способ особенно удобен для расчета суммарной преломляющей силы системы. Типичной сложной оптической системой является толстая линза (рис. 12), имеющая две преломляющие поверхности и однородную среду между ними.
Изменения сходимости падающего на линзу параллельного пучка лучей определяются преломляющей силой этих поверхностей, расстоянием между ними и показателем преломления материала линзы.
Примем следующие обозначения:
- L0— сходимость параллельного пучка, падающего на линзу;
- L1— сходимость пучка после преломления на первой поверхности линзы;
- L2— сходимость пучка при достижении второй поверхности линзы;
- L3— сходимость пучка после преломления на второй поверхности, т. е. при выходе из линзы;
- D1- преломляющая сила первой поверхности;
- D2— преломляющая сила второй поверхности;
- d— расстояние между поверхностями линзы;
- n— показатель преломления материала линзы.
При этом величины L иD измеряются в диоптриях, а d-b— в метрах.
Сходимость пучка на входе в линзу L0 = 0.
После преломления на передней поверхности ЛИНЗЫ она становится равной L1=D1. При достижении задней поверхности она приобретает значение:
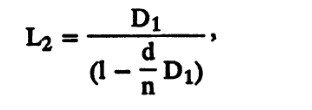
и, наконец, при выходе из линзы
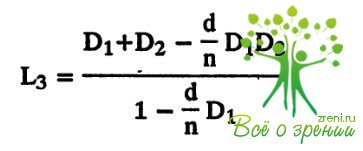
Это выражение показывает изменение сходимости пучка при прохождении через линзу при отсчете расстояний от ее передней поверхности. Оно называется передней вершинной рефракцией линзы. Если рассматривать ход лучей от задней поверхности к передней, то в знаменателе D1заменится на D2. Выражение
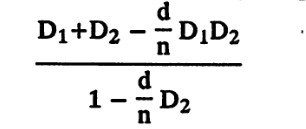
представляет собой величину задней вершинной рефракции толстой линзы. Значения силы линз в пробных наборах очковых стекол и представляют собой их задние вершинные рефракции.
Числитель этого выражения является формулой для определения суммарной преломляющей силы системы, состоящей из двух элементов (поверхностей или тонких линз):
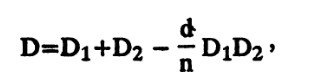
гдеD — суммарная преломляющая сила системы;
D1и D2— преломляющая сила элементов системы;
n— показатель преломления среды между элементами;
d- расстояние между элементами системы.
Статья из книги: Оптометрия | Розенблюм Ю.З..


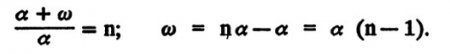
Комментариев 0