Свет и цвет

Содержание:
Описание
↑ Качество света
До сих пор мы говорили о способности глаза воспринимать световые воздействия, каждое из которых определяется одной скалярной величиной, прежде всего яркостью. Шкала яркостей располагается вдоль одной линии, яркостный контраст тоже одномерен. Однако в природе постоянно встречаются предметы одинаковой яркости, а тем не менее глаз хорошо отличает их друг от друга. Они отличаются по качеству отраженного от них света, по его спектральному составу, например зеленый лист и красная роза. Таким образом, кроме количественных характеристик света глаз воспринимает и различает его качественные характеристики. Объясняется это тем, что аппарат дневного зрения (колбочковый) имеет три приемника света с различной селективной чувствительностью. Условно их называют красным, зеленым и синим. Благодаря наличию этих селективных приемников глаз способен ощущать не только яркость, но и цветность предмета. Цветность в свою очередь тоже сложное понятие. Красная роза может быть насыщенно красной, а может быть и розовой, т. е. бледно-красной. Слово «красный» приближенно определяет то, что в науке о цветовых измерениях — колориметрии — называют цветовым тоном излучения, а уточнение «бледно» характеризует малую насыщенность или, если применить колориметрический термин, малую чистоту цвета. Итак, цвет можно определить тремя величинами: яркостью L, цветовым тоном ?, чистотой цвета р. Монохроматическое излучение любой области спектра обладает чистотой р, равной единице. Примесь белого понижает р, и для белого цвета р = 0. Но пока нам важно одно: цвет полностью может быть определен тремя числами.
Вскоре мы увидим, что для определения цвета можно избрать и другие величины, но их должно быть обязательно три, что соответствует трем приемникам излучения в сетчатке. Три величины можно считать координатами в трехмерном пространстве и любой цвет — точкой в нем. Совокупность всех возможных— реальных — цветов заполнит некоторый объем, образуя так называемое цветовое тело.
↑ Система RGB
Основные величины, характеризующие цвет, можно выбрать такими, что цвет получит свойства вектора, а это значительно упростит колориметрические расчеты. Чтобы с цветом можно было обращаться, как с вектором, за три координаты следует принять три цвета и считать их основными в рассматриваемой системе. Познакомимся прежде всего с системой RGB, в основу которой положены три цвета, соответствующие монохроматическим излучениям с длинами волн 700; 546,1 и 435,8 нм. Любой другой цвет представлен как вектор в пространстве с составляющими r', g' и b' по осям координатной системы R, G и В соответственно, т. е.
где Ц — вектор цвета; R, G, В — единичные векторы основных цветов.
Экспериментально найти эти координаты любого цвета Ц или, иначе говоря, измерить цвет Ц можно с помощью колориметра. Колориметр — усложненный фотометр, на одно из полей которого подается излучение измеряемого цвета Ц, а на другое— смесь основных излучений R, G и В. Меняя интенсивности основных излучений смеси, добиваются визуального равенства обоих полей по яркости и цветности, т. е. по цвету. Получают координаты измеряемого цвета, т. е. составляющие вектора, длина которого характеризует яркость, а направление в пространстве — цветность.
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
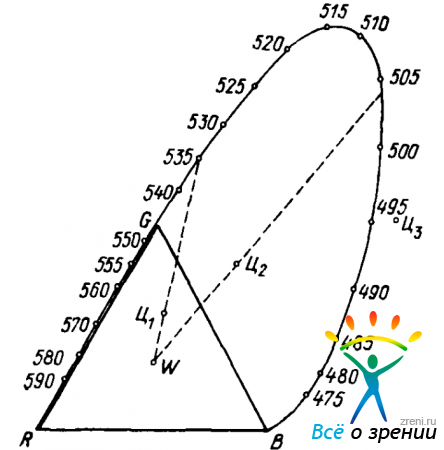
Отложим на осях R, G и В единичные векторы R, G и В и проведем плоскость через концы этих трех векторов. Мы получим треугольник (рис. 39), на вершинах которого лежат точки R, G, В. Координаты любого единичного вектора получим по формулам
из которых ясно, что
и что, следовательно, цветность - величина двухмерная, ибо определяется только двумя независимыми переменными. Цветность— точка на плоскости, изображенной на рис. 39.
Рис. 39. Плоскость единичных цветов
Стороной треугольника RB и опирающейся на нее кривой очерчена область реально существующих цветностей. Лежащая в центре треугольника точка W есть цветность белого равноэнергетического излучения (источник Е). Яркости единичных цветов, казалось бы, проще всего положить равными друг другу н равными, скажем, 1 кд/м2. Однако оказалось, что при смешении трех цветов с одинаковыми яркостями получается отнюдь не белый, а голубой цвет. Чтобы получить белый цвет Е, приходится брать красного больше, чем синего, а зеленого еще больше, чем красного. Это неравенство можно перенести на единицы цветов и считать яркости единичных цветов такими: L(R) = 683 кд/м2; L(G)= 3135 кд/м2; L(B) = 41 кд/м2. Деля яркости единичных цветов на 683 кд/м2 (коэффициент, введенный для упрощения некоторых расчетов), получаем для каждого из основных цветов его яркостный коэффициент: LR = 1; LG = 4,59; LB = 0,06.
Яркость цвета Ц с координатами r', g' и b' можно рассчитать по формуле
Яркость L любого цвета Ц равна сумме яркостей составляющих его цветов, а длина вектора Ц равна сумме его координат. Это положение как будто противоречит основам векторного исчисления: длина вектора не равна сумме его составляющих. Но здесь все дело в переменном масштабе измерения: длина единичного вектора зависит от его направления.
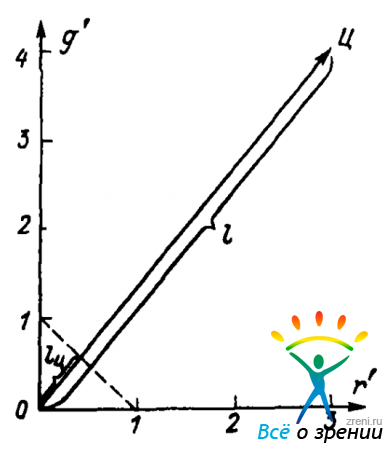
Операции с такими векторами не так уж сложны, по все же несколько тяжеловесны. Однако, чтобы понять суть дела, достаточно рассмотреть хотя бы один конкретный пример. Предположим, у нас есть цвет Ц с координатами (рис. 40)
Рис. 40. Пример сложения векторов цвета
r' = 3, g' = 4, b' = 0. Вектор Ц в данном случае лежит в плоскости R, G.
Если бы 3 и 4 были просто единицами длины, l равнялось бы 5. Но проведем между точками r' = 1 и g' = 1 прямую (след плоскости единичных векторов) и получим длину отрезка lц — длину единичного вектора цвета Ц. Легко убедиться простым отсчетом, что l = 71ц. Перенос задачи из плоскости в пространство (b' ? 0) по существу ничего не меняет.
↑ Цветность
Двухмерная диаграмма цветности наглядно изображается плоскостью единичных векторов (рис. 39). Чтобы получить на этой диаграмме цветность любого цвета Ц, достаточно предположить, что в точках R, G и В подвешены грузы, пропорциональные координатам цвета r', g' и b', а затем найти центр тяжести системы. Поставленная на диаграмме точка центра тяжести изображает цветность цвета Ц.
Пусть нам дан цвет Ц1 с координатами r' = 0,27; g'= 0,90; b' = 0,40. На плоскости рисунка 39 он изображается точкой Ц1. Проведем через точки W и Ц1 прямую и продолжим ее до линии спектральных цветов. Мы попадаем в точку ? — 535 нм. Значит, цвет Ц1 зеленый. Но точка Ц1 лежит близко к точке W. Следовательно, чистота цвета Ц1 мала. Он похож на белый и только слегка зеленоват.
Теперь рассмотрим цвет Ц2 с координатами r' = —0,22; g' = — 0,90; b' = 0,50. Его цветовой тон ? = 504 нм (тоже зеленый, но другого оттенка). Но что означает отрицательная координата? Дело в том, что смешением трех основных цветов системы RGB можно получить только цвета, лежащие внутри треугольника RGB. Смешением можно получить цвет любого цветового тона, но чистота цвета при смешении уменьшается. Это уменьшение почти незаметно в длинноволновой области спектра (сторона треугольника RG) и очень сильно для зеленых и синих цветов.
А что физически означает отрицательная координата? Если на одно поле колориметра подан цвет Ц2, на другое нужно подать составляющие g' и b'. А составляющую r' в количестве 0,22 нужно подать на поле измеряемого цвета.
Рис. 39 позволяет легко находить для любого цвета дополнительный цвет, т. е. получать пару цветов, которые при смешении (в строго определенной пропорции) дают белый цвет W. Так, например, к голубому цвету с ? = 490 нм дополнительным будет оранжевый (? = 600 нм).
Но многие цвета не имеют спектрально-чистых дополнительных: так, напрнмер, прямая, проведенная от ? — 535 нм через W, упирается в сторону RB. Тут лежат пурпурные цвета, которых нет в спектре. Их обычно характеризуют длиной волны дополнительного к ним цвета.
↑ Система XYZ
Отрицательные координаты многих цветов в системе RGB вызывают некоторые неудобства при колориметрических расчетах. Однако простым изменением выбора основных цветов этого недостатка устранить нельзя. В системе RGB взяты за основу спектрально чистые цвета, а смешение снижает их чистоту. Следовало бы взять за основу цвета с чистотой, большей, чем у спектральных цветов, по таких в природе не существует. Взглянем, например, на точку Ц3 на рис. 39. Она изображает некий цвет, который имеет определенные составляющие в системе RGB. Коордниаты его r’ = — 0,35; g' = 0,34; b' = 0,34. Но таких цветов в природе нет. Они лежат вне области реальных цветов. Это цвета нереальные.
Однако нереальные цвета имеют чистоту, большую, чем у спектральных (или у чистых пурпурных — линия RB), и ими можно воспользоваться для формальных математических преобразований. Выбрав за основные три нереальные цвета, можно построить систему, в которой все реальные цвета будут иметь только положительные координаты. Такая система построена. Это международная система XYZ. Все три основные ее цвета X, Y и Z — цвета нереальные. Зато любой реальный цвет в системе XYZ имеет только положительные координаты. Остававшаяся большая свобода выбора основных цветов позволила наложить на них еще некоторые условия. Как и в системе RGB, при равенстве координат х' = у' = z' получается белый равноэнергетический цвет. Кроме того, вся яркость цвета сосредоточена в одной координате Y. Яркостные коэффициенты системы: Lx = 0; Lz = 0; Ly = 1.
↑ Колориметрические расчеты
Цвет любого излучения — непосредственно идущего от источника, или прошедшего сквозь фильтр, или рассеянного поверхностью предмета — можно не только измерить колориметром, но и вычислить, если известен спектральный состав излучения.
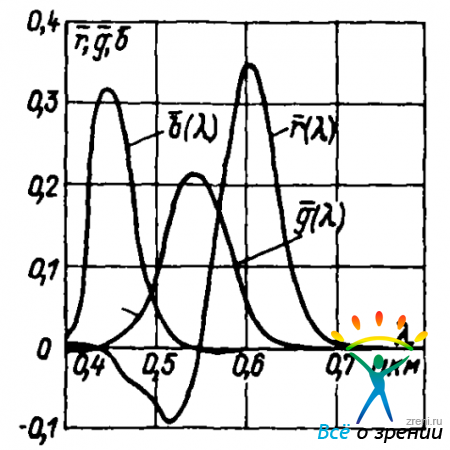
В 1931 г. на VIII сессии МКО была принята Система RGB и утверждены кривые сложения (см. рис. 41),
Рис. 41. Кривые сложения системы RGB
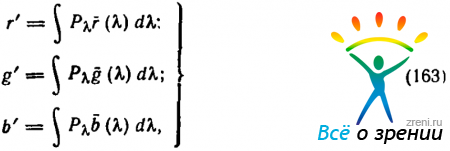
которые лежат в основе пересчета спектрального состава в цвет по формулам
где Р?—спектральная плотность мощности излучения, a r-(?), g-(?) и b?(?) — удельные координаты спектральных излучений, показанные на рис. 41.
С официальным принятием такого метода пересчета спектрального состава цвет стал уже объективной физической величиной, независимой от индивидуальных свойств глаза.
От чего же зависит цвет окружающих нас предметов? От спектрального распределения коэффициентов отражения р(?) и ст спектрального состава падающего света Р'?. При вычислении цвета поверхности предмета в формулах (163) следует сделать подстановку Р? = Р'?р (?).
В специальных книгах по колориметрии развит довольно сложный математический аппарат для всевозможных колориметрических расчетов. Мы хотели здесь показать только основные их принципы, сделав их по возможности наглядными.
↑ Цветовые пороги
Часто считают цвет тела некоторой постоянной, присущей ему характеристикой: лист зеленый, апельсин оранжевый и т. д. Это неверно. Цвет тела зависит от спектрального состава освещающего его света. Но хотелось бы, чтобы он не зависел от интенсивности освещения.
Этого можно достигнуть, если одной из координат цвета тела сделать не яркость, а коэффициент отражения поверхности тела р. В системе XYZ яркость полностью характеризуется координатой у'. Все три координаты цвета можно нормировать, исходя из условия у' = р. Приняв во внимание, что коэффициент отражения не может превышать ста процентов, получим условие у' ? 100. Соответственно конечные значения приобретают и другие координаты х' и z', и все цветовое тело в такой системе получает конечный объем.
Хотя число точек — различных цветов — и в такой системе остается бесконечным, но конечным можно считать число различаемых цветов. Если разница в цветовых координатах двух соседних цветов меньше некоторой пороговой величины, мы не можем отличать один цвет от другого.
Возьмем два близких, едва различимых цвета Ц0 и Ц1 Пороговая разность этих векторов ?Ц1 тоже вектор. Кроме цвета Ц1 имеется еще множество цветов Цi, которые едва отличимы от цвета Ц0. Вокруг Ц0 образуется геометрическое место концов всех векторов ?Цi — поверхность, ограничивающая объем цветов, не отличимых от Цо. Дело обстояло бы не так уж сложно, если бы все векторы ?Цi были равны по модулю, т. е. пороговая поверхность была бы сферой. Но пи в одной из упомянутых нами систем это условие не соблюдается. Можно, хотя и приближенно, считать пороговую поверхность трехосным эллипсоидом с полуосями Ах', А у', А z'.
Сделано несколько попыток так преобразовать колориметрическую систему, чтобы во всех областях цветового тела равным расстояниям между двумя точками соответствовало равное число пороговых различий цвета. На этом принципе создано несколько систем, называемых равноконтрастными. Однако все они выполняют предъявляемое к ним требование весьма приближенно.
Сколько же цветов может различать глаз во всем объеме цветового тела? Сколько-нибудь точного ответа на этот вопрос мы дать не можем. Ограничимся грубой оценкой. Сделаем ее в наиболее наглядной системе: р — коэффициент отражения; ?— цветовой тон; р — чистота цвета. В работе число градаций яркости приближенно определяется по формуле
где К — пороговый (по яркости) контраст. Положив К = 0,03, получим m = 120. Пороговые различия по цветовому тону в разных местах спектра различны. Минимальное значение ?? = 1 нм. Но так как для многих участков спектра и пурпурных тонов ?? значительно больше, можно принять, что всего глаз способен различать 150 цветовых топов.
Число градаций чистоты цвета в среднем можно считать равным 15. Перемножив эти три числа, получим для всего количества различаемых цветов внушительную величину — 270 000. Это число, видимо, сильно преувеличено, так как на самом деле цветовые пороги по одной координате зависят от других координат. Но реально созданные атласы цветов, в которых различия между соседними цветами значительно больше пороговых, показывают, что различимых глазом цветов очень много: в атласе Менселла 1200 цветов, в атласе Научно-исследовательского института имени Д. И. Менделеева 2000.
Таким образом, цветовое зрение во много раз увеличивает получаемую нами информацию: вместо сотни ступеней яркостных различий нами воспринимаются тысячи различий в цвете предметов.
----
Статья из книги: Глаз и свет | Луизов А.В.


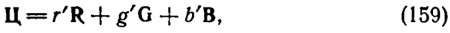

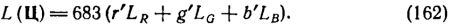

Комментариев 0