Моделирование патогенеза начальной близорукости на основе рефракционной биомеханики глаз (Часть 1)

Описание
Предмет математического моделирования патогенеза начальной близорукости на основе рефракционной биомеханики глаз. В настоящее время математическое моделирование занимает все большее место в биологических и медицинских исследованиях.Математические модели биологических объектов и процессов можно классифицировать по выделенным Н. В. Тимофеевым-Ресовским (1975) уровням организации живой природы: молекулярно-генетический, онтогенетический, популяционно-видовой, биосферный. В то же время необходимо расширять исследования на онтогенетическом уровне, создать более детальные модели на уровне организма — моделирование функционирования различных систем органов, а также отдельных органов и тканей (А. А. Ляпунов, Г. П. Багриновская, 1975).
Математические модели этого уровня ближе всего к медицинским задачам. Одним из основных источников математических моделей в биофизике органов и организма остается механика. В связи с этим для прогресса в создании математических моделей функционирования органов необходимо ускоренное развитие биомеханики, основателем ряда разделов которой являлся еще Леонардо да Винчи. Биомеханику определяют, как раздел биофизики, изучающий механические свойства живых тканей и органов, а также механические явления, происходящие в них в процессе жизнедеятельности.
В ряде случаев чисто биомеханический подход не раскрывает полностью сущности исследуемых явлений, поэтому современная математическая модель функционирования (или нарушения функционирования) какого-либо органа должна, во-первых, основываться на «кибернетической биомеханике», во-вторых, учитывать данные о структуре живых тканей на молекулярном уровне.
В офтальмологии недостаточно развит тот уровень моделирования, который связан с биомеханикой глаза. Рассматриваемые ниже модели относятся к рефракционной биомеханике глаза. Термин «рефракционная биомеханика» впервые нами предложен в 1974 г. Систематические работы по рефракционной биомеханике в офтальмологической литературе до 1973 г. практически отсутствовали.
Под рефракционной биомеханикой следует понимать раздел биомеханики глаза, который изучает процессы, приводящие к изменениям рефракции или сопровождающие эти изменения. Изучение этих процессов необходимо для углубления наших знаний о происхождении видов рефракции, в частности близорукости.
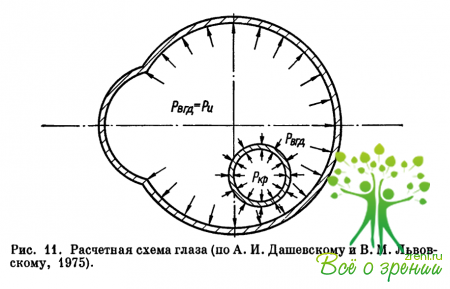
Применение теории оболочек для исследования ВГД. В работе (1975) А. И. Дашевский и В. М. Львовский приводят расчетную схему глаза (рис. 11), в которой склера представлена в виде заполненной жидкостью тонкостенной сферической оболочки, а кровеносные сосуды — одним тонким цилиндром, расположенным внутри глаза и испытывающим с наружной стороны давление Рвгд и с внутренней стороны — давление Ркр. Принято, что часть кровяного давления уравновешивается упругими силами стенок сосудов, а другая часть передается на внутриглазную жидкость и создает давление на склеру. Противодавление склеры приводит к возникновению ВГД. Предположение о том, что ВГД порождается мышечной энергией сердца, высказывали А. И. Дашевский (1946), Gloster (1967).
По сравнению с состоянием, когда ВГД отсутствует, склеральная оболочка растянута. Если обозначить ее радиус R, толщину — б, а упругие напряжения - ?, то в простейшем случае (отсутствие каких-либо внешних сил) ДЛЯ сферической оболочки ? = PR/2?, где Р — некоторое внутреннее давление.
В этом случае обобщенным законом Гука для склеры является выражение
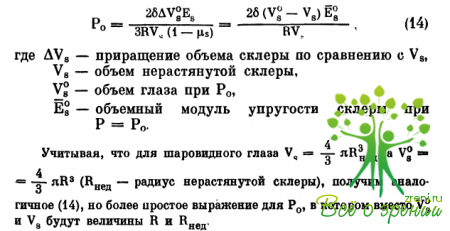
где Еs — модуль упругости склеры, µs — ее коэффициент Пуассона, ?Vs — приращение объема склеры по сравнению с объемом Vs (объем при Р = 0), ?s — объемный модуль упругости склеры (назван так в отличие от известного модуля объемной упругости или объемной деформации К = Е/3 * (1-2µ), ?s — объемная деформация склеры.
Из двух приведенных выражений для о видно, что

Тонометр сжимает роговицу глаза и перемещает некоторый объем внутриглазной жидкости внутрь склеральной оболочки. ВГД при этом повышается. В живом глазу под действием смещенного объема жидкости происходит растяжение склеры и сжатие кровеносных сосудов.
В офтальмологии известна формула Фриденвальда, связывающая изменение объема при тонометрии с ВГД. А. И. Дашевский и В. М. Львовский показали, что для выполнения формулы Фриденвальда необходимо, чтобы объемный модуль упругости склеры ?s изменялся по экспоненциальному закону

где ?ts — объемный модуль упругости склеры при тонометрическом давлении Рt,
?su — начальный (исходный) модуль упругости склеры,
Ks — коэффициент, соответствующий коэффициенту ригидности склеры в формуле Фриденвальда,
?s — объемная деформация склеры.
В живом глазу необходимо учитывать также и роль сосудов. В стенках сосудов радиусом Rc и толщиной ?с возникает напряжение
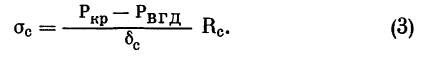
С учетом продольных напряжений обобщенный закон Гука для сосудов можно записать так:
где ? — коэффициент, зависящий от силы сопротивления току крови,
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
Ec — модуль упругости сосудов,
µс — коэффициент Пуассона для них,
?Vc — приращение объема крови в них по сравнению с объемом Vc (объем при Р = 0),
?с — объемный модуль упругости сосудов,
?c — объемная деформация сосудов.
Из (3) и (4) видно, что
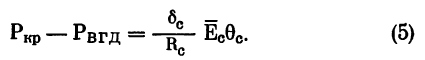
Объем крови в сосуде равен объему самого сосуда, то есть VKP = Vc + ?Vc. Объем Vkp растягивает сосуд и изменяет его объем на ?Vc,кр. Последнюю величину можно определить по формуле Фриденвальда, а из выражения для ?Vc,кр = Vкр найти Рвгд.
По А. И. Дашевскому и В. М. Львовскому (1975), ВГД определяется параметрами склеры и сосудов и диастолическим давлением крови:
Известно, что при повышении Pкр от диастолического (Ркд — 35 мм рт. ст.) до систолического (Ркс — 65 мм рт. ст.) ВГД лишь незначительно изменяется (на 1—2 мм рт. ст.).
При синусоидальном изменении давления крови
где Т — период пульсации крови. Величина ?c должна также изменяться по гармоническому закону для обеспечения постоянства ВГД.
Если же считать, что

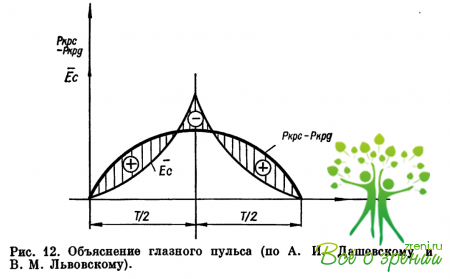
где обозначения аналогичны обозначениям в формуле (4), то получает объяснение существование незначительного глазного пульса. Оно основано на том, что при одновременном выполнении условий (7) и (8) возрастание Ес в один отрезок времени меньше разности Ркс — Ркд, а в другой—больше (рис. 12). Величину Ес можно определить также по данным скорости распространения по сосудам пульсовой волны (Н. Рашевски, 1966), причем King (1947) разработал соответствующую теорию и для случая, когда стенка сосуда не подчиняется закону Гука.
Деформации склеры при конвергенции и моделирование конвергентного повышения ВГД. Изменение мышечного равновесия глаз при переводе взгляда на близкое расстояние (физиологическая экзофория для близкого расстояния) является следствием временного удлинения глаза во время конвергенции при его деформации в мышечной воронке (А. И. Дашевский, 1973). Возникающую при этом временную осевую миопию автор назвал конвергентной миопией.
Одним из важных биомеханических последствий конвергентного удлинения глаза является конвергентное повышение ВГД. Экспериментально конвергентное повышение ВГД было впервые исследовано сотрудниками Днепропетровской глазной клиники (А. И. Дашевский, 1973; C. Г. Кривенков, 1973; А. И. Дашевский, С. Г. Кривенков, 1974). Теоретически конвергентное повышение ВГД впервые было изучено нами (С. Г. Кривенков) в 1973 г. В связи с микродвижениями глаз при зрительной работе на близком расстоянии конвергентное повышение ВГД носит колебательный, толчкообразный характер (JI. А. Дымшиц, 1970; А. И. Дашевский, 1973; Comberg, 1954); оно является одним из важных факторов, способствующих переходу ложной миопии в осевую (А. И. Дашевский, 1968, 1973; С. Г. Кривенков, 1973; А. И. Дашевский, С. Г. Кривенков, 1974).
Условия для начала деформации склеры при конвергенции. В той части склеры, к которой не прилежат мышцы, ВГД уравновешивается только упругими силами склеры, так как глаз находится в состоянии динамического равновесия. Там же, где к поверхности глазного яблока прилежит наружная прямая мышца, ВГД уравновешивается как упругими силами склеры, так и перпендикулярной к поверхности склеры составляющей силы натяжения мышцы, что можно назвать внешним давлением мышцы на склеру.
Поскольку для данного угла конвергенции а ВГД одинаковое во всем глазу, на оба рассматриваемых нами участка поверхности склеры в соответствии с известным законом Паскаля действует изнутри одинаковая сила. Так как в обоих случаях ВГД уравновешено, естественно, что на участке, к которому прилежит мышца, упругие силы в склере меньше. Независимо от нас А. П. Нестеров (1973, 1974) также отметил, что упругие напряжения в склере зависят не от ВГД, а от разности давлений на обе поверхности склеры.
При увеличении угла конвергенции площадь прилегания к глазу наружной прямой мышцы увеличивается. При этом увеличивается как сила натяжения наружной прямой мышцы, так и величина ее внешнего давления на склеру. Упругие силы склеры на участке прилегания уменьшаются. При каком-то вполне определенном угле конвергенции ?0 наступит момент, когда ВГД на участке прилегания к глазу наружной прямой мышцы будет уравновешено только внешним давлением последней. Если теперь еще больше увеличить натяжение мышцы, склера начнет деформироваться.
Величина ?0 зависит, таким образом, от величины внешнего давления, необходимого для уравновешивания ВГД (или «замены» других сил на участке прилегания). Внешнее давление мышцы в свою очередь зависит от многих факторов. Величина производимой ею деформации растет при дальнейшем увеличении угла конвергенции.
Конвергентное повышение ВГД. А. И. Дашевский и В. М. Львовский (1975) выразили известную формулу Фриденвальда для здоровых глаз следующим образом:
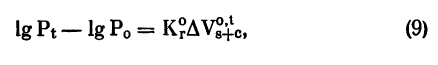
где Р0 — ВГД до тонометрии (оптические оси глаз параллельны, то есть ? = 0), Рt — ВГД в момент тонометрии,
?Vo,t ~ объем деформации роговицы, равный сумме объема растяжения склеры и объема сжатия сосудов, Кor — коэффициент реактивности глаза, различный для Р0 и Рt.
Принципиальных физических различий между воздействием на роговицу кружка сплющивания тонометра при тонометрии и воздействием на склеру при конвергенции наружной прямой мышцы нет. Следовательно, при ?>?0
где ?V?0,? — объем деформации той части склеры, к кото рой прилегает наружная прямая мышца, компенсирующийся растяжением остальной части склеры и сжатием сосудов,
Р? — ВГД при конвергенции на угол ?,
Р?0 — ВГД при конвергенции на угол ?0.
Это аналог формулы Фриденвальда, но для конвергенции, а не для тонометрии. Величину ?Vo,t благодаря простой форме деформации роговицы легко вычислить, а величину ?V?0,? определить трудно. Следовательно, неизвестен пока и точный вид зависимости ВГД при конвергенции от угла конвергенции. Несмотря на это, из формулы (10) видно, что при ? > ?0, Р? > Р?0, то есть наблюдается конвергентное повышение ВГД.
Рассмотрим вновь ту часть поверхности склеры, к которой не прилежат мышцы. Так как ВГД возросло, должны возрасти и упругие силы склеры для уравновешивания этого возросшего давления. А. И. Дашевский и В. М. Львовский (1975) действительно показали (для тонометрии), что логарифм объемного модуля упругости склеры пропорционален объемной деформации склеры (см. формулу 2). О таком увеличении упругих напряжений в склере в результате роста ВГД после деформации глаза наружными мышцами пишет и А. П. Нестеров (1973), хотя он ограничивается только качественными соображениями.
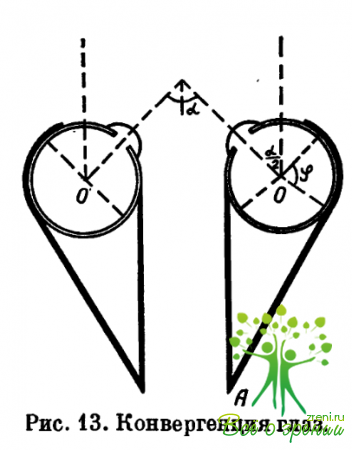
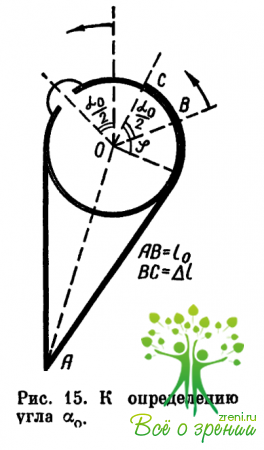
Определение критического угла конвергенции при котором начинается деформация склеры. Угол, под которым видна часть поверхности склеры, к которой прилежит наружная прямая мышца из центра глаза, обозначим через ? (рис. 13). Тогда площадь прилегания мышцы к глазу приблизительно равна R?a, где а—ширина мышцы в месте прикрепления ее к глазу и R?—длина дуги прилегания (R—радиус склеры, угол ф выражен в радианах).
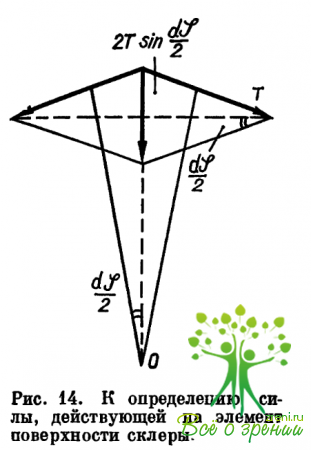
Выделим теперь бесконечно малый элемент участка прилегания; растягивающая этот элемент поверхности склеры сила, обусловленная ВГД, равна
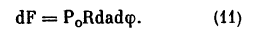
Обозначим силу натяжения мышцы через Т. Ее нормальная составляющая, действующая на элемент поверхности склеры, равна 2dT sin(d?/2) (рис. 14). Условие начала деформации для элемента поверхности склеры запишется так (ВГД уравновешивается только внешним давлением мышцы):
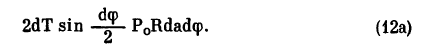
Пусть Еm — модуль упругости наружной прямой мышцы, b — ее толщина в месте прикрепления к глазу, l — длина мышцы при конвергенции на искомый угол ? (рис. 15), l0 — ее длина до конвергенции, 1нед — длина мышцы в недеформированном состоянии (то есть когда она отделена от глаза). Тогда по закону Гука
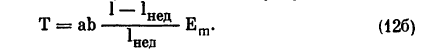
Из (12а) и (12б) после несложных преобразований (С. Г. Кривенков, 1973) находим величину ?0 (угол ?0 выражен в радианах):
Формула (13) дает выражение для ?0 через физические параметры глаза и наружной прямой мышцы.
Как показали А. И. Дашевский и С. Г. Кривенков (1974), величину ?0 можно выразить не только через параметры мышцы, но и через параметры склеры. Из предложенной А. И. Дашевским (1964 математической модели ВГД следует, что истинное ВГД зависит от ряда факторов следующим образом:
А. И. Дашевский и В. М. Львовский (1975) обосновали экспоненциальную зависимость объемного модуля упругости склеры ?о,s от модуля упругости нерастянутого склерального контура Еs. Такая же зависимость должна сохраняться и при анализе формулы (14). С учетом всего сказанного выражение для величины Р0 можно записать таким образом:
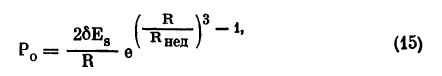
где е — основание натуральных логарифмов.
Подставив значение Р0 из выражения (15) в формулу (13), получим выражение для угла а0 через физические параметры склеры и наружной прямой мышцы:
Учет действия на склеру косых мышц (при конвергенции). При каком-то вполне определенном угле конвергенции р косые мышцы начинают деформировать склеру. Рассмотрим ту часть склеры, к которой прилежит одна из косых мышц. Пусть ? > mах (?0?), то есть и наружная прямая мышца, и рассматриваемая косая мышца деформируют глаз. Если области деформаций не перекрываются, что для не очень больших деформаций справедливо, действие на склеру каждой из мышц можно рассматривать независимо от действия другой. Каждая из мышц будет вызывать изменение ВГД.
Сравнивая (17) и (18), окончательно получим, что
Для упрощения рассуждений можно считать, что ?0 < ? то есть что наружная прямая мышца начинает деформировать глаз раньше, чем косые мышцы. Это позволяет применять полученную нами численную оценку для Еm в качестве основы для обсуждения результатов измерения BГД при конвергенции.
Результаты измерения ВГД при конвергенции. В настоящее время в Днепропетровской глазной клинике на-коплен экспериментальный материал, подтверждающий выводы о конвергентном повышении ВГД и существовании угла ?0, сделанные на основании приведенных выше математических закономерностей.
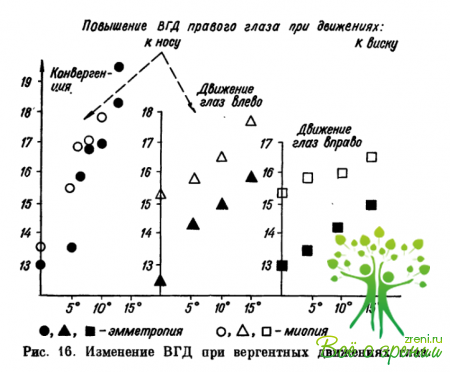
Т. А. Комлева и А. И.Шевцова измеряли ВГД при конвергенции при следующих расстояниях точки фиксации от обоих глаз: 5 м, 33 см, 25 см, 20 см, 16,7 см, 12,5 см. Измерения производили тонометром Дашевского. Исследованы 209 человек — 74 с нормальным зрением и 135 лиц со спазмом аккомодации (при ложной или истинной миопии). Средняя величина ВГД для указанных выше расстояний составила (рис. 16) соответственно 13; 13,5; 15,9; 16,9; 17; 18 и 13,4; 15,6; 16,8; 16,9; 17,9; 19,4 мм рт. ст. Эти данные могут считаться экспериментальным доказательством наличия спазма абдукторов при ложной миопии, что подтверждает одно из положений конвергентно-аккомодационно-гидродинамической гипотезы происхождения и развития близорукости.
Конвергентное повышение ВГД у лиц, страдающих близорукостью, большее, чем у эмметропов, за счет меньшей величины угла ?0 для близоруких глаз. Величина ?0 может уменьшаться как в результате увеличения Еm, так и за счет уменьшения толщины склеры ? и ее объемного модуля упругости ?s. При развитии миопии могут иметь место оба эти процесса, что заметно уменьшает ?0.
Увеличение Еm мы связываем со спазмом абдукторов. Уменьшение величин ? и Еm объясняется происходящими в склере близоруких глаз глубокими структурными изменениями. Наиболее детальные электронномикроскопические исследования этих изменений были проведены Т. Э. Николаевой (1973, 1974); Однако структурные изменения в склере важны для уточнения механизмов прогрессирования миопии средней и высокой степеней. В рамках рефракционной биомеханики глаз шаровидной формы можно рассматривать только эмметропию и разные стадии ложной миопии. При ложной миопии изменения в склере еще несущественны и главной причиной уменьшения величины ? является увеличение Еm при спазме экстраокулярных мышц.
Рассматривая деформацию склеры при конвергенции, необходимо иметь в виду, что в эмметропических глазах она является временной, обратимой и существует лишь тогда, когда глаза конвергируют. В этих условиях конвергентное повышение ВГД является нормой, а не патологией.
О том, что конвергентное повышение ВГД имеет прямое отношение к патологически соотношениям при миопии, свидетельствуют не только материалы Днепропетровской глазной клиники, но и работы по измерению коэффициента ригидности склеры (по А. И. Дашевскому — коэффициент реактивности живого глаза, то есть Кr, а не Ks). Как известно, коэффициент ригидности склеры уменьшается при повышении ВГД. Это было показано в работах Rethy (1965), Luyckx (1967),-Zolog, Chercota, Koos (1969).
Модуль упругости экстраокулярных мышц и его роль при конвергенции глаз. В 1973 г. нами был проанализирован механизм начала деформации глазных яблок и повышения ВГД при конвергенции. В частности, была получена формула для определения некоторого «критического» угла конвергенции а0, при котором склеру начинает деформировать наружная прямая мышца [см. формулу (13)]. По данным различных авторов (Sachsenweger, 1966), параметры наружной прямой мышцы имеют для человеческого глаза в среднем следующие значения: толщина b — 0,4 мм, длина в недеформированном состоянии 1нед — 38,5 мм, длина до конвергенции l0 — 45,8 мм.
Среднее значение радиуса склеры (R) близко к 12 мм. Среднее значение Р0 — 15 мм рт. ст. Неизвестна лишь величина Еm.
Максимально возможный угол конвергенции 90°, что соответствует приближению тест-объекта к глазам на расстояние порядка 3 см от линии их центров. Подставив в полученную (13) формулу для определения Еm, получим следующий результат:
который можно использовать для численной оценки Еm. В частности, подставляя в (20) значение ?0 = 0 и ?0 = ?/2 (что соответствует максимальной конвергенции), получим, что при 0 < ?0 0,32 • 107 дин/см2 угол ? < 0. Это означает, что глаз начнет деформироваться на участке прилегания к нему наружной прямой мышцы не при конвергенции, а при дивергенции. Если же Еm < 0,14 . 107 дин/см2, наружная прямая мышца вообще не деформирует глазное яблоко при конвергенции. Так как упругость мышцы у разных людей может значительно вариировать, рассмотренные случаи имеют место в практике. Таким образом, в зависимости от величины Еm изменяются условия начала деформации склеры и повышения ВГД, а следовательно, и условия перехода ложной миопии в осевую у лиц со спазмом аккомодации. Поэтому экспериментальное определение нормы для величины Еm представляет не только биометрический и теоретический, но и клинический интерес. Ниже анализируются результаты прямого измерения модуля упругости мышцы (С. Г. Кривенков и В. И. Лымарь, 1974).
Исследовано 12 наружных прямых мышц глаз, взятых от трупов. Перед опытом измеряли длину и поперечные размеры мышцы. Затем использовали методику, позволяющую определить Еm в состоянии мышечного тонуса, которому соответствовала бы средняя степень упругости мышцы (С. Г. Кривенков, В. И. Лымарь, 1974). Упругие свойства мышцы исследовали с помощью прибора, позволяющего определить изменение длины мышцы с точностью до 0,01 мм при дозированной весовой нагрузке (точность до 0,01 г). В пределах нагрузок, не вызывающих остаточных деформаций, для каждой мышцы производили несколько измерений с различными нагрузками. По ним вычисляли среднее значение Еm для данной мышцы. Затем было найдено среднее значение Еm для 12 исследованных мышц, которое оказалось равным приблизительно 0,37 * 107 дин/см2.
Если Еm больше 0,32 .107 дин/см2, это означает, что глазное яблоко на участке прилегания к нему наружной прямой мышцы начинает деформироваться не при конвергенции, а уже при дивергенции. Следовательно, и при отсутствии конвергенции, когда угол поворота равен нулю, такой глаз не является интактным. Его склера несколько деформирована, а ВГД выше, чем при наличии менее упругой мышцы. Как показывают описанные измерения Еm, эта величина у многих людей превосходит 0,32 * 107 дин/см2. По данным тонометрии, у ряда лиц с нормальной остротой зрения и у большинства страдающих миопией ВГД с увеличением конвергенции достаточно равномерно повышается, начиная с угла конвергенции, равного нулю! Такой характер повышения ВГД соответствует нормальному или повышенному модулю упругости мышцы.
Увеличение Еm при миопии связано со спазмом абдукторов, который, как уже говорилось, сопутствует спазму аккомодации. В то же время иногда ВГД начинает повышаться лишь после превышения определенного критического угла конвергенции, что, очевидно, соответствует слегка пониженному значению Еm. Таким образом, результаты измерений модуля упругости наружных прямых мышц подтверждают сделанные ранее теоретические предположения о характере деформации склеры при конвергенции и позволяют объяснить данные тонометрических исследований.
Автофокусировка глаз и ее связь с биомеханическим моделированием патогенеза миопии и лечебными оптикорефлекторными методами. О наличии зрительно-моторной цепи обратной связи известно достаточно давно. В процессе зрительного восприятия перемещающегося объекта происходит, по сути дела, сравнение его ожидаемой и действительной позиций. Их несовпадение порождает сигнал ошибки, возбуждающей аксоны моторной коры.
Упрощенная схема зрительно-моторной цепи обратной связи приведена в книге С. Дейча (1970), посвященной моделированию нервной системы. Для практических задач, в том числе и выдвигаемых офтальмологией, необходимо более детальное знание механизмов, обеспечивающих четкое восприятие перемещающихся объектов.
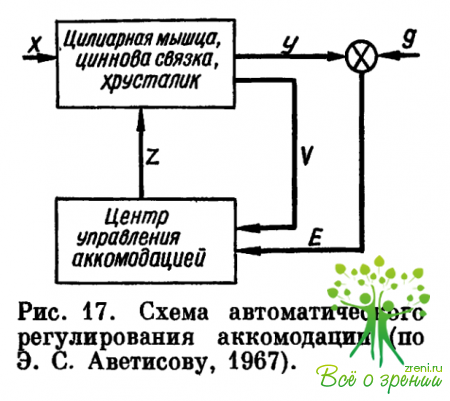
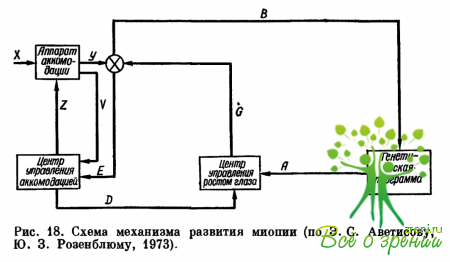
Э. С. Аветисовым (1967—1976) предложена схема, иллюстрирующая механизм аккомодации с позиций теории автоматического регулирования (рис. 17). Она принципиально верна, но недостаточна для объяснения методов воздействия на аккомодацию и для правильного понимания нейрофизических процессов, приводящих к саморегулированию аккомодации как к одному из проявлений автофокусировки глаз. Автор предложил и схему механизма развития миопии (рис. 18).
Ее можно признать верной, только если все механизмы рефрактогенеза имеют монокулярный характер, хотя в этом случае она. остается излишне упрощенной, если учесть наличие в ней гипотетического центра управления ростом глаза и «адаптационного» характера удлинения последнего при развитии миопии. По мнению А. И. Дашевского, механизмы рефрактогенеза в основном бинокулярны. На этой концепции автором основаны и разработаны методы лечения ЛОЖНОЁ миопии, нашедшие широкое практическое применение. В монографии Э. С. Аветисова и Ю. 3. Розенблюма «Вопросы офтальмологии в кибернетическом освещении» (1973) приведена схема управления механизмом формирования рефракции, отличающаяся от первой схемы только формальным учетом роли генетического фактора.


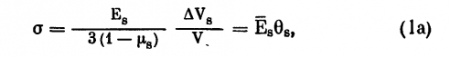
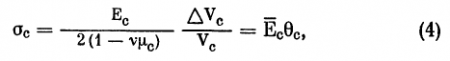
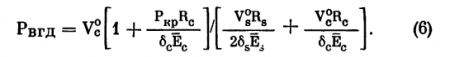
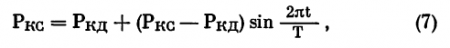

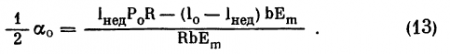
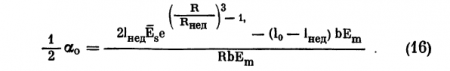

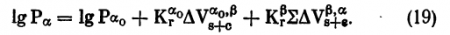
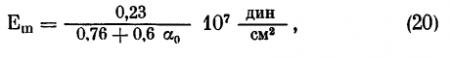
Комментариев 0