МАТЕМАТИЧЕСКАЯ ПСИХОФИЗИОЛОГИЯ ЦВЕТОВОГО ЗРЕНИЯ | Теория и модель в науке

Описание

Когда феноменология (результаты наблюдений или опытов) представлена в количественном выражении в виде графиков, таблиц или уравнений, в качестве языка можно использовать математику и соответственно строить математическую теорию.

Частным случаем теории является модель, которая позволяет проверить один или несколько аспектов теории путем конкретизации (обычно упрощающей) некоторых фундаментальных положений, лежащих в основании теории. Модель выполняет две важнейшие функции: компактного представления накопленных данных и рабочей гипотезы. После того как модель построена и следствия из нее выведены, она подвергается экспериментальной проверке. В науке известно два основных типа полезных моделей: отвергающие и развивающие теорию.

Например, модель дихроматического зрения, построенная на основе трехкомпонентной теории цветового зрения, предсказывает, что дейтеранопы в связи с потерей зеленочувствительного приемника из всего набора тонов спектра сохраняют в своем зрении только синие и красные тона и теряют голубые, зеленые, желтые и оранжевые, т. е. те, которые формируются за счет участия зеленочувствительного приемника. Это предсказание вступает в противоречие с экспериментальными данными, которые показывают, что у дейтеранопов как раз желтые тона сохраняются, а красные, наоборот, пропадают.
[banner_centerrs] {banner_centerrs} [/banner_centerrs]

В данном случае модель дихроматического зрения выступает в роли отвергающей теорию модели. Однако выявленное моделью рассогласование теории и эксперимента не обязательно отвергает теорию полностью, оно может быть связано с отдельными ее положениями, которые необходимо отвергнуть или изменить так, чтобы модельные результаты согласовывались с экспериментальными.

В нашем примере дефект трехкомпонентной теории содержится в положении об одностадийной структуре цветового зрения, т. е. представлении, что информация от трех рецепторов поступает непосредственно в систему порождения образа цветового восприятия. Изменив это положение введением второй стадии переработки информации (стадии оппонентных механизмов), можно согласовать теорию и эксперимент с помощью новой модели. В данном случае модель дихроматического зрения будет включать пострецепторный блок красно-зеленого и сине-желтого оппонентных каналов переработки информации, и в такой модели трехкомпонентная теория не будет отвергаться.

Более того, оказывается, что такая модель дихроматического зрения одним из своих следствий будет иметь новый тип дихроматизма (так называемую тетартонопию), существование которой экспериментальными исследованиями ранее обнаружено не было, а определилось только после теоретических разработок. В таких случаях модель дихроматического зрения будет развивать теорию, дополнять ее новыми следствиями и выводами, т. е. она будет относиться к развивающим теорию моделям.

Кроме полезных моделей нередко в науке встречаются и бесполезные, так называемые модели ad hoc .(от лат. к случаю). Остроумный вариант такого типа моделей придумал Пост. Представим себе фермера, предлагает Пост, который хочет сделать в ограде деревянную калитку. Его интересует, какой длины должно быть диагональное крепление I при определенной, длине основания х и высоте у калитки.

Он умеет измерять длины предметов, но не подозревает о существовании теоремы Пифагора, предполагая в этой связи, что в прошлом этот фермер был специалистом по колориметрии. Пытаясь выяснить, как связаны между собой длины элементов калитки, он придумывает следующую модель:

Обоснование своей модели он видит в совпадении некоторых общих соотношений между свойствами реальных длин и характеристиками модели. В частности, при увеличении длины основания или высоты калитки длина диагонального элемента увеличится, и это учитывается моделью. Далее, при х = 0, или у = О, I будет равно длине оставшейся стороны калитки и т. д.

Но, как только он пытается вычислить в модели по длинам сторон длину диагонали, он каждый раз получает некоторое расхождение между расчетом и практически требуемой длиной. В калитке диагональ почему-то всегда меньше. И вот, чтобы объяснить расхождение между своей моделью и реальными измерениями, фермер вводит новый феномен «сокращение калитки» и включает этот феномен в свою модель:

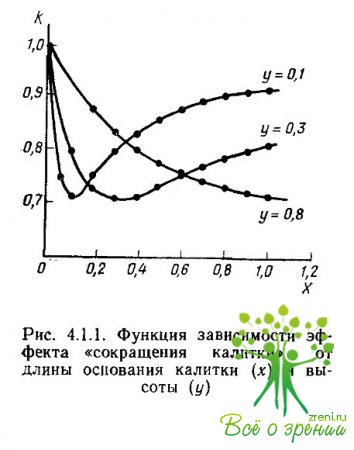
Исследуя свойства k, фермер устанавливает, что k не просто меньше или равно единице, а представляет собой довольно сложную функцию от х и у (рис. 4.1.1). Построив распределения коэффициента k от х и у, фермер со спокойной душой считает проблему решенной.

Можно представить себе его разочарование, когда он попытается применить эту модель для расчетов калитки не прямоугольной, а, например, трапециевидной формы. Один из верных способов избежать моделей фермерского типа — это включать в структуру модели как можно большее число различных феноменов.

Модель одного феномена — это практически всегда решение ad hoc. Но еще важнее добиваться содержательной интерпретации всех характеристик модели, избегая математических структур, которые не переводятся на язык психофизиологических феноменов. Особенностью психофизиологических моделей является то, что они должны объединить в себе и психофизические закономерности, и нейрофизиологические механизмы.

Психофизиологическая модель строится из нейроноподобных элементов таким образом, чтобы на выходе всей модели получать психофизиологические зависимости. При этом каждый нейроноподобный элемент модели должен воспроизводить реакции реального нейрона, участвующего в осуществлении моделируемой функции.

Проверка психофизиологической модели осуществляется путем построения предсказанных на основе модели психофизических закономерностей и характеристик тех реальных нейронов, которые были постулированы в модели. При подтверждении модели она используется для новых предсказаний. При ее расхождении с опытом модель модифицируется так, чтобы она охватывала всю совокупность экспериментальных данных.

Математические модели цветового зрения, которые будут рассматриваться в последующих разделах, принадлежат к категории полезных моделей.