Стереопсис. Часть 2.

Описание
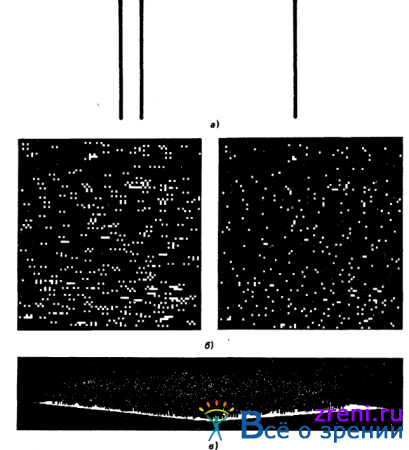
Процесс установления соответствий между изображениями стереопары. Выбор исходного представления приводит к алгоритму установления соответствий между изображениями стереопары, работа которого проиллюстрирована рис. 3.13Рис. 3.13. Решение для случайной конфигурации точек с 50 %-ным заполнением В верхней части рисунка представлены левое и правое изображения. Ниже в прямоугольной проекции представлены три карты диспаратности, построенные при установлении соответствий между описаниями пересечений нулевого уровня, приведенных на рис 3.14. Точка изображения с координатами (х, у) и приписанным ей значением диспаратности d представляется в этой трехмерной системе как точка с координатами (х, у, d) Таким образом, высота светлой точки над плоскостью указывает ее значение диспаратности
и 3.14.
Рис. 3.14. Результаты процедур свертки и определения пересечений нулевого уровня для стереограммы, представленной на рис 3.13. В двух левых столбцах сверху вниз приведены результаты свертки левого и правого изображений с фильтром с рецептивными полями размером w2-D = 35, 17 и 9 соответственно. В двух правых столбцах представлены пересечения нулевого уровня, полученные на основе результатов процедуры свертки, приведенных в двух левых столбцах. Обратите внимание на то, насколько больше подробностей выявляют рецептивные поля меньших размеров
На них приведены результаты обработки на ЭВМ (работа выполнена Э. Гримсоном) пары стереограмм, образованных случайными конфигурациями точек — такие стереограммы являются одним из наиболее трудных для данного алгоритма видов представления исходных данных.
Левое и правое изображения, составляющие стереограмму, образованную случайными конфигурациями точек и имеющую плотность заполнения 50%, приведены в верхней части рис. 3.13. Первый шаг данного алгоритма состоит в применении ?2 G-фильтра с большим рецептивным полем к каждому из этих изображений и определении пересечений нулевого уровня. Хотя теоретически элементы изображений, между которыми должно устанавливаться соответствие, включают как пересечения нулевого уровня, так и концы, лишь первые порождают трудности, связанные с ложными целями. Так, на рис. 3.14 представлены лишь пересечения нулевого уровня, причем горизонтальные отрезки фактически игнорируются, поскольку простыми средствами процесс установления соответствия для них реализовать не удается.
Для пересечений нулевого уровня помимо их местоположений задаются также знак и приблизительная ориентация. Этот знак характеризует знак изменения контраста при переходе через пересечение нулевого уровня слева направо и определяется уровнем серого тона, который на изображении соответствует пересечению нулевого уровня. Между двумя пересечениями нулевого уровня можно устанавливать соответствие, если у них одинаковые знаки и их локальные ориентации отличаются не более чем на 30°. Собственно процесс установления соответствия осуществляется вдоль пересечений нулевого уровня поточечно.
На рис. 3.14 приведены результаты свертки и пересечения нулевого уровня (со знаками), полученные при использовании ?2 G-фильтров с рецептивными
полями трех различных размеров. Читатель имеет возможность убедиться в том, что канал с наименьшим рецептивным полем дает значительно больше пересечений нулевого уровня, чем канал с наибольшим рецептивным полем. Это значит, что при использовании каналов с большими рецептивными полями диапазон рассматриваемых значений диспаратности можно увеличить, не рискуя одновременно увеличить частоту встреч с ложными целями.
Следовательно, рис. 3.13 и 3.14 дают возможность составить представление об общей структуре алгоритма. Вначале процесс установления соответствий реализуется на изображениях, обработанных фильтром с большим рецептивным полем; результаты этого шага алгоритма приведены на рис. 3.13, а, представляющем собой итоговую карту диспаратности, изображенную в прямоугольной проекции. Эти первые приближенные результаты служат исходными данными для того же самого процесса установления соответствия, но уже для канала с рецептивным полем среднего размера. Уменьшение допустимого диапазона значений диспаратности приблизительно компенсируется объемом информации, полученной благодаря использованию канала с большим рецептивным полем. Затем строится карта диспаратности, приведенная на рис. 3.13, б. Далее применяется канал с малым рецептивным полем, небольшой диапазон значений диспаратности которого позволяет получать точные значения диспаратностей; соответствующие результаты приведены на рис 3.13, в. В данном примере диспаратность центрального квадрата составляет 12 пикселов, а размер каждого черного квадрата — соответственно 4X4 пикселов. В итоговой карте диспаратности соответствие установлено неверно менее чем у 0,1 % точек, причем все они расположены на границах квадрата.
Еще о свойствах пересечений нулевого уровня. Данный алгоритм проблему ложных целей решает обходным путем, однако представляет интерес, как именно это делается, что очень важно с точки зрения психофизики. Мы не будем приводить здесь доказательства, но общую линию можно изложить и не вдаваясь в особые технические детали.
Основную идею иллюстрирует рис. 3.15.
Рис. 3.15. Пересечения нулевого уровня при переходе отрицательной полуволны чисто синусоидального сигнала в положительную полуволну (или при переходе положительной полуволны в отрицательную) обязательно разделены промежутком ?, где ? - длина волны
Допустим, что яркость изображения изменяется строго синусоидально, образуя вертикально ориентированную синусоидальную дифракционную решетку. Фурье-преобразование такого сигнала приведено на рис. 3.15, а. Этот сигнал не изменяется, пройдя через ?2 G-фильтр (его одномерное поперечное сечение приведено на рис. 3.15, б). Поскольку теперь задача сводится к установлению соответствий между пересечениями нулевого уровня для двух подвергнутых фильтрации изображений, допустим, что мы остановились на некотором конкретном пересечении нулевого уровня, принадлежащем левому изображению и соответствующем переходу от отрицательной к положительной полуволне синусоиды. Правильное соответствие для этого нулевого уровня обозначено на рис. 3.15, б через М. В таком случае F1 и F2 обозначают ложные цели. Так как, однако, они также должны представлять переход от отрицательной к положительной полуволне синусоиды, их следует разделить по меньшей мере расстоянием ?, где ? — длина синусоидальной волны. Итак, при условии ограничения поиска допустимых соответствий диапазоном значений диспаратности, не превышающим значения ?, имеется гарантия, что мы встретим лишь одно допустимое соответствие, и если какие-то иные средства позволяют нам приблизительно определять область, в которой следует вести поиск, то можно быть уверенным в том, что то единственное соответствие, которое будет нами обнаружено, является правильным.
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
Такова основная идея, но разнообразие реального мира не сводится к синусоидальной дифракционной решетке. Синусоидальная волна — это просто предельный случай функции с ограниченным спектром, в котором ширина полосы частот равна нулю. Приведенные выше качественные рассуждения сохраняют силу и при более широкой полосе частот, в чем в первом приближении можно убедиться, обратившись к рис. 3.16.
Рис. 3.16. В некотором диапазоне сигнал изменяется случайным образом (а). После прохождения через ?2 G-фильтр он принимает другой вид (б), причем пересечения нулевого уровня имеют более или менее регулярный характер Аналогичный пример для идеального однооктавного полосового фильтра приведен на рис. 2.19. При прохождении сигналов с ограниченным спектром через ?2 G-фильтр или идеальный однооктавный фильтр получаемые пересечения нулевого уровня, в среднем, не могут располагаться ни слишком близко, ни слишком далеко друг от друга. Интервалы, разделяющие пересечения нулевого уровня, подчиняются статистическим закономерностям, которые иллюстрируются рис. 3.17.
Рассмотрим, в частности, идеальный однооктавный полосовой фильтр, результат применения преобразования Фурье. Среднее значение такого сигнала равно нулю, и, следовательно, сигнал пересекает нулевой уровень достаточно часто, подобно тому как это происходит в случае синусоидальной волны. Поскольку, однако, спектр этого сигнала ограничен, его пересечения нулевого уровня не могут отстоять достаточно далеко друг от друга. Их частота, в среднем, соответствует среднему значению полосы частот фильтра.
Для нас же важно то обстоятельство, что пересечения нулевого уровня, в среднем, не могут располагаться слишком близко друг к другу, причем это справедливо для любого полосового фильтра. Однако ?2 G-фильтр также является лишь некоторой аппроксимацией полосового фильтра — читатель может убедиться в этом, если не сочтет за труд вновь обратиться к одномерному преобразованию Фурье этого фильтра. На рис. 3.16, б представлены результаты применения ?2 G-фильтра к случайному одномерному сигналу (рис. 3.16, а); очевидно, что этот сигнал после фильтрации обладает теми же качественными характеристиками, что и сигнал, приведенный на рис. 3.15, его среднее значение равно нулю, а пересечения нулевого уровня располагаются не слишком далеко и не слишком близко.
Общая идея доказательства теперь совершенно ясна — она в точности соответствует идее доказательства, относящегося к случаю синусоидальной волны. Поскольку ?2 G-фильтр представляет собой некоторую аппроксимацию полосового фильтра, пересечения нулевого уровня сигнала на его выходе обычно разделены некоторым минимальным расстоянием. При условии, что нам приблизительно известно, где именно следует искать соответствие, и при условии, что поиск не должен охватывать чрезмерно большой диапазон, мы сможем обнаружить единственного кандидата на соответствие, и это соответствие будет правильным.
Таким образом, открывается путь для перспективного подхода к решению задачи установления соответствия, и, помимо этого, возникает еще одна, и весьма привлекательная, возможность. С точки зрения психофизики ?2 G фильтр является монокулярным устройством, а процесс установления соответствия бинокулярен. Это означает, что значения параметров ?2 G-фильтров (например, ширина их рецептивных полей определяются с помощью чисто монокулярных измерений. Диапазон значений диспаратности, в котором развертывается процесс установления соответствий (обычно его называют фузионной зоной Панума; мы будем обозначать его через ?), является понятием сугубо бинокулярным. Если наша теория верна, она должна давать возможность в явном виде прогнозировать новые соотношения между этими априорно не связанными величинами, которые измеряются совершенно различными способами. Следовательно, появляется прекрасный способ проверить нашу теорию.
Итак, требуется вывести точные количественные соотношения, связывающие, как мы полагаем, ширину рецептивного поля wl-D и размеры фузионной зоны Панума ?. Для того чтобы иметь возможность сделать это, нужны некоторая количественная модель каналов, используемых на предварительном этапе обработки зрительной информации, и какой-либо способ оценки возможных интервалов между пересечениями нулевого уровня. Вероятно, следует отметить, что собственно идея почерпнута из нашей предыдущей работы, посвященной первоначальному эскизу. В этой работе большинство клеток, действующих на начальном этапе зрительного пути, рассматриваются не как устройство для обнаружения признаков, а как дифференциальные операторы. Определение Хьюбелом и Уиселом простой кортикальной клетки в качестве линейного устройства привело нас, в частности, к представлению о полосообразном рецептивном поле как о некотором операторе, реализующем вычисление второй производной по определенному направлению, что и составляет основу для последующего нахождения пересечений нулевого уровня. Лишь позже мы осознали, что сами простые клетки, вероятно, и являются устройствами для определения пересечений нулевого уровня. С математической точки зрения эта небольшая путаница не имеет значения, поскольку при очень слабых допущениях обе точки зрения оказываются эквивалентными. С точки же зрения реализации и, следовательно, психофизики это достаточно разные вещи. Позже мы еще вернемся к этой теме.
Итак, проведение нашего анализа требует для фильтров, которые используются в зрительной системе человека, наличия некоторой количественной оценки расстояний, разделяющих пересечения нулевого уровня. В то время когда была сформулирована данная теория стереозрения, основанная на установлении соответствий для различных уровней разрешения, мы еще не знали, что ?2 G-фильтр является оптимальным выбором, но нам уже было известно нечто столь же перспективное, поскольку X. Уилсон только что предложил свою четырехканальную модель структуры каналов. Для их описания он воспользовался РГР — разностью двух гауссовых распределений, которая практически не отличается от ?2 G-фильтра.
Нам также очень повезло в том, что касается математических аспектов задачи, так как получение оценок для возможных расстояний между пересечениями нулевого уровня сигналов с ограниченными спектрами является делом очень трудным. Ряд математиков, начиная с Райса, а позднее Лонге-Хиггинс и Лидбеттер, уже занимались этими вопросами. Задача интересна как таковая, поскольку она возникает в связи с рядом физических явлений, часть которых относится к числу очень важных. Это эффекты броуновского шума, обусловленные случайными перемещениями электронов в электрических цепях (например, некоторые усилители включаются при переходе напряжения через нулевой уровень), а также распределение высоты морских волн, вызывающее сегодня особый интерес из-за того, что человек пытается приступить к использованию этого источника энергии. Кроме того, этот же математический аппарат применяется при изучении бликов на поверхности моря, т. е. тех его участков, от которых солнце отражается как бы прямо в глаза наблюдателю — в результате поверхность моря блестит и сверкает и создается впечатление, что она мерцает.
Итак, существует возможность анализировать пространственные распределения пересечений нулевого уровня, по крайней мере для одномерных сигналов с ограниченным спектром. Результаты такого анализа представлены на рис. 3.17
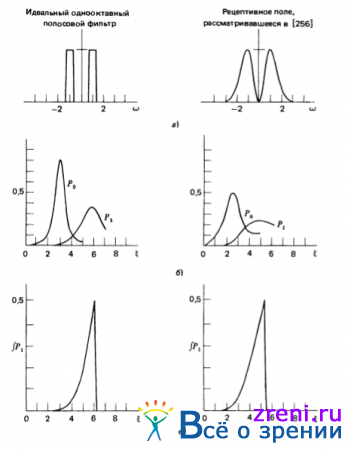
Рис. 3.17. Распределения интервалов разделяющих пересечения нулевого уровня. Фильтрация гауссовского случайного процесса осуществляется с помощью фильтра с определенной амплитудно-частотной характеристикой (а). Приближенные распределения интервалов для первого (Р0) и второго (Р1) пересечений нулевого уровня для гауссовских процессов с нулевыми средними значениями на выходе фильтров (б). Когда пересечение нулевого уровня в начале координат соответствует переходу от отрицательной полуволны сигнала к положительной, вероятность наличия еще одного пересечения нулевого уровня того же знака на расстоянии ? от начала координат приближенно определяется значением интеграла от функции распределения Р1 (в). В левом столбце приведен график для идеального однооктавного фильтра с центральной частотой ? = 2 ?/?, в правом столбце аналогичный график приведен для рецептивного поля. Соотношение пространственных постоянных возбуждения и торможения составляет 1:1,5. Ширина центральной возбуждающей зоны рецептивного поля w равна 2,8 единиц, в которых градуирована ось ?. Для случая, представленного в левом столбце, вероятность ?P1 = 0,001 соответствует интервалу ? - 2,3, а вероятность 0,5 - интервалу ? =6,1. Эти значения для случая, представленного в правом столбце, составляют ? = 1,5 и ? - 5,4. Если соотношение пространственных постоянных составляет 1:1,75, соответствующие значения вероятности ?P1 изменяются не более чем на 5 %
для идеального однооктавного полосового фильтра (левый столбец) — и для ?2G-фильтра, обеспечивающего хорошую аппроксимацию тех фильтров, которые, по мнению Уилсона, действуют на этапах предварительной обработки изображений в зрительной системе человека (правый столбец) — этот случай проиллюстрирован на рис. 3.16.
Необходимые подробности приведены в подписи к рис. 3.17, однако отметим, что особый интерес вызывают два графика, приведенные на рис. 3.17, в. Они указывают вероятность (для случая пересечения нулевого уровня в начале координат) наличия другого пересечения нулевого уровня того же знака на расстоянии ? от начала координат. Масштаб по оси ? для случая, представляющего интерес с биологической точки зрения (справа), соответствует значению ширины рецептивного поля w1-D равному 2,8. Следует обратить внимание на два значения этой вероятности: на расстоянии, равном значению она составляет около 5 %, а на расстоянии, равном значению 2w1-D, она составляет около 50 % и ее значение резко возрастает. Умеренные изменения геометрии фильтра не вызывают существенных изменений значений этой вероятности.
Алгоритм установления соответствий между изображениями стереопары. Опираясь на эти сведения, теперь можно предложить алгоритм установления соответствий между изображениями стереопары и доказать его корректность. Начнем с одного простого случая, когда ложные цели фактически не рассматриваются. Рисунок 3.18, а
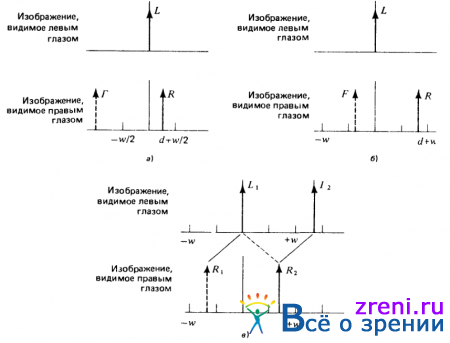
Рис. 3.18. Процесс установления соответствия, ориентированный на левое изображение. Устанавливается соответствие между некоторым пересечением нулевого уровня левого изображения L и пересечением нулевого уровня правого изображения R, смещенным относительно первого на значение диспаратности d. Вероятность появления какой-либо ложной цели относительно пересечения нулевого уровня w в диапазоне значений диспаратности протяженностью R мала, и, следовательно, при d w/2 (а) ложные цели будут почти всегда отсутствовать в диапазоне значений диспаратности протяженностью w/2 Отсюда следует первый из возможных алгоритмов установления соответствий. В противном случае можно рассматривать все соответствия в диапазоне протяженностью w (б) При этом ложные цели, обозначенные на рисунке через F, могут возникать приблизительно в 50 % случаев, однако правильное решение также существует. Если правильное соответствие конвергентно, то ложная цель с высокой вероятностью дивергентна. Итак, при использовании второго алгоритма при однозначности соответствий (для обоих изображений) они принимаются как правильные, а остальные трактуются как неоднозначные и подчиняющиеся эффекту распространения (в). В данном случае можно установить соответствие между L1 и R1, или R 2 и между L2 и R 2. Поскольку оба соответствия имеют одинаковые значения диспаратности, соответствие устанавливается между L 1 и R2
прекрасно иллюстрирует этот случай. Проверяется соответствие некоторого пересечения нулевого уровня левого изображения, обозначенное через L, пересечению нулевого уровня toгo же знака правого изображения, смещенного относительно первого на значение диспаратности d. Правильное соответствие обозначено через R, возможная ложная цель F, ’’притаившаяся” поблизости, изображена штриховой линией. Однако при условии, что рассматривается лишь диапазон значений диспаратности, равный w/2, мы свободны от риска встречи с ложной целью, так как даже если пересечение нулевого уровня R располагается точно на границе диапазона диспаратности (например, d =w/2), проведенный выше статистический анализ гарантирует, что с вероятностью 95 % в диапазоне значений диспаратности, покрывающем ширину w центральной возбуждающей части рецептивного поля, может встретиться лишь одно пересечение нулевого уровня того же знака. Даже если не принимать во внимание все те случаи, когда появляются два кандидата на соответствие, более чем в 95 % случаев нам будет сопутствовать успех.
При этом, конечно, предполагается, что R — правильное соответствие, т. е. оно действительно принадлежит диапазону w/2, изучаемому алгоритмом. Можно, однако, указать, когда правильное соответствие не принадлежит этому диапазону, поскольку, если диспаратность наблюдаемой поверхности входит в этот диапазон, почти для всех пересечений нулевого уровня левого изображения на правом изображении найдутся соответствия и для всех пересечений нулевого уровня левого изображения на правом найдется по меньшей мере один кандидат на соответствие. Если же значение диспаратности такой поверхности выходит за пределы данного диапазона, то вероятность отыскания для некоторого пересечения нулевого уровня левого изображения кандидата на соответствие на правом изображении в пределах указанного диапазона фактически эквивалентна вероятности случайного попадания некоторого пересечения нулевого уровня соответствующего знака правого изображения в определенный пространственный диапазон w/2. Значение этой вероятности составляет около 40 %. Следовательно, если диспаратность поверхности выходит пределы указанного диапазона, будет устанавливаться лишь около 40 % соответствий, против почти 100 %-ного их установления в случае, когда поверхность попадает в соответствующий диапазон диспаратностей. Следовательно, нетрудно указать, когда процесс установления соответствии успешно завершится. Заметим, кстати, что мы опираемся на третье условие нашего основного допущения — непрерывность, поскольку предполагается, что имеется возможность просматривать некоторую окрестность изображения, размеры которой достаточны для эмпирической оценки различия, существующего между случаями 40 %-ной и, скажем, 95 %-ной вероятности установления соответствий. Такая окрестность не должна быть очень большой, но она должна существовать, и именно поэтому нам требуется допущение о непрерывности.
Теперь, после того как с помощью этого простого алгоритма проиллюстрирована основная идея, можно приступить к его усовершенствованию, с тем чтобы расширить диапазон допустимых значений диспаратности от w/2 до w. На рис. 3.18, б изображено уже упоминавшееся пересечение нулевого уровня левого изображения L, однако в данном случае его правильное соответствие на правом изображении R может иметь значение диспаратности d, достигающее значения w. Во-первых, следует отметить, что если диспаратность d принимает положительные значения, то на основании тех же, что и выше, доводов можно по меньшей мере с 95 %-ной вероятностью считать пересечение нулевого уровня R единственным кандидатом на соответствие в диапазоне значений диспаратности от 0 до w. Во-вторых, как показывает проведенный нами статистический анализ, вероятность появления ложной цели в диапазоне значений диспаратности, равном 2 w и включающем значения диспаратности от d = — w до d = w, составляет самое большее 50 %, даже в том случае, когда правильное соответствие находится на одном из концов этого диапазона. Рассматривая эти два обстоятельства в совокупности, мы приходим к выводу, что по меньшей мере в 50 % случаев установление соответствия приводит к получению однозначного и правильного результата, а остальные случаи оказываются неоднозначными и требуют рассмотрения главным образом двух альтернатив — одной конвергентной (в диапазоне (0, w)) и одной дивергентной (в диапазоне (—w, 0)), причем одна из них дает правильное соответствие. Выбор правильной альтернативы в случае неоднозначности может основываться просто на учете знаков соседних соответствий (обратите внимание на использование условия непрерывности). Отметим, кстати, что при проверке соответствия в малой окрестности нулевого значения диспаратности вероятно (р 0,9) наличие лишь единственного кандидата, что снова следует из статистического анализа. Следовательно, представление о трех диапазонах значений диспаратности — конвергентном, дивергентном и расположенном в окрестности нулевого значения - естественно вытекает из данного метода установления соответствий между изображениями стереопары.
Итак, если диспаратность поверхности принадлежит указанному диапазону, почти для 100 % пересечений нулевого уровня будут найдены соответствия; в противном случае эта доля составляет 70 % (вместо 40%, о которых речь шла выше), но она все еще достаточно сильно отличается от 100 %, что позволяет нам указывать, когда процесс установления соответствий успешно завершается.
Добиться существенного расширения допустимого диапазона значений диспаратности w, не прибегая к более мощным методам удаления ложных целей, не удается, поскольку вероятность появления ложных целей довольно резко увеличивается при выходе за пределы диапазона 2w. Например, при сокращении последнего до 1,5 w доля неоднозначных соответствий падает уже до 20%.
Единственность, кооперативностъ и эффект распространения. Э. Гримсон отметил существенную особенность процесса установления соответствия: он может реализовываться при использовании только одного из изображений стереопары либо для обоих изображений одновременно. Так, например, если в случае, представленном на рис. 3.18, в, ориентировать процесс установления соответствий на левое изображение, соответствие для пересечения нулевого уровня L1 неоднозначно, а для пересечения нулевого уровня L 2 — единственно. При ориентации процесса установления соответствий на-правое изображение единственно соответствие для пересечения нулевого уровня R1, но неоднозначно — для R2. Два однозначных соответствия, взятые вместе, составляют правильное решение.
Истинность единственных соответствий, а не неоднозначных следует из условия, единственности, включенного в основное допущение стереопсиса.
Поэтому алгоритм установления соответствий можно организовать таким образом, чтобы он находил и ’’принимал” однозначные соответствия, ориентируясь на каждое из изображений стереопары. Такая конструкция алгоритма, однако, имеет в действительности ряд примечательных следствий, поскольку означает, что условие единственности больше не является проверяемым по определению в алгоритме, в то время как условие непрерывности таковым остается.
Это обстоятельство устанавливается следующим образом. Как мы уже убедились, данный алгоритм предусматривает определение части локальных кандидатов на соответствия, для которых оно фиксируется с тем, чтобы выяснить, принадлежит ли диспаратность наблюдаемой поверхности рассматриваемому диапазону значений диспаратности. Если эта часть близка к 100 % — то все в порядке. Если же нет (в этом случае она, по всей вероятности, составляет 70 %). — полученное решение отвергается. ’’Обмануть” этот тест очень трудно, и, поскольку его обоснование базируется на условии непрерывности, он эквивалентен проверке по определению в алгоритме локального выполнения условия непрерывности на видимых поверхностях.
Иначе обстоят дела с единственностью. Если алгоритм выбирает решения, ориентируясь на их единственность относительно одного из изображений, то это позволяет с его помощью добиваться слияния конфигураций типа граничного случая Панума (рис. 3.19)
Рис. 3.19. Граничная конфигурация, предложенная Панумом. При слиянии возникает впечатление двух прямых, разнесенных по глубине (а). Каждой точке правого изображения ставятся в соответствие две точки левого изображения. При слиянии наблюдатель воспринимает две плоскости. Парные точки не обязательно должны присутствовать лишь на одном из изображений (б). Результаты применения стереоалгоритма к стереограммам на рис. 3.19, б; значения диспаратности представлены таким же образом, как это было сделано на рис. 3.13. На рисунке можно обнаружить две плоскости (в)
не только для изображений с малым числом ’’событий” (типа представленного на рис. 3.19, а), но и для изображений с высокой плотностью заполнения. Для изучения этой проблемы О. Браддик предложил использовать стереограммы, подобные приведенным на рис. 3.19, б: в таких стерео граммах каждой точке правого изображения соответствуют две точки левого. Соответствие, ориентированное на левое изображение, однозначно, поэтому оно принимается, в результате чего возникает перцептивный образ, состоящий из двух плоскостей, которые располагаются одна позади другой. Зрительная система не обладает специфичностью относительно использования правого или левого глаза, и поэтому может случиться, что часть парных объектов окажется на правом изображении, а часть — на левом. Для зрительной системы это безразлично.
По существу, такая ситуация, конечно, невозможна в случае двух реальных поверхностей, и именно поэтому, возможно, мы не предусмотрели в алгоритме внутренней проверки условия единственности. Тем не менее в этой связи возникает одно интересное положение общего характера: некоторые допущения пригодны для внутренней проверки в алгоритме, и такая проверка проводится, некоторые допущения могли бы проверяться таким образом, но не проверяются, например условие единственности; некоторые же допущения вообще невозможно проверить. Ниже мы встретим несколько соответствующих примеров, но сейчас стоит, возможно, отметить, что одним из них может служить иллюзия искаженной комнаты, предложенная Эймсом. В этом случае допущение о том, что углы — прямые, не поддается внутренней проверке без привлечения стереопсиса или какой-либо информации о движении.
И наконец, существуют ситуации, когда соответствие неоднозначно для обоих глаз. При этом неоднозначность можно устранить с помощью информации о знаках соседних соответствий — выбираются соответствия с одинаковыми знаками. Имеется, однако, существенное различие между двумя наиболее очевидными способами осуществления такого выбора. Можно ориентироваться на знаки тех соседних соответствий, которые являлись однозначными с самого начала, но можно и пользоваться знаками тех соседних соответствий, которые к этому моменту установлены. Вторая схема вносит в процедуру механизм кооперации, первая же — нет.
Для того чтобы удостовериться в этом, представим себе стереограмму, синтезированную столь искусно, что все соответствия неоднозначны, за исключением одной области однозначности, расположенной, скажем, на границе. С помощью первой схемы невозможно устранить неоднозначность ни для одного соответствия, относящегося к внутренней части стереограммы, поскольку отсутствует хотя бы одно однозначное соответствие, с которого можно было бы начать. В случае же применения второй схемы процесс снятия неоднозначности будет постепенно распространяться от границ стереограммы, на которых соответствия уже установлены, во внутреннюю часть, в которой в конечном счете будут установлены те соответствия, знаки которых совпадают со знаками соответствий на границах.
Джулес и Чан поставили такой эксперимент. На рис 3.20
Рис. 3.20. Существует много способов установления соответствий в центральной части данной стереограммы, однако обычно воспринимаются лишь те соответствия, диспаратности которых минимальны. Тем не менее некоторое определенное установленное соответствие можно сместить, введя в стереограмму допускающие однозначное установление соответствия точки, обладающие некоторой фиксированной диспаратностью (а). Шесть процентов точек, расположенных в верхней половине квадрата, имеют однозначные соответствия, характеризующиеся перекрестной диспаратностью в две точки (смещение в направлении носа), в нижней же половине квадрата смещение определяется неперекрестной диспаратностью в две точки. Даже при введении смещения на границе обеспечивается возникновение одного из допустимых вариантов слияния в центре (б). Это свидетельствует о том, что алгоритм установления соответствия между изображениями стереопары, действующий в зрительной системе человека, в определенной мере использует кооперативный механизм
приведен пример типа стереограммы, использовавшегося ими. Оказалось, что информация, заключенная в граничной области, может тем или иным способом направлять процесс установления соответствий, обеспечивая его продолжение во внутренние области стереограммы. Из этого следует, что в зрительной системе человека используется вторая из двух указанных выше возможностей
Фузионная зона Панума. Использование второй из описанных выше схем позволяет установить правильные соответствия при диспаратностях, укладывающихся в диапазон, равный w. Точность определения значений диспаратности в этом случае должна быть весьма высокой и составляет некоторую приблизительно постоянную долю значения w (результаты, относящиеся к остроте стереозрения, позволяют оценить ее приблизительно как w/20) Применительно к каналам центральной ямки сетчатки, постулированным в модели Уилсона, это соответствует диспаратности, равной З', и разрешению, равному З'', для канала с минимальным рецептивным полем и, быть может, диспаратности, доходящей до 20', и разрешению, равному 1, для канала с наибольшим рецептивным полем. При эксцентриситете 4° этот диапазон составляет от 5,3'до приблизительно 34'.
При этих допущениях прогнозируемые значения хорошо согласуются с известными результатами измерений порогов слияния, происходящего без использования движений глаз. Митчелл, использовав кратковременную экспозицию раздражителей - коротких отрезков прямых, обнаружил, в полном соответствии с результатами предыдущих исследований, что максимальные значения конвергентной и дивергентной диспаратностей при отсутствии диплопии составляют 10-14' в центральной ямке сетчатки и около 30 - при эксцентриситете в 5°. Таким образом, протяженность так называемой фузионной зоны Панума оказывается вдвое больше этих максимальных значений диспаратности.
Применив в эксперименте стабилизацию сетчаточного изображения, Фендер и Джулес установили, что слияние двух раздражителей-прямых (ширина линии 13', высота 1°) происходит при максимальной диспаратности в 40'. Это значение, вероятно, характеризует полную протяженность фузионной зоны Панума. Воспользовавшись все той же стереограммой, образованной случайными конфигурациями точек, Фендер и Джулес получили значение 14'(6'- смещение и 8'- диспаратность в пределах стереограммы). Поскольку размер точки составлял всего лишь 2', можно предполагать, что на высокочастотные каналы приходится больше энергии, чем на низкочастотные, и, следовательно, нужно ожидать соответственного сужения зоны слияния. Джулес и Чан, используя точки размером 6'при угле наблюдения 5°, без каких-либо затруднений довели значение диспаратности, при которой происходит слияние, до 18'. Принимая во внимание все факторы, можно считать, что эти данные, по-видимому, соответствуют нашим ожиданиям.
Важнейший прогноз, который получен с помощью этой теории, состоит в том, что максимальная диспаратность, при которой слияние еще возможно, должна быть (в определенном смысле) соизмерима с пространственной частотой раздражителя, поскольку нижние пространственные частоты выделяются только с помощью каналов с большими рецептивными полями. Сейчас мы уже располагаем некоторыми свидетельствами о том, что это, возможно, действительно так.
Продолжение в следующей статье: Стереопсис. Часть 3.
----
Статья из книги: Зрение | Д. Марр




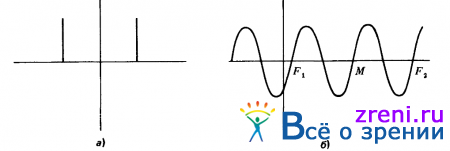


Комментариев 0