Видимое движение | Часть 2

Содержание:
Описание
Критика теории УллманаТеория Уллмана, посвященная процессу установления соответствия, имеет исключительную ценность в качестве первого шага в правильном направлении: после 50 лет путаницы и недоразумений она вносит немного долгожданной и живительной ясности. Ее значение состоит в том, что она позволяет нам формулировать ряд экспериментальных проблем, которые не возникли бы при иных обстоятельствах, и открывает путь рациональному исследованию явления в качестве альтернативы несистематизированной регистрации его феноменологии.
Если оставить на время эмпирические аспекты этой теории, то можно выделить несколько проблем, заслуживающих рассмотрения, особенно в книге, посвященной в первую очередь теории зрительной системы. Первая из них заключается в том, что допущение о независимости, необходимое для использования вероятностного аппарата, не совсем верно в эмпирическом смысле, по крайней мере в простейшей формулировке. В ситуации, представленной на рис. 3.51, а,
Рис. 3.51. На этом рисунке кадр 1 изображен с помощью кружков, а кадр 2 - с помощью крестиков. Наличие элемента С2 не влияет на наличие элемента С1 (а). В случае (б), однако, это влияние существует: пара С1 С2 действует как прямая С - она может перемещаться либо к прямой L, либо к прямой R (в). Если конфигурация (обобщенный признак) разрушается из-за наличия какой-то иной пространственной организации (г), центральная пара элементов больше не рассматривается как прямая С
независимость действительно имеет место: однозначность соответствия С2 — R2 не влияет на неоднозначность поведения С1. В ситуации же, приведенной на рис. 3.51, б, поведение С1 и С2 связано: как указывал Уллман, в сущности, они ведут себя таким образом, как будто служат концевыми точками прямой С, показанной на рис. 3.51, в. Подобное поведение этих элементов не наблюдается при изменении задания способа группировки (рис. 3.51, г).
Итак, создается впечатление, что процесс установления соответствия может в определенных пределах реализовываться не только нэ отдельных элементах, но и на группах, ими образованных. Хотя процесс группировки не связан с получением в явном виде описаний внутренней структуры групп и хотя установление соответствий между группами в целом не является препятствием для установления дополнительных соответствий между их элементами, наличие первых, возможно, ограничивает установление последних. В частности, допускаются те соответствия, которые совместны с соответствиями, установленными для включающей их группы, а несовместные в таком смысле соответствия не допускаются. Внутренняя структура подобного типа может быть представлена в теории с помощью вероятностного аппарата, но выглядит это неуклюже и свидетельствует о том, что мы, вероятно, еще не пришли к наиболее конструктивному подходу.
Перед нами уже возникала вторая проблема: соответствие может устанавливаться между группами без установления соответствий между элементами, их образующими. Сам Уллман отмечал существование такой возможности и в более поздней работе, выполненной совместно с М. Райли, подтвердил и обобщил это наблюдение. Конечно, можно просто включить в теорию Уллмана взаимодействия, подобные этим взаимодействиям элементов высшего уровня (как это предлагает сделать Уллман), однако они не следуют из нее естественно и абсолютно не поддаются прогнозированию с ее помощью. В сущности, они практически противоречат ей, поскольку назначение этой теории в целом — показать, каким образом сложная и порой беспорядочная реализация процесса установления соответствия для различных конфигураций может порождаться сугубо локальными взаимодействиями простых процессоров, отождествляемых с образующими элементами конфигурации.
Что касается третьей проблемы, то ее необходимо рассматривать под несколько иным углом, а именно с позиций человека, создающего теорию. Что, могли бы мы спросить, дает вероятностный подход? И ответ, по существу, сводится к одному — линейность. Практическим следствием в данном случае оказывается то, что сугубо локальные взаимодействия с гарантией обеспечивают достижение как раз искомого глобального минимума. Велика дидактическая ценность этого следствия, поскольку оно показывает, что, как и в случае нашего первого кооперативного стереоалгоритма, искомые глобальные результаты могут достигаться с помощью чисто локальных взаимодействий. С первого взгляда кажется, что именно этого нами следовало бы добиваться, так как известно, что поверхностные связи в коре головного мозга весьма коротки.
Опыт, приобретенный нами при изучении стереопсиса и локально-параллельной организации, заставляет, однако, относиться к этим доводам с осторожностью в связи с теми проблемами, которые возникают из-за итераций. В данном случае нам следует проявлять осторожность потому, что теория Уллмана не имеет статуса некоторого алгоритма — это теория высшего уровня — и, несомненно, существуют неитерационные способы ее реализации. Тем не менее то обстоятельство, что для ее реализации достаточно только локальных взаимодействий, оказывается достоинством лишь в том случае, если она действительно реализуется локально. К сожалению, если исходить из номинальной стоимости этой теории, в которую входит и ее реализация, то, как я полагаю, основным затруднением должно служить то, что скорость сходимости вычислительных процедур такого типа мала (меньше, например, скорости сходимости первого алгоритма стереопсиса). Несомненно, скорость сходимости зависит от начальной точки итерации — и в этом отношении использование приближенной группировки и укрупненных характерных объектов изображения может оказаться полезным, — но даже и в таком случае для получения приемлемого результата может потребоваться от 10 до 70 итераций. Этот довод не столь уж неопровержим: обычно любую проблему, возникающую в связи со скоростью сходимости, удается разрешить с помощью каких-либо специальных ухищрений, тем не менее он ослабляет первоначальную привлекательность теории, построенной на основе концепции простой сети локальных взаимодействий.
Мне значительно труднее сформулировать заключительное замечание, поскольку оно в значительно большей степени, чем остальные, основывается на неподтвержденных интуитивных представлениях о работе мозга. В основном, как я считаю, они сводятся к тому, что на этих достаточно низких уровнях вероятностные подходы (такие как принцип максимального правдоподобия) не используются. Частично это интуитивное убеждение возникло у меня в результате неоднократных попыток воспользоваться вероятностными методами. Применение вероятностного подхода в задаче стереопсиса дает нечто напоминающее корреляцию уровней серого тона, и я однажды предпринял попытку привлечь этот подход для решения некоторых задач, связанных с 2,5-мерным эскизом; частично это интуитивное убеждение явилось следствием общего представления о недостаточной определенности (в некотором смысле) вероятностного подхода. Решение задачи любой сложности, полученное методом максимального правдоподобия, всегда в значительней степени неправдоподобно (в техническом смысле). Тем не менее ответы, предлагаемые зрительной системой, почти всегда правильны и, более того, обычно сопровождаются субъективным ощущением определенности (изредка — сомнением). Эти ответы значительно определеннее и значительно чаще оказываются правильными по сравнению с теми, которые соответствовали бы достаточно низкому значению вероятности. В аналогичных ситуациях я обычно обнаруживал, что для описания устройства реального мира имеются лучшие ограничения и часто именно они позволяют обеспечивать значительно более прочную основу для информационной теории.
Другими словами, если бы мне пришлось отвечать на вопрос, сформулированный в конце раздела, посвященного стереопсису: правильно ли выбрана задача, которая является предметом информационной теории? — я бы ответил более уклончиво, чем если бы речь шла о стереопсисе или второй части теории Уллмана, посвященной задаче определения структуры по движению. Я до сих пор не располагаю какой-либо определенной альтернативой, однако нижеследующие замечания указывают перспективу, в которой эта проблема мне видится.
Новый взгляд на задачу установления соответствия
Одна или две задачи? Сердцевиной всякой информационной теории зрительного процесса является ответ на следующий вопрос: для чего данный процесс предназначен? В модели Уллмана целью процесса установления соответствий является определение некоторой связи между последовательно поступающими кадрами, что позволяет выявлять изменения, происходящие при смене кадров. Регистрация этих изменений дает возможность затем задать входную информацию для процессов, обеспечивающих восстановление структур и их движения.
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
Не вызывает сомнения то, что это составляет по меньшей мере часть тех задач, для выполнения которых предназначен процесс установления соответствий, но исчерпывается ли этим его роль? Забегая немного вперед, можно заметить, что восстановление структуры по движению предполагает (внутренне проверяемым образом) введение допущения о жесткости движущихся тел. Следовательно, задачу установления соответствий можно в первую очередь анализировать с точки зрения некоторого наблюдателя, помещенного в среду с жесткими движущимися телами.
При небольших временных интервалах задача установления соответствий, возникающая в такой ситуации, фактически эквивалентна задаче установления соответствия, возникающей в стереопсисе, поскольку небольшие смещение и поворот некоторого объекта вызывают такой же эффект, как и небольшие смещение и поворот одного из глаз. Конечно, различные тела могут по-разному двигаться, порождая эквивалентность относительно различных пар положений глаз. Однако теория соответствия при стереопсисе имеет локальный характер и может применяться локально при условии, что введенные в ней допущения выполняются локально. Допущения эти состоят в том, что поверхности обладают локальной гладкостью, а соответствия являются однозначными, поскольку любая выбранная позиция всегда переходит только в какую-то другую единственную позицию, а это почти всегда означает ее наличие на данном изображении. Некоторые видимые точки, естественно, переходят в невидимые, и наоборот, но это аналогично тому, что при изменениях стереоскопической глубины один глаз может видеть части поверхности, которые невидимы для другого глаза.
Как же тогда быть с явлениями расщепления и слияния при видимом движении, когда один элемент кадра при переходе к следующему кадру расщепляется, вступая в соответствие с двумя элементами последнего (или наоборот)? Эти широко известные явления, отчетливо проявляющиеся в видимом движении, порождают значительные теоретические проблемы. Насколько часто они должны были бы возникать в контексте восстановления структуры по движению? Мы уже убедились в том, что они могут возникать при стереопсисе - как на физическом уровне (в тех редких случаях, когда оказывается, что два характерных элемента поверхности, различимые одним глазом, относительно другого глаза расположены на линии прямой видимости), так и на психофизическом, что соответствует граничному случаю Панума. Изучив стереограммы Браддика, мы установили даже, что зрительная система человека очень терпимо относится к двойным соответствиям при условии, что для одного из глаз они являются единственными. В этих случаях, однако, причины их возникновения не относятся к разряду фундаментальных; они должны быть связаны с реализацией и возникают главным образом из-за того, что условие единственности обеспечивается в реальном мире в столь сильной степени, что зрительная система может позволить себе считать их выполненными без внутренней проверки.
Относятся ли явления расщепления и слияния при видимом движении к той же категории, что и аналогичные явления, возникающие при решении задачи установления соответствия между изображениями стереопары, или они имеют более фундаментальный характер? Я полагаю, что, приняв точку зрения, согласно которой единственной функцией процесса установления соответствия при движении является решение задач, возникающих в связи с движением твердых тел, последние можно решить точно таким же способом, как и эквивалентную задачу установления соответствия между изображениями стереопары. Эти явления должны получить почти такие же объяснения, как это было сделано для примеров граничного случая Панума при стереопсисе.
Такой подход, однако, не вполне удовлетворителен. Одной, хотя и довольно субъективной, причиной для такого заключения служит то, что разновидность стереопсиса, которая достигается при непосредственном сопоставлении яркостных переходов текстуры, имеет столь состязательный характер, а создающееся в этом случае впечатление глубины столь незначительно, что возникает ощущение отсутствия "подлинного” стереопсиса — присутствуют лишь неявные предварительные намеки на него (скажем, управление вергентными движениями глаз). В видимом же движении эти впечатления вовсе не смутны: яркостные переходы такого рода отчетливо различаются при движении. Соответствия, устанавливаемые в парах, даже столь несходных, как, вполне отчетливы и определенны, а состязательность, как это имеет место в стереопсисе, полностью исключена.
Другой довод, который кажется мне неотразимым, следует из сообщения о возможности возникновения видимого движения между субъективными контурами и даже между диспаратными яркостными переходами в стереограмме, образованной случайными точками. С нашей узкой точки зрения это чуть ли не парадокс, поскольку после того, как диспаратные яркостные переходы найдены, мы имеем дело уже с трехмерной структурой и, следовательно, зачем тогда вообще нужно затевать весь этот процесс восстановления структуры по движению, обеспечивающий получение трехмерной структуры?
Очевидно, как мне кажется, наша узкая точка зрения неадекватна — просто невозможно допустить, чтобы процесс установления соответствий при движении имел столь ограниченный характер. В чем же тогда состоят его принципиальные отличия от процесса установления соответствия между изображениями стереопары?
Решающее различие состоит в том, что один из них развивается в пространстве, а другой — во времени. Для твердых тел эти процессы эквивалентны, но для пластичных поверхностей — нет. Очертания некоторого объекта при восприятии его левым глазом всегда совпадают с его очертаниями, воспринимаемыми в тот же момент времени правым глазом, но мгновения спустя эти очертания могут измениться, и бывает это вовсе не так уж редко. Птица при наблюдении издалека, например, очень быстро меняет свои очертания и облик как из-за того, что она не является твердым телом, так и, вероятно, из-за того, что лучи солнца падают на ее поднимающиеся и опускающиеся крылья под одним и тем же определенным углом. Изображение птицы может быть очень небольшим и с трудом поддающимся разбиению на более или менее твердые компоненты. Тем не менее, хотя из ее движений можно извлечь очень мало или вообще не извлечь никаких данных, непосредственно характеризующих ее структуру, не возникает сомнений в том, что, несмотря на все наблюдаемые изменения внешнего облика, речь все время идет об одной и той же птице. Другими словами, время вносит важный новый фактор, который достаточно независим от деталей трехмерной структуры объекта. Этим фактором является сохранение объектом ’’индивидуальности” во времени, и это составляет совершенно другую задачу. Для того чтобы показать разницу, рассмотрим просто пример Уллмана — ’’лягушка, превращающаяся в принцессу”. Этот пример не относится к задаче восстановления структуры по движению, поскольку структура здесь изменяется, но он относится к проблеме индивидуальности объекта.
Я считаю, что теория должна трактовать эти две задачи независимо, так как порождаемые ими требования к обработке информации несколько различны. Идея установления соответствия между яркостными переходами абсолютно непонятна с точки зрения первого подхода, но совершенно естественна и чуть ли не без тени всяких сомнений привлекательна с точки зрения второго. Обратимся, например, к конфигурациям, порождаемым игрой света на речной поверхности. Все постоянные факторы в данном случае отражают исключительно геометрию русла реки, и, следовательно, именно ее и следует принимать во внимание независимо от сияния речной поверхности. Такая ситуация вполне может служить реальным прототипом ’’регистрограмм движения” случайных точек, использовавшихся Б. Джулесом; вполне понятно, что мы должны быть в состоянии воспринимать такие ’’регистрограммы движения”. Если на рыбе, неторопливо скользящей по поверхности реки, имеется непрерывно меняющийся узор, образованный светом и тенью, то обнаружить ее можно только по ее диспаратным границам. Указанные границы перемещаются, но рыба все время остается одной и той же. Эта проблема относится к сохранению индивидуальности объекта.
Отдельные системы для структуры и сохранения индивидуальности объекта. Итак, проблемы, порождаемые временным фактором, определяют по меньшей мере две различные задачи для процесса установления соответствий при видимом движении, причем сами эти задачи отличаются от первой из двух у Браддика. Первая задача представляет собой первую половину проблемы восстановления структуры по движению, и для случая движения твердых тел она фактически эквивалентна задаче установления соответствия при стереопсисе. Единственная разница между ними заключается в том, что в случае движения добавляется небольшой поворот одного из изображений, но новых существенных проблем это не вызывает. Цель, как и в стереопсисе, состоит в достижении очень детализированного соответствия точно локализуемых объектов на изображении, с тем чтобы измерение изменений их положений на изображении могло выполняться с точностью (второго порядка), необходимой для обработки информации, обеспечивающей восстановление структуры по движению. Следует ожидать, что достижение такой точности предполагает в данном случае использование непроизводных элементов, относящихся к достаточно низкому уровню и подобных входящим в необработанный первоначальный эскиз, либо, быть может, даже просто пересечений нулевого уровня.
Иными являются цели во второй задаче, и определяются они именно тем, что некоторый объект в процессе наблюдения во времени может измениться, что не может иметь место при изменении позиции наблюдателя в пространстве: он может изменить и свои очертания, и конфигурацию (и даже отражательную способность). Точность не является здесь целью — она заключается в приблизительном сохранении индивидуальности объекта — в этом и состоит ключ к пониманию разницы между наблюдаемым движением и стереопсисом. Установление приближенного соответствия между изображениями стереопары не является самоцелью — оно имеет смысл лишь как прелюдия к установлению точного соответствия. Таким образом, приближенные соответствия оказываются лишь неясными и конкурирующими продуктами восприятия. Однако существенное значению имеет установление приближенного соответствия во времени, поскольку оно открывает возможности для обеспечения непрерывности объекта.
Итак, как я полагаю, в этой ситуации может потребоваться создание двух теорий: для случая, когда рассматриваемый объект изменяется и перемещается, и для случая, когда он только перемещается. В первой должно использоваться все то, что только может использоваться, в том числе непроизводные элементы высшего уровня в сочетании с нежесткими правилами установления соответствий и вся доступная трехмерная информация. Явления, связанные с субъективно плавными движениями, могут даже в большей степени оказаться предметом первой, а не второй теории, так как при восприятии плавность ’’идет рука об руку” с сохранением индивидуальности объекта, а из работы Аттнива нам известно, что плавность сопряжена с воспринимаемыми расстояниями в трехмерном пространстве. Вторая теория относится к более низкому уровню, эквивалентному в информационном смысле стерео-псису. И хотя реализация может быть иной, в этой связи имеет смысл подумать о пересечениях нулевого уровня.
↑ Восстановление структуры по движению
Задача
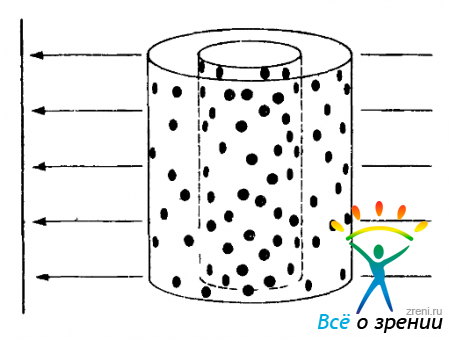
Мы уже убедились благодаря эксперименту Уллмана с цилиндрами, поворачивающимися в противоположных направлениях (рис. 3.52),
Рис. 3.52. Иллюстрация эксперимента Уллмана с цилиндрами, поворачивающимися в противоположных направлениях. Точки, нанесенные на оба цилиндра, как показано стрелками, ортографически проектируются на экран, порождая в результате некоторую последовательность кадров, аналогичных приведенным на рис. 3.53. Каждый отдельный кадр представляет собой некоторое множество случайных точек, однако при предъявлении последовательности таких кадров в динамике становятся отчетливо видны поворачивающиеся цилиндры
что и разбиение сцены на отдельные объекты, и восстановление их очертаний в трехмерном пространстве могут быть обеспечены в том случае, когда единственно доступной информацией является та, которую удается почерпнуть из вида объектов, меняющегося по мере их движения. Каждый кадр, используемый в этом эксперименте, включает внешне случайную совокупность точек и сам по себе интерпретации не поддается. Только при предъявлении таких кадров в виде некоторой непрерывной последовательности движение точек обеспечивает восприятие двух цилиндров, поворачивающихся в противоположных направлениях.
Следовательно, мы будем рассматривать упрощенную задачу интерпретации последовательности кадров, каждый из которых образован некоторым множеством случайных точек. В реальных условиях кадры содержат более сложные, чем точки, непроизводные элементы, однако, как и в случае стереопсиса, это простое представление позволяет отражать сущность задачи. Более того, будем предполагать, что с помощью процесса установления соответствий, рассмотренного выше, соответствие между последовательными кадрами уже установлено. Фактически нам потребуется лишь простая разновидность процесса установления соответствий, а именно процесс, ориентированный на твердые объекты, который, как нам теперь известно, с информационной точки зрения эквивалентен процессу, обеспечивающему решение задачи установления соответствия при стереопсисе.
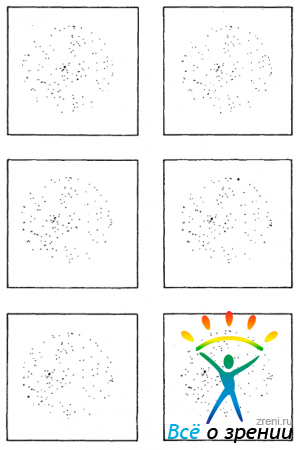
Итак, наша очередная задача характеризуется некоторым набором данных, аналогичным представленным на рис. 3.53.
Рис. 3.53. Задача восстановления структуры по движению. В приведенном наборе кадров содержится трехмерная информация (см. рис. 3.52). Каким образом следует ее восстанавливать?
Каждый кадр образован множеством помеченных точек (хотя метки на рисунке не показаны), причем точка А кадра 1 соответствует точке А кадра 2 и т. д. Вопрос состоит в следующем: как осмыслить эти данные? Каким образом следует действовать, с тем чтобы найти для них разумную трехмерную интерпретацию9
В данном случае возникает точно такое же затруднение, с которым мы уже сталкивались в задаче стереопсиса, а именно решение не полностью определено. Существует бесконечное число трехмерных конфигураций, способных посредством прямоугольной проекции порождать изображения, приведенные на рис. 3.53, скажем произвольное число различных и случайным образом изменяющихся снежных вихрей. Мы не видим, однако, эти различные возможные варианты, мы видим только один вариант, и именно он является правильным.
Поэтому точно так же, как и в стереопсисе, мы должны использовать дополнительную для задачи информацию, с тем чтобы ввести ограничения на искомое решение. Она должна быть одновременно содержательной, истинной и в достаточной мере универсальной. Содержательность определяется тем, что такая информация определяет обычно единственное решение: истинность следует не только из того, что человек в действительности воспринимает лишь одно решение, но и из того, что это решение является также правильным и с точки зрения реальностей внешнего мира; универсальность же требуется потому, что данная система имеет дело с новыми ситуациями, не располагая конкретными априорными сведениями об очертаниях наблюдаемых объектов.
Известный подход
Хотя известен ряд подходов к решению рассматриваемой задачи, лишь один из них заслуживает комментариев. Он был предложен Гельмгольцем, который ввел в обращение идею об аналогичности движения и стереопсиса, в частности об аналогичности восстановления структуры по движению и восстановления расстояния по диспаратности.
Эта идея, однако, имела серьезный недостаток из-за того, что различные объекты, находящиеся в различных частях зрительного поля, могут участвовать в совершенно различных движениях. В данном случае для задачи установления соответствий это несущественно, поскольку процесс установления соответствий имеет сугубо локальный характер. Мы уже использовали то обстоятельство, что для случая твердых объектов и коротких временных интервалов обе задачи установления соответствий, в сущности, эквивалентны. Отмечалось, однако (не испытав по этому поводу особого беспокойства), что
два различных локальных перемещения должны порождать две различные позиции пар глаз, с тем чтобы возникала эквивалентность задаче установления соответствия между изображениями стереопары. Причина, по которой это не вызвало у нас беспокойства, состоит в том, что при установлении соответствия правила объединения не зависят от точных позиций глаз. Эти позиции должны быть лишь близки друг к другу, обеспечивая таким образом аналогичный обзор. Следовательно, на установление соответствия не влияет тот факт, что различные части поля зрения практически порождают различные эквивалентные позиции пар глаз.
Иначе, однако, обстоит дело с восстановлением глубины по диспаратности. Как мы убедились, этот процесс решающим образом зависит от эффективного глазного базиса 5, причем, вообще говоря, порождаемые значения ? различны для каждого твердого объекта, движущегося по ’’индивидуальной программе”. Отсутствует способ определения этих значений априори, и, поскольку они изменяются, невозможно сравнивать происходящее в одной из частей поля зрения с происходящим в какой-то другой его части. Следовательно, несмотря на адекватность использования этого подхода для решения задач установления соответствия в двух указанных случаях (при условии, что один из них ограничивается движением твердых тел и короткими временными промежутками), он совершенно не годится для восстановления трехмерной структуры.
Из этих замечаний следует, что изменения скорости перемещения в поле зрения (которые аналогичны изменениям диспаратности) не должны непосредственно порождать впечатление глубины, а равенство скоростей также не обязательно должно служить очень полезным средством группировки. В гештальтпсихологии, например, известно понятие ’’группировки по принципу общей судьбы”, предусматривающее группировку на основании одинаковых скоростей; Поттер недавно снова обратился к одному из вариантов этой идеи. В демонстрационном эксперименте с цилиндрами, вращающимися в противоположных направлениях, возникают, однако, точки, имеющие одинаковые скорости, но расположенные на разных цилиндрах. Свидетельство, противоречащее другой части утверждения и указывающее, что изменения скорости должны порождать изменения в восприятии глубины, предоставляется демонстрационным экспериментом Уллмана с лентой конвейера, который иллюстрируется на рис. 3.54.
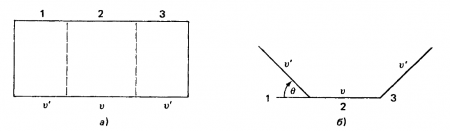
Рис. 3.54. Демонстрационный эксперимент с лен гой конвейера. Точки, расположенные в зонах 1 и 2, перемещаются вправо со скоростью v'=v cos ? , а точки, расположенные в зоне 2, - со скоростью v. Наблюдатель, видящий изображение, приведенное на рис.3.54, а, не воспринимает геометрическую конфигурацию, приведенную на рис. 3.54, б. Вместо этого создается впечатление, что все зоны расположены во фронтальной плоскости, а точки, лежащие в зоне 2, движутся быстрее
Скорость точек, расположенных в зонах 1 и 3, равна и, а точек, расположенных в зоне 2, равна v. Наблюдатель не воспринимает различные участки ленты как плоскости, лежащие на различной глубине, или даже как конфигурацию, приведенную на рис. 3.54, б. Вместо этого все точки воспринимаются на одной и той же фронтальной плоскости; возникает впечатление, что при переходе из зоны 1 в зону 2 их скорость увеличивается, а при переходе из зоны 2 в зону 3 - уменьшается.
Ограничение, предполагающее жесткость тела
Большинство структур видимого мира являются жесткими или по меньшей мере почти таковыми. Многие из изучавших восприятие движения обращали на это внимание (например, Уоллак и О’Коннелл, Гибсон и Гибсон, Грин, Хей, Йоханссон), и в результате возникло убеждение, что жесткость играет в этой задаче особую роль. Им не удалось осознать того, на что указал Уллман: поиск ’’жестких” интерпретаций — это не просто прихоть нашего механизма восприятия движения, он дает возможность человеку однозначно решать задачу восстановления структуры по движению, не прибегая к использованию каких бы то ни было дополнительных ограничений. Этот поразительный факт следует из одного математического результата, названного Уллманом теоремой об определении структуры по движению. Она утверждает, что при задании трех различных прямоугольных проекций четырех некомпланарных точек, принадлежащих некоторой жесткой конфигурации, структуры и движения, совместные с тремя заданными проекциями, определяются однозначно с точностью до отражения, при котором ближайшие точки становятся наиболее удаленными. Другими словами, трех проекций четырех некомпланарных точек достаточно для определения их трехмерной структуры при условии, что задача установления соответствий уже решена. Кроме того, справедливость этого результата не ограничивается случаем видимого движения: для непрерывного движения исключительно от разрешающей способности систем, измеряющих временные изменения позиций объекта, зависит, что именно рассматривается в качестве соответствующих трех проекций.
Комбинация ’’четыре точки — три проекции” в теореме о восстановлении структуры по движению является минимальной в следующем смысле. Если проекций только две, то можно построить произвольное количество точек, не имеющих единственной трехмерной интерпретации (хотя отдельные комбинации, к счастью, будут ее допускать). Таким образом, в общем случае двух кадров недостаточно. В случае трех кадров трех точек снова, вообще говоря, оказывается слишком мало для получения однозначного решения — требуются четыре точки.
Для четырех точек и трех проекций можно предложить достаточно правдоподобное доказательство, основанное на понятии числа степеней свободы, соответствующих этому случаю. Пусть указанные четыре точки обозначены как О, А, В и С, причем точка О всегда представляет начало координат (0,0,0), а три проекции — как 1, 2 и 3. Необходимо определить 15 переменных. Девять из них задают для проекции 1 положения, занимаемые в трехмерном пространстве точками А, В и С относительно точки О (три точки с тремя координатами для каждой из них); остальные шесть переменных задают повороты в трехмерном пространстве, необходимые для получения проекций 2 и 3 из проекции 1. (Мы исключаем переносы, совмещая на всех проекциях точки О.) Для определения поворота а трехмерном пространстве требуются три переменные, для определения оси - две переменные, а для определения величины поворота нужна одна переменная.
Всю информацию, которую мы получаем из каждой проекции, составляют 6 отношений — двухмерные координаты для каждой из точек А, В и С. (Точка О всегда имеет координаты [0, 0].) Следовательно, две проекции дают нам 12 отношений, что недостаточно для определения структуры, поскольку число неизвестных равно 15. Три проекции дают 18 отношений, т.е. их количество больше 15, и этого достаточно при условии, что особых точек или внутренних зависимостей не слишком много. Трудная часть доказательства связана с установлением того, что эти 18 отношений действительно независимы. То обстоятельство, что имеется 18 отношений, а неизвестных всего 15, свидетельствует о том, что часть информации не используется, и именно это в конечном счете обеспечивает возможность внутренней проверки гипотезы о жесткости объектов наблюдения.
Допущение, предполагающее жесткость объектов наблюдения
Проанализировав использование избирательности по направлению для определения свойств видимых поверхностей, мы обнаружили, что линии, характеризующие нарушение непрерывности по направлению движения, случайно не возникают. Они должны свидетельствовать о существовании границы, разделяющей поверхности, движение которых несовместно. Рассмотрев проблему стереопсиса, мы установили, что условия единственности и непрерывности гарантируют существование и единственность решения; соответствующая теорема составила основу для анализа стереозрения, поскольку она позволила сформулировать и использовать в дальнейшем фундаментальное допущение стереопсиса.
То же самое справедливо и в данном случае. Теорема о восстановлении структуры по движению в сочетании с прописной истиной, что большая часть объектов реального мира обладает локальной жесткостью, позволяет нам сформулировать основное допущение для восстановления структуры по движению. Оно было определено Уллманом как допущение о жесткости объектов наблюдения и сформулировано следующим образом: любая совокупность элементов, подвергающихся некоторому двухмерному преобразованию и допускающая единственную интерпретацию в виде некоторого твердого тела, движущегося в пространстве, порождается таким движущимся твердым телом и, следовательно, должна интерпретироваться как таковое.
Из теоремы о восстановлении структуры по движению следует, что в случае твердого тела его трехмерную структуру можно определить по трем кадрам (с точностью до симметрии, поскольку мы работаем с прямоугольной проекцией). Если жесткость отсутствует, вероятность получения случайной жесткой интерпретации пренебрежимо мала, так что на практике этот метод не приведет к успеху. Он, следовательно, обеспечивает самоконтроль (’’внутреннюю проверку”) : если мы в состоянии восстановить трехмерную структуру, которая согласуется с имеющимися данными, то можно считать, что она единственна и верна. Теорема о восстановлении структуры по движению доказывается конструктивно, что дает возможность записать некоторую систему уравнений, решение которой, если оно существует, определяет искомую трехмерную структуру.
Реализация такой схемы решения не вызывает затруднений, так как при этом требуется в качестве исходных данных задать лишь четыре точки и поэтому решение может осуществляться параллельно и независимо на всем зрительном поле. Это обстоятельство делает данную схему решения особенно привлекательной при объяснении того, каким образом человек воспринимает движение. Тем не менее конкретные алгоритмы, возникающие в результате непосредственного применения методов, используемых при доказательстве теоремы, неправдоподобны в биологическом отношении. Они, в частности, не отвечают всем тем принципам, скажем принципу пристойного ухудшения. Если просто записать необходимые уравнения и решить их, то это приведет к алгоритму, который окажется чересчур грубым. Если данные неточны либо наблюдаемый объект недостаточно жесткий, то этот метод ’’работать” не будет и пользоваться им бесполезно.
На самом деле требуется некоторый алгоритм, характеризующийся пристойным ухудшением, по меньшей мере в двух смыслах. Во-первых, если исходные данные искажены шумом, но имеются более чем три проекции, искомый алгоритм должен обеспечить сначала получение приближенного описания структуры, которое, однако, становится почти точным по мере предъявления алгоритму большего числа проекций и увеличения объема сообщаемой ему информации. И, во-вторых, если наблюдаемые объекты не вполне жесткие, искомый алгоритм должен обеспечить получение не вполне жесткой структуры, возможно, снова за счет использования им большего числа точек или проекций. Алгоритмы, обладающие робастностью такого типа, разрабатываются в нашей лаборатории.
До тех пор пока некоторый конкретный алгоритм не предложен в качестве кандидата на роль алгоритма, который действительно используется зрительной системой человека, и пока не проведены соответствующие психофизические и нейрофизиологические эксперименты, мы не будем наверняка знать, адекватен ли данный подход к восприятию движения. Одна вещь, однако, совершенно ясна: теперь нам известно, какие экспериментальные задачи актуальны. До тех пор пока Уллман не обратился к информационному подходу для решения этой задачи, мы этого не знали.
Замечание о центральной проекции
Считается, что алгоритмы, предназначенные для расшифровки не прямоугольных, а центральных проекций не входят в арсенал зрительной системы человека. Причина этого, вероятно, состоит в том, что изменения, соответствующие переходу от одного кадра к следующему, обычно малы уже сами по себе, а разница в изменениях, наблюдаемых на проекциях этих двух типов, обычно действительно очень мала. Психофизические данные указывают, что движение в направлении от наблюдателя, которое порождает изменения лишь в центральной, но не в прямоугольной проекции, не обеспечивает столь же четкого восприятия трехмерной структуры, как для движений других типов. Схема восстановления структуры по движению является, однако, локальной по существу, поскольку ее рабочие ’’ядра” состоят всего из четырех точек. Даже центральная проекция является локально прямоугольной, и поэтому практически не возникает затруднений при использовании ортографических методов восстановления по проекциям, аналогичных схеме Уллмана, даже в тех случаях, когда реальное изображение представляет собой перспективу.
↑ Оптический поток
Дж. Гибсон продолжительное время считал, что ’’основным в зрительном восприятии является способ восприятия поверхностей. Соответствующий образ всегда содержит как субъективный, так и объективный компонент, т. е. он определяет положение наблюдателя, его перемещения и их направления, а также расположение, наклони очертания поверхности”. Шестнадцать лет спустя он высказал аналогичную точку зрения, проиллюстрировав ее рис. 3.55.
Рис. 3.55. Пример оптического потока, порождаемого движением, предложенный Гибсоном. Стрелки представляют значения угловой скорости, которые равны нулю непосредственно впереди и сзади
Очень скоро началось изучение математических аспектов этой гипотезы, но затрагивались лишь отдельные частные случаи либо частные особенности общего случая. Накаяма и Лумис показали, каким образом контуры глубины могут извлекаться из представления на сетчатке поля вектора скорости, порожденного движением наблюдателя. Только недавно, однако, удалось прийти к общей трактовке этой проблемы.
Задача об оптическом потоке, а мы будем пользоваться именно последним термином, заключается в использовании поля вектора скорости на сетчатке, порожденного движением наблюдателя, для определения трехмерной структуры видимых наблюдателю поверхностей. Предполагается, что эти видимые поверхности неподвижны. Принципиальное отличие данного подхода от подхода Уллмана заключается в том, что эффекты, связанные с оптическим потоком основываются на использовании нормальной проекции, а подход, предусматривающий восстановление структуры по движению, является принципиально ортографическим. Таким образом, метод оптического потока позволяет, вообще говоря, работать с плоскими поверхностями, т. е. когда подход, предусматривающий восстановление структуры по движению, неизбежно терпит неудачу.
Исходное представление
Ту информацию, которую называют оптическим потоком и на использовании которой основывается наш анализ, можно рассматривать как мгновенное поле вектора позиционной скорости, ставящее в соответствие каждому элементу на сетчатке мгновенное значение этого элемента. Обычно считается, что элементы имеют некоторую физическую интерпретацию.
Получать эту информацию отнюдь не так просто, как порой предполагают приверженцы метода оптического потока. Мы уже убедились в том, что из-за существования проблемы апертуры локальные измерения как таковые мало что могут дать, кроме направления движения. Фактически полное определение оптического потока эквивалентно решению более простой из двух задач установления соответствия в случае видимого движения, поскольку знание поля скоростей ’’течения” позволяет устанавливать соответствия между двумя кадрами, снятыми с очень небольшими временными интервалами. Следовательно, если зрительная система человека анализирует оптический поток, то при этом в качестве исходных должны использоваться такие же данные, что и при определении структуры по движению.
Математические результаты
Если наблюдатель приближается к некоторой неподвижной поверхности по прямой, то точке их встречи соответствует особая точка поля оптического потока и время встречи определяется исключительно угловыми скоростями поля. Сомнительно, что эти положения существенно используются в зрительной системе человека, поскольку Джонстон, Уайт и Камминг, смоделировав оптическое расширение, возникающее при приближении к поверхности, показали, что человек в состоянии надежно определить фокальную точку расширения лишь непосредственно перед кажущимся контактом с поверхностью. Обучая ученика посадке самолета, летчик-инструктор тратит некоторое время на объяснение того, что текущей расчетной точкой приземления является фокальная точка расширения. Приобретение такого навыка требует сосредоточенности и тренировки, поскольку в его основе не лежит какой-либо естественный рефлекс. Таким образом, гипотеза Гибсона о важности роли, выполняемой фокальной точкой оптического расширения при управлении локомоциями, вероятно, ошибочна применительно к человеку, хотя, быть может, более уместна применительно к птицам.
Авторитетное изложение математических аспектов метода оптического потока появилось сравнительно недавно. Было показано, что вообще по монокулярной проекции жесткой текстурированной кривой поверхности можно определить ее градиент в любой точке, по полю вектора скорости изменяющегося на сетчатке — перемещения глаза относительно этой поверхности, а также первую и вторую производные поля. Соответствующая система уравнений избыточна, что обеспечивает возможность проверки допущения о жесткости.
Существует интересное различие между этим результатом и теоремой Уллмана о восстановлении структуры по движению. Согласно схеме Уллмана четыре точки составляют достаточную информацию при условии, что наблюдатель ждет столько, сколько необходимо для получения по меньшей мере трех различных проекций этих точек. В схеме Лонге—Хиггинза и Праздни достигается иной компромисс: требуются лишь два кадра и поэтому время, затрачиваемое на проведение измерений, оказывается меньшим. (В данном случае достаточно двух кадров, поскольку восстановление очертаний основывается на использовании центральной, а не прямоугольной проекции.) С другой стороны, локальные пространственные окрестности, используемые в процессе решения, это не просто точки, как в схеме Уллмана: их размеры должны быть достаточными для того, чтобы обеспечивалось получение надежных оценок первой и второй пространственных производных поля вектора скорости.
Этот анализ являет собой еще один пример того, каким образом информационная теория может содействовать экспериментальным исследованиям. Проведя математический анализ этой задачи (а он, несомненно, намного запоздал), Лонге—Хиггинз и Праздни создали теоретическую схему для исследования того, действительно ли мы, люди, используем оптический поток, как предположил Гибсон, и если это так, то каким образом. Уже ясно, что существует ряд способов использования оптического потока, которые мы реально не используем. Еще одним примером служит демонстрационный эксперимент Уллмана с лентой конвейера, который иллюстрируется рис. 3.54. Мы не воспринимаем зрительно, что геометрия зон 1 и 3 отличается от геометрии зоны 2, в то время как большинство теорий оптического потока будет настаивать на том, что мы должны видеть это отличие.
Мы тем не менее все же могли бы в какой-то форме использовать оптический поток, возможно лишь в незначительной степени и в основном в периферическом, а не центральном зрении. Таким образом, в конечном счете в тех случаях, когда можно предположить точность измерений малой для системы, основанной на схеме Уллмана восстановления структуры по движению, следует также рассчитывать обнаружить наиболее очевидные проявления оптического потока. Остается установить, используется ли оптический поток в зрении человека.
----
Статья из книги: Зрение | Д. Марр


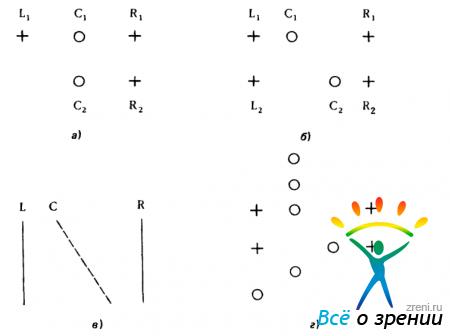
Комментариев 0