Психофизиология цветового зрения | Модель Харвича и Джемсон

Описание
В историческом экскурсе в начале книги мы рассматривали причины отвержения одностадийной концепции и замены ее двухстадийной. И хотя первые идеи о втором звене цветового анализатора появились еще в начале нашего века, реально, в качестве сформировавшейся теории, двухстадийная концепция появляется только в 50-е годы.Первую математическую модель, основанную на широком круге экспериментальных измерений, предложили американские исследователи Харвич и Джемсон.
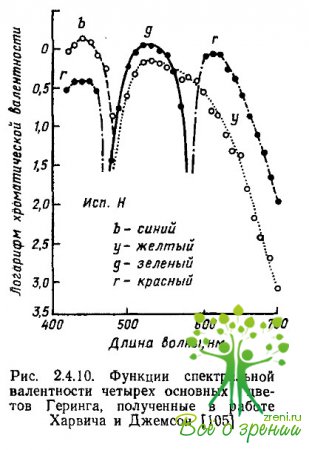
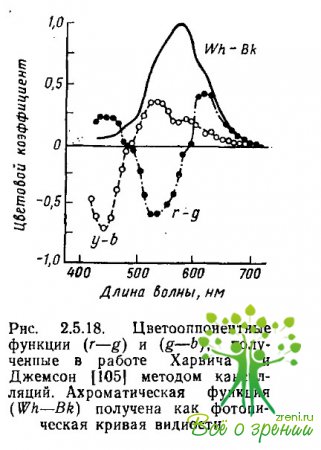
Исходным массивом экспериментальных данных, которые использовали Харвич и Джемсон для построения своей модели, послужили функции спектральной валентности четырех геринговских цветов, которые были измерены методом кансилляций (рис. 2.4.10 и 2.5.18).
Поскольку эти функции были получены для равноэнергетического спектра, Харвич и Джемсон определили матрицу линейных коэффициентов, которые связывают функции спектральной валентности с функциями смешения цветов.
(Как и большинство исследователей, Харвич и Джемсон использовали для этого функции Стандартного Наблюдателя МКО-31). Это показало, что в модели Харвича и Джемсон выполняется вся феноменология смешения цветов:
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
Последняя функция (w—s) от длины волны представляет дифференциальную активность четырех нейрональных механизмов (r, g, b, у), имеющих одинаковые значения относительной спектральной чувствительности, но разные — абсолютной, она представляет ахроматическую составляющую в модели Харвича и Джемсон. Коэффициенты k зависят от яркостного уровня стимулов и, в частности, для условий экспериментов Харвича и Джемсон они равны:
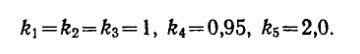
Нетрудно видеть, что, варьируя коэффициенты, можно очень гибко управлять структурой модели, но отсутствие содержательной интерпретации этих коэффициентов существенно умаляет их ценность и приближает саму модель к типу моделей ad hoc.
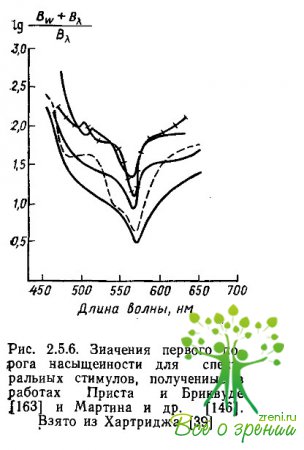
Мы не будем здесь подробно рассматривать математические выкладки, позволяющие рассчитать то большое число цветовых функций, которые приводятся в работах Харвича и Джемсон. Все подробности можно найти в руководстве Грехема. В качестве примера рассмотрим только, как измеряется в модели Харвича и Джемсон первый порог насыщенности. (Экспериментальные изме-рения этой функции уже приводились на рис. 2.5.6.)
Исходя из уравнений (4.2.1)
показатель насыщенности спектрального света определяется следующим образом:
Выражение (4.2.2) определяет вклад хроматической и ахроматической компонент в показатель насыщенности Р? для единицы яркости. Для любого выбранного значения яркости L? надо вместо единицы в числителе и знаменателе проставить это значение и тогда получится
Условия эксперимента для измерения первого порога насыщенности предусматривают, что не только ахроматическая компонента спектрального света участвует в выражении (4.2.3), но и константная ахроматическая компонента белого света, к которому подмешивается спектральный. Поэтому для смеси белого и спектрального света выражение (4.2.3) примет вид
Пороговое значение Р? также есть некоторая константа, поскольку в однородном цветовом пространстве пороговая величина везде сохраняется константной по определению. Таким образом, в уравнении (2.4) оказываются известными все параметры, за исключением L?.
Подставив для каждой длины волны в выражении (4.2.4) значения |r-g|?, |y-b|?, |w-s|? из уравнений (4.2.1) и пользуясь константами Р? и Lw можно определить L? и рассматривать его как 700 приращение от нулевого значения, т. е.
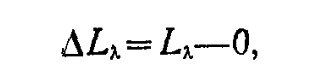
и соответственно определить для каждой длины волны отношение
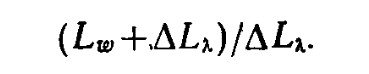
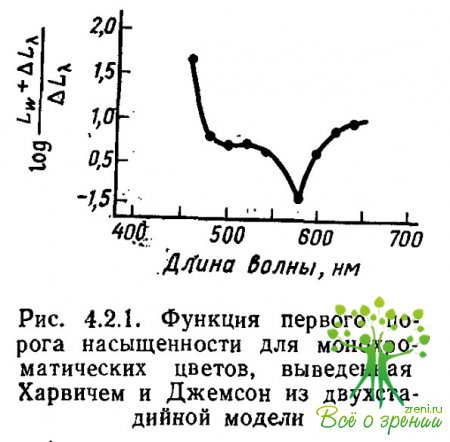
Функция (L?+?L?)/?L?, от длины волны, полученная Харвичем и Джемсон, довольно хорошо соответствует экспериментальным измерениям (рис. 4.2.1).



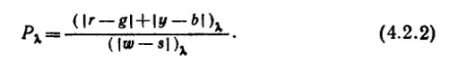
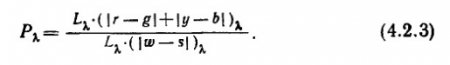
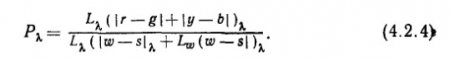
Комментариев 0