Дифференциальная чувствительность к цветовым характеристикам

Описание

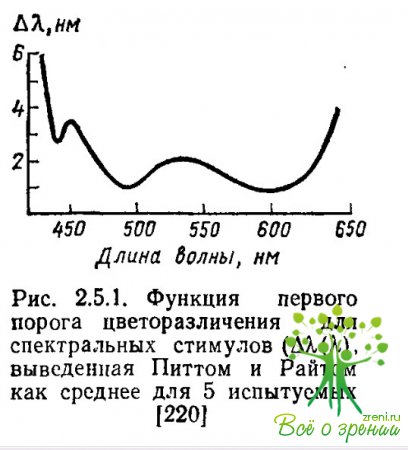
Дифференциальное цветоразличение.
Дифференциальная цветовая чувствительность определяется через несколько наиболее характерных функций. Основной функцией цветоразличения считается зависимость ?? (?), которая представляет собой непрерывную кривую при аргументе, меняющемся от 400 до 700 нм. На рис. 5.1 приводится классический образец такой функции, полученной Райтом и Питтом. Она имеет три пика наибольшей
чувствительности в областях 440—450 нм, 480—500 нм и 580— 600 нм.

Между этими областями внутри спектра чувствительность несколько уменьшается, но самое резкое понижение чувствительности происходит на краях спектра, где пороги увеличиваются в 10—20 раз.

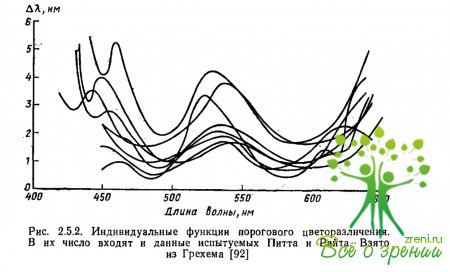
Функция ?? (?) приведенная на рис. 2.5.1, как и всякая стандартизованная функция, получена в строго фиксированных условиях (фовеальное зрение, темновая адаптация, 2-е поле с вертикальным делением на две половины и т. д.) и является только количественным ориентиром для исследователей. Она может существенно измениться, если ее измерить для конкретного испытуемого. Для сравнения на рис. 2.5.2 приводятся индивидуальные функции цветоразличения. Среди них есть и те, по которым Райт и Питт получили свою усредненную функцию.

Мы видим, что меняются не только величины дифференциальных порогов для одного и того же аргумента (сдвиг по вертикали), но и положение минимумов и максимумов чувствительности в спектре. Более того, меняется даже число пиков наибольшей чувствительности. У некоторых испытуемых, например, нет коротковолнового пика, как у остальных испытуемых, у некоторых испытуемых в крайней длинноволновой области может появиться дополнительно четвертый пик.

Однако кривая Райта и Питта — все-таки наиболее типичный случай, и поэтому все остальные модификации обычно рассматриваются как влияние индивидуальных различий или как влияние вторичных параметров цветовой стимуляции (длительности, величины, формы и т. д.). Влияние этих параметров может быть очень существенным, но, зная типичную, базисную функцию ?? (?), их всегда можно однозначно выявить.

В данной книге эти влияния рассматриваться не будут, для справок можно обратиться к руководствам Вышецки, Стайлса и Грехема.
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
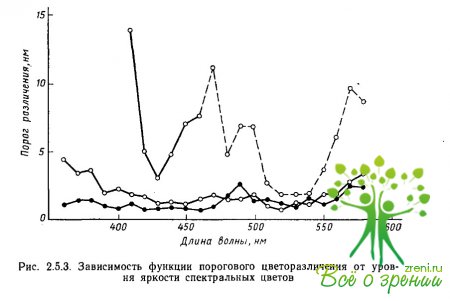
Влияние интенсивности излучения на дифференциальное цветоразличение. На рис. 2.5.3 приведены функции, полученные Сигелем для трех уровней фотометрической яркости спектральных стимулов 0,1; 1,0 и 10;0 футламберт. (Таблица соотношений между различными единицами фотометрической яркости приводится в приложении 1.)

Сравнение этих функций друг с другом иллюстрирует асимметричность изменений порогов цветоразличеиия при увеличении и при уменьшении яркости. Увеличение яркости от среднего уровня практически не меняет величину порогов по всему спектру, тогда как на низком уровне яркости чувствительность резко ухудшается, особенно в средневолновой (500— 550 нм) и коротковолновой (менее 470 нм) части спектра, а также в крайней длинноволновой части спектра (610 нм и более).

Менее всего меняется область желтых цветов (560—600 нм). Отсюда можно сделать вывод, что в некотором среднем диапазоне яркостей дифференциальная чувствительность к изменению длины волны остается постоянной, и только значительное уменьшение яркости излучения сказывается на цветоразличении.

Разложение функции чувствительности к цветоразличению на составляющие. Функция ?? (?), которую мы рассматривали выше, представляет собой на самом деле интегративную характеристику хроматической чувствительности, поскольку цветоразличение определяется, с одной стороны, через различение цветового тона и насыщенности, с другой стороны, через красно-зеленую и сине-желтую хроматические составляющие.

При построении функции испытуемый определяет общее изменение хроматичности, не специфицируя в каждом отдельном случае, по какой из составляющих производилась оценка. Провести экспериментальные измерения вклада отдельных составляющих в функцию ?? (?) слишком сложно с методической точки зрения, однако можно построить эти функции теоретически, в рамках определенной модели цветоразличения. Примерами такого типа разложения функции цветоразличения на составляющие являются графики на рис. 2.5.4 и 2.5.5.

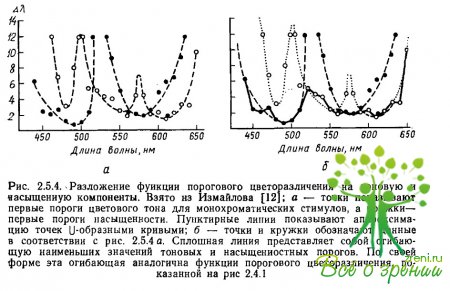
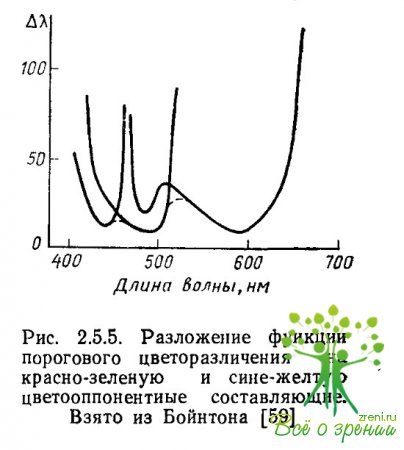
На одном из них (рис. 2.5.4) функция первого порога цветоразличения ?? (?) разлагается на тоновую и насыщенностную составляющие, а на другом (рис. 2.5.5) функция цветоразличения показана как производная от двух цветооппонентных систем r—g и b—у.

На рис. 2.5.4 а, б точками показаны пороговые значения различения цветового тона, а кружками — пороги различения насыщенности. Сплошная линия на рис. 2.5.4 б показывает, что функцию цветоразличения можно интерпретировать как огибающую нескольких простых U-образных составляющих (пунктирные линии)— двух тоновых и трех насыщенностных (рис. 2.5.4 а).

Тоновые функции имеют максимумы чувствительности (минимальные пороги) в сине-голубой (490 нм) и желтой (580 нм) областях спектра, а пасыщенностные в желто-зеленой (560 нм) и оранжево-красной (610 нм). Третья составляющая равноярких спектральных цветов по насыщенности располагается в коротковолновой части спектра с максимумом чувствительности в области 480 нм, но в этой же области спектра тоновые пороги значительно меньше, поэтому эта составляющая насыщенности существенного вклада в функцию цветоразличения не вносит.

Совершенно аналогичная картина приведена на рис. 2.5.5. Здесь функция первого порога цветоразличения построена как огибающая выходных характеристик г—g и b—у каналов. Исходные функции, приведенные на рис. 2.5.5, также представляют собой, по существу, простые U-образные функции с максимумами чувствительности в тех же самых областях спектра, что и функции на рис. 2.5.4.

Теоретические принципы, лежащие в основе анализа функций цветоразличения, представленных на рисунках 2.5.4 и 2.5.5, существенно различаются. В первом случае функция цветоразличения связывается с центральными механизмами цветового анализа излучений, характеризующими детекторный уровень цветового анализатора в рамках трехстадийной концепции цветового зрения, а во втором — с прецентральными, оппонентными механизмами анализа в рамках двухстадийной концепции цветового зрения. Эти концепции в общем виде уже рассматривались в историческом экскурсе в начале книги и будут более детально рассмотрены ниже, в третьей части книги.
Функция первого порога насыщенности. Рассмотрим следующий опыт.

Пусть фотометрическое поле освещается белым светом с интенсивностью Lw; Будем добавлять к белому свету монохроматическое излучение L?, пока испытуемый не заметит появление хроматичности в поле. Измеряя каким-либо из пороговых методов величину ?L?, необходимую для обнаружения хроматичности у разных длин волн, мы сможем построить функцию (Lw + ?L?) / ?L?.

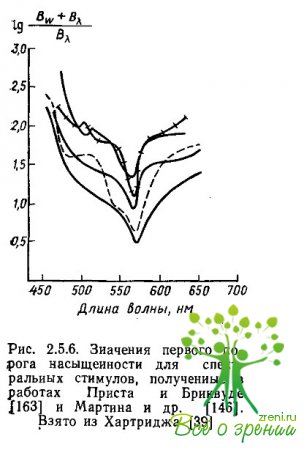
Такая функция, полученная Пристом и Бриквуде для двух испытуемых, а также Мартином, Уэбертоном и Морганом для трех испытуемых, приводится на рис. 2.5.6. Видно, что наименьшее отношение эта дробь имеет для желтых цветов спектра, а наибольшее — для синих.
Совершенно иная картина получается, если процедуру опыта изменить, добавляя к спектральному цвету белый, а не наоборот, как в предыдущем случае. При такой процедуре отношение (Lw + ?L?) / ?L? останется константным для разных длин волн. Харвич и Джемсон, исследовавшие этот феномен, объясняют его влиянием хроматической адаптации, которая неизбежна, если в начале предъявлять хроматическую компоненту смеси.

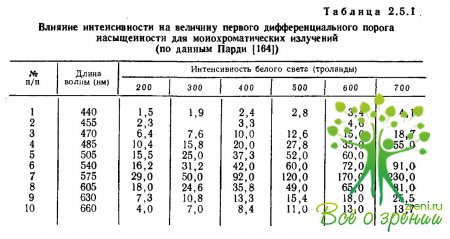
Влияние яркости на функцию первого порога насыщенности было исследовано Парди, который показал, что увеличение исходного уровня яркости белого света, к которому добавляется хроматический свет, вызывает для некоторых излучений (485—605 нм) линейное увеличение дифференциального порога тогда как для коротковолновых (менее 470 нм) и длинноволновых излучений (более 630 нм) величина порога практически не меняется. Приведенные в табл. 2.5.1 данные, взятые из работы Парди, иллюстрируют это влияние.

Дифференциальная чувствительность к яркости.
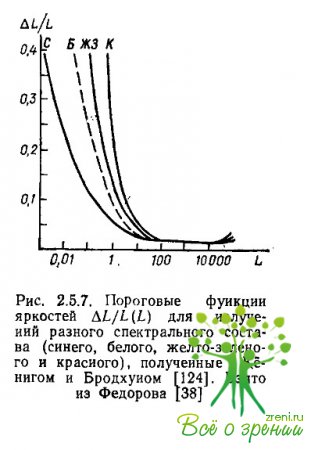
Функции дифференциальной чувствительности к изменениям интенсивности излучения были получены исследователями раньше всего. Наиболее показательными в этом плане являются данные Кенига и Бродхуна, измеривших зависимость ?L/L от L для монохроматических излучений с разной длиной волны (рис. 2.5.7). Их данные показывают, что у этих функций есть общий участок в диапазоне интенсивностей примерно 4 лог. ед., где отношение ?L/L константно, а за пределами этого участка функции расходятся.

Расхождение функций, полученных Кенигом и Бродхуном, в диапазоне очень малых интенсивностей (менее 1 лог. ед.) иногда интерпретируется как влияние палочкового аппарата сетчатки. Кинетика выцветания и восстановления палочкового пигмента (родопсина) и колбочковых пигментов (эритролаба и хлоролаба) действительно разная. В кинетическом уравнении зрительных пигментов

где k— константа, характеризующая скорость процессов выцветания и восстановления пигмента; р — количество невыцветшега пигмента; I — интенсивность света, приводящая к выцветанию пигмента; Iо — интенсивность света, которая приводит к выцветанию 1/k-той пигмента в секунду.

Для родопсина k = 400, а для хлоролаба и эритролаба 120, что означает существенно большую скорость процессов выцветания и восстановления у колбочковых пигментов.

Однако окончательной такую интерпретацию считать нельзя, поскольку пока не известны кинетические характеристики цианолаба (иигмента коротковолновых колбочек). В случае отличия константы k в уравнении (2.5.1) для цианолаба от константы для других колбочковых пигментов расхождение функции ?L/L (L) будет означать, что психофизическая функция, устанавливающая связь между воспринимаемой яркостью и интенсивностью излучения, должна включать в себя в качестве одного из параметров спектральный состав излучения. Далее, при рассмотрении данных, основанных на оценках падпороговых различий между излучениями разного спектрального состава, мы убедимся, что это действительно так.

Небольшое расхождение функций ?L/L (L) для высоких уровней интенсивности, полученное Кенигом и Бродхуном, объясняется вторичными факторами стимуляции, такими, как площадь или длительность фоновой интенсивности. Стайлс показал, что ?L/L сохраняется константным вплоть до уровня фона в 10^5 кд/м2.