Надпороговые цветовые различия

Описание
В предыдущем разделе рассматривалась дифференциальная чувствительность зрительной системы по отдельным цветовым характеристикам, таким, как светлота, насыщенность, цветовой тон.
Все рассмотренные выше функции характеризуют чувствительность зрительной системы только в одном направлении цветового пространства, от одной исходной точки к другой.
Так, измерение чувствительности к изменению длины волны излучения в одной точке спектра, например 490 нм, делается независимо от измерения чувствительности в любой другой части спектра. Далее необходимо отметить, ЧТО все ЭТИ функции Представляют собой фуНКции первого порога, т. е. определяется только один, первый шаг в данном направлении. Такой тип измерений можно назвать измерением локального цветоразличения.
Теперь мы рассмотрим новый тип цветовых измерений, характеризующих различение, во-первых, в разных направлениях цветового пространства и, во-вторых, по всей длине направления, определяемого парой цветовых точек. Этот тип измерений можно назвать измерением больших цветовых различий или исследованием глобального цветоразличения.
Эллипсы Мак Адама.
В 1942 г. Мак Адам опубликовал результаты исследования, которое проводилось по заказу «Истман Кодак Компани». Одной из целей этого исследования была разработка научного обоснования для получения патента на «желтый Кодак», который мог бы служить фирменным знаком компании. Физические измерения не могли обеспечить однозначного определения цвета вследствие феномена метамеричности световых излучений разного спектрального состава.
Поэтому Мак Адам разработал новый подход к решению проблемы, который позволял бы решить ее в общем виде, т. е. определять идентичность любых двух или более цветов. Подход основывался на выявлении общей «единицы цветоразличения», с помощью которой можно было бы измерить субъективное расстояние между любой парой цветов в цветовом пространстве.
Мак Адам выбрал 25 эталонных цветов так, чтобы они представляли все области пространства равноярких апертурных цветов, и в этих областях измерил дифференциальные пороги различения. Для каждой из 25 цветовых точек пороги определялись в восьми различных направлениях. Каждое направление задавалось двумя выравненными по фотометрической яркости светофильтрами. Испытуемый должен был подравнять по хроматичности две равнояркие половинки двухградусного фотометрического поля, на одной из которых предъявлялся эталонный цвет, а на другой — смесь из пары цветов, определяющих одно из восьми направлений.
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
Мерой дифференциальной чувствительности служило стандартное отклонение в серии подравниваний, полученных для одной и той же пары светофильтров. Для представления своих измерений Мак Адам использовал хроматическую диаграмму МКО-31. Использование хроматической диаграммы МКО, кроме удобства представления дифференциальных характеристик для равноярких цветов, позволяло Мак Адаму одновременно проверить однородность самой хроматической диаграммы МКО-31.
В случае идеальной однородности хроматической диаграммы разброс стандартных отклонений подравниваний относительно каждого эталонного цвета в восьми направлениях, заданных сравниваемыми цветами, должен был равняться нулю. Следовательно, точки, отложенные от эталонного цвета на расстоянии одного стандартного отклонения, образовали бы правильный круг, и диаметр такого круга для всех эталонных цветов должен был равняться константе.
В этом случае результаты измерений Мак Адама дали бы простую и общую для всех цветов процедуру идентификации. Два цвета можно было бы считать идентичными, если расстояние между точками, представляющими их на хроматической диаграмме МКО-31, было бы меньше или равно единице различения, полученной Мак Адамом.
Однако результаты Мак Адама показали существенную неоднородность хроматической диаграммы МКО-31 — области, образованные точками разброса подравниваемых к эталону смесей, имели эллиптическую форму и совершенно разные размеры (соотношением 1 : 30).
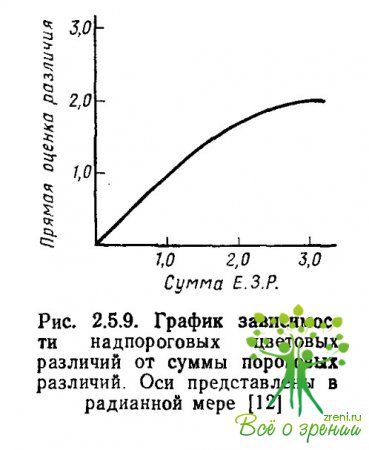
Поэтому Мак Адам построил серию номограмм, которые позволяли определять метрические коэффициенты в уравнении квадратичной формы, представляющей ?S — субъективное расстояние между цветами на хроматической диаграмме МКО-31:
где ?х и ?у — разница координат пары цветов на хроматической диаграмме ху, аij — метрические коэффициенты.
Для однородной хроматической диаграммы а11 = а22=1 и a12 = 0. В данном же случае метрические коэффициенты были так сложно связаны с координатами х и у цветовых точек, что аналитической формы для их выражения найти не удалось и Мак Адаму пришлось строить свои номограммы.
Опыты Мак Адама знаменуют собой переломный момент в. истории исследований цветового зрения. С одной стороны, они дали начало новому направлению исследований цветоразличения, связанному с построением многомерных областей чувствительности. В работах Брауна и Мак Адама, Брауна, Мак Адама и Вышецкого и Филдера было исследовано влияние на цветоразличение индивидуальных характеристик зрения, уменьшение поля сравнения, уменьшение уровня яркости, включение яркости как еще одной размерности стимулов, т. е. построение трехмерных областей дифференциальной чувствительности и т. д. С другой стороны, они дали новый метод решения проблемы перехода от пороговых различий к большим, надпороговым различиям. Эллипсы Мак Адама до настоящего времени служат одним из решающих тестов на однородность цветового пространства. Но есть еще одна проблема цветоразличения, которую также можно проиллюстрировать на результатах опытов Мак Адама.
Неаддитивность цветовых различий.
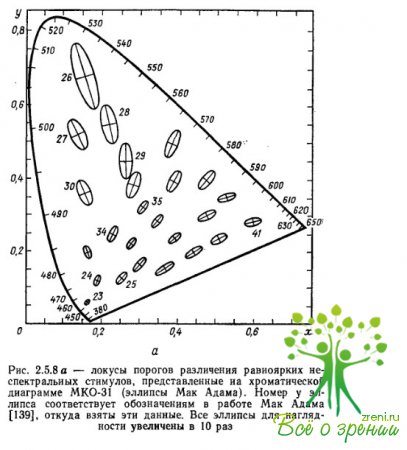
На рис. 2.5.8а, б, в величина эллипсов увеличена по отношению к диаграмме в 10 раз, т. е. расстояние от точки эллипса до центра равно 10 станд. откл. Мак Адам сделал это лишь для удобства графического представления данных.
Но такая операция могла бы иметь содержательное значение в случае, если бы хроматическая диаграмма МКО-31 была бы однородной.
Увеличение (или уменьшение) диаметра эллипса в n раз означало бы изменение уровня цветовой толерантности, т. е. изменение величины допуска на ошибку при идентификации цветов. Результаты Мак Адама показывают, что хроматическая диаграмма МКО-31 не позволяет осуществлять метрических операций с межточечными расстояниями, поскольку они не сохраняются при изменении направления измерения и при изменении места измерения. Однако, даже если оба условия выполнялись бы на хроматической диаграмме МКО-31, т. е. области неразличения образовали бы одинаковые окружности, это не означало бы еще ее однородности относительно цветовых различий. Эти условия необходимы, но недостаточны для определения однородного цветового пространства.
Дело в том, что цветовые различия обладают свойством неаддитивности. Это означает, что если мы выберем единицу цветового различия (например, одно стандартное отклонение по данным подравнивания, как это делал Мак Адам), то 10-кратное увеличение этой единицы вовсе не даст 10-кратного увеличения цветового различия.
Мак Адам, исследуя этот феномен, обнаружил, что для малых надпороговых различий наблюдается систематическая недооценка воспринимаемой величины по сравнению с вычисленной суммой нескольких малых различий. Если, например, взять два равноярких цвета А и В, смешением этих цветов получить третий цвет Б так, чтобы он имел такую же яркость, но отличался по хроматичности одинаково от А и от В, то сравнение пары А В с парой АБ или БВ показывает, что различие между цветами А и В не будет в два раза большим, чем между цветами А и Б или Б и В. Иначе говоря, для малых цветовых различий оказывается, что
Это означает, что цветоразличение характеризуется субаддитивностью. Для коррекции субаддитивности цветовых различий Мак Адам предложил использовать степенную функцию
где ?d — малое цветовое различие, а k<1.
Последующие исследования метрических свойств цветоразличения в этом направлении были проведены Джаддом. Он также получил неаддитивность малых цветовых различий, но сдругим показателем степени в выражении (2.5.4). Сравнение своих результатов с результатами Мак Адама и других авторов привело его к выводу, что степень неаддитивности прямо зависит от величины сравниваемых единиц. Чем больше исходные величины сравниваемых различий, тем больше наблюдаемая неаддитивность.
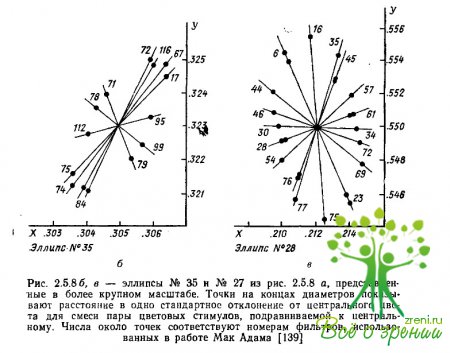
Сопоставление этих данных с данными шкалирования одновременно малых, средних и больших цветовых различий в работах Кранца, Измайлова, Соколова, Измайлова показывает, что степень неаддитивности является однотипной монотонной функцией цветового различия как для малых, так и для больших различий. На рис. 2.5.9 приводится график зависимости прямых оценок воспринимаемых различий от суммы едва заметных различий, взятый из работы Измайлова.
В третьей части книги эта модель будет рассматриваться более детально, а сейчас только отметим, что форма этой функции свидетельствует о неоднородности феномена неаддитивности. Для малых цветовых различий (вплоть до пороговых) неаддитивность почти не проявляется, и здесь показатель степени в выражении (2.5.4) будет близок к 1.
У средних цветовых различий неаддитивность выражена сильнее и соответственно показатель степени в уравнении (2.5.4) должен постепенно уменьшаться, а для наибольших цветовых различий происходит «насыщение» приращения функции, здесь увеличение числа порогов практически не меняет величины воспринимаемого различия. Это объясняет трудности, с которыми сталкиваются исследователи, когда пытаются применять к измерению больших различий методологию, разработанную для измерения пороговых различий.


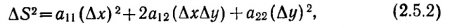


Комментариев 0