Субъективное цветовое пространство

Описание

Измерение больших цветовых различий.
Новая методология шкалирования цветовых различий сформировалась в 60-х и 70-х гг. благодаря интенсивному развитию нового направления в математической психологии, называемого многомерным шкалированием. Интересно отметить, что развитие методов многомерного шкалирования оказалось очень тесно связано с исследованиями цветового зрения.


Хотя некоторые процедуры измерения надпороговых различий между стимулами применяются с незапамятных времен, по- настоящему, как психофизические методы, они стали разрабатываться только в нашем веке, главным образом в работах Стивенса и его сотрудников, а также в работах шведской психофизической школы. Однако в исследованиях цветового зрения эти методы не получили широкого распространения.

Наиболее известными измерениями такого рода являются функции видимой светлоты поверхности, аргументом которых служит яркостный коэффициент отражения, меняющийся от нуля (идеальный черный) до 100% (идеальный белый), а также функции насыщенности монохроматических цветов, аргументом которых является чистота цвета в процентах. Примером типичного отношения к оценкам больших цветовых различий может служить точка зрения Вышецки и Стайлса — одних из наиболее авторитетных представителей цветовой науки, изложенная в их руководстве по цвету:

«... Как бы ни оценивалась точность суждений об относительной величине двух цветовых различий, она значительно уступает точности цветового подравнивания ... Когда различия в светлоте или хроматичности становятся большими, наблюдателю очень трудно оценить их величину. В общем оценка очень больших различий в цвете представляет малую практическую ценность. Принципиальный интерес представляет изучение малых различий и различий, которые наблюдатель находит едва заметными или пороговыми, поскольку последние могут рассматриваться как естественные единицы при измерении больших различий».

Как видно из этой ссылки, существенным недостатком методов измерения больших цветовых различий считается малая достоверность данных. Этот справедливый упрек имеет отношение не только к оценкам цветовых различий, но и вообще к методам прямого оценивания величины стимула, а для науки о цвете, где имеется внушительный массив работ, проведенных колориметрическими и пороговыми методами, результаты измерения больших цветовых различий кажутся особенно незначительными и чаще именно поэтому сами методы рассматриваются как второстепенные.

Но внимательный анализ данных показывает, что все блестящие достижения колориметрических и пороговых методов связаны главным образом с построением частных цветовых функций, которые рассматривались в предыдущих разделах книги. В то же время существует ряд более общих проблем, которые до настоящего времени все еще не имеют окончательного решения.

Одной из таких фундаментальных проблем в психофизике цветового зрения является проблема построения однородного цветового пространства, в котором точки представляют отдельные апертурные цвета, а расстояния между точками пропорциональны воспринимаемым различиям между цветами.

В западноевропейской и американской литературе для обозначения этого свойства цветового пространства — быть одинаковым во всех участках относительно воспринимаемых различий — применяется термин «uniform» — однородное (например, Джадд; Джадд и Вышецки; Вышецки и Стайлс —«uniform color scale», «uniform color space»). В отечественной литературе чаще используется термин «равноконтрастное» (Мешков), поэтому при переводе зарубежной литературы по восприятию цвета термин «uniform» также переводят как «равноконтрастное» (см., например, Джадд, Вышецки).
[banner_centerrs] {banner_centerrs} [/banner_centerrs]

В наших работах используется термин «изотропное цветовое пространство», чтобы подчеркнуть однородность относительно цветоразличения во всех направлениях пространства.

Как показывает опыт, решить эту проблему в традиционных терминах колориметрических или пороговых измерений очень мало надежды. Существуют трудности, связанные с предположением, которое вслед за Фехнером делает большинство исследователей, что метрика малых и больших различий одна и та же, и в; этом смысле большое различие есть не что иное, как аддитивная комбинация малых различий.

Мы уже видели, что это предположение не соответствует экспериментальным данным. С нашей точки зрения, проблему построения изотропного цветового пространства надо решать не столько по данным о локальной метрике цветового пространства, характеризующей пороговое цветоразличение, но главным образом на основе данных о глобальной метрике, которая определяется структурой больших цветовых различий.

Построение цветового пространства методами многомерного шкалирования.
Метод многомерного шкалирования позволяет исследовать две основные проблемы, возникающие при построении цветового пространства, — определение базисной размерности и метрики. Как мы увидим ниже, хотя математически эти характеристики пространства совершенно независимы, в цветовом пространстве они связаны через ограничения содержательного характера.

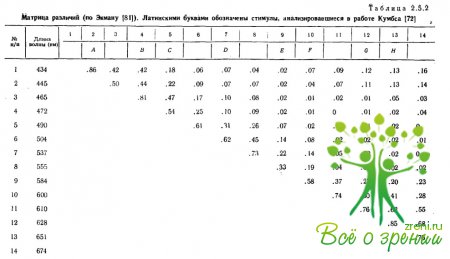
Одну из первых работ по анализу матрицы сходств между апертурными цветами провел в 1954 г. Экман.
14 спектральных стимулов равной интенсивности, полученных с помощью фильтров, попарно предъявлялись испытуемым, которые оценивали степень качественного сходства в рангах от О (полное отсутствие сходства) до 4 (идентичность). Оценки сходства усреднялись и сводились в матрицу (14x14) (табл. 2.5.2). Элементы матрицы линейно трансформировались в шкалу от нуля до единицы, и новая матрица анализировалась с помощью центроидного метода.
Экман на основе матрицы сходства выделил пять факторов, которые он интерпретировал как основные признаки цветового тона: фиолетовый, синий, зеленый, желтый и красный. Построив: графики веса фактора (ордината) относительно длины волны стимулов (абсцисса), Экман получил для этих факторов кривые, которые он соотносил с характеристиками цветовых модуляторов сетчатки, полученных Гранитом.

Интерпретация Экмана была подвергнута критике как слишком сложная, и ряд авторов попытались проанализировать данные Экмана различными методами многомерного шкалирования. Рассмотрим данные Кумбса, который вновь проанализировал матрицу сходств, полученную Экманом.

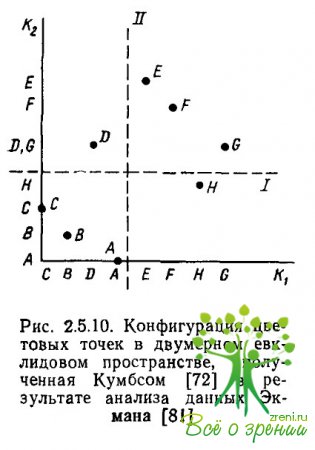
Из 14 стимулов, использованных Экманом, Кумбс взял только 8, но так, чтобы в них входили все цвета, которые трактовались Экманом как основные факторы. Цвета, выбранные Кумбсом, отмечены в табл. 2.5.2 дополнительными буквами А, В, С, D, Е, F, G, Н. Для анализа матрицы сходств Кумбс использовал неметрическую модель многомерного шкалирования, развиваемую Хейсом и Беннетом в 1956 г., и получил двумерное пространство, в котором круговая последовательность стимулов соответствует изменению длины волны (рис. 2.5.10).

Вращение данного пространства позволило Кумбсу соотнести одну ось пространства с красно-зеленым направлением, а другую — с желто-синим, что хорошо согласуется с оппонентной структурой цвета. Кумбс делает вывод о достаточности двумерного евклидова пространства для описания данных цветоразличения.

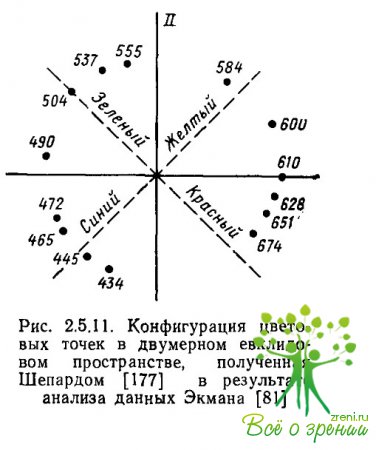
Аналогичные результаты получил Шепард при анализе матрицы сходств Экмана неметрическим мно-гомерным шкалированием. Расположение 14 цветовых точек в двумерном евклидовом пространстве, которое получил Шепард, так же, как и в работе Кумбса, имеет явную оппонентную структуру (рис. 2.5.11). Четыре фактора — «красный», «зеленый», «синий» и «желтый» — организованы в две биполярные системы, причем «синий» фактор включает в себя и синие и фиолетовые цвета.

Однако результаты Кумбса и Шепарда не так отличаются от результатов Экмана, как это кажется на первый взгляд. В частности, основные характеристики цвета, выделенные здесь (красный, зеленый, синий, желтый), такие же, как у Экмана, и лишь организованы более компактным образом в биполярной системе координат. Что касается пятого фактора, то его действие элиминировать можно только в неметрическом престранстве, которое строили Кумбс и Шепард, а в случае линейного метрического решения, которое проводил Экман, его влияние остается довольно значимым.

Это иллюстрируется в работе Стоун и др., в которой была несколько модифицирована обработка исходных данных Экмана. Усредненная матрица сходств (nxn), где n — число стимулов, с единицами по главной диагонали трактовалась как множество n-столбцовых векторов, каждый из которых состоит из n компонент. Попарный коэффициент корреляций между всеми векторами дает n (n—1)/2 корреляций.
Они представляют собой матрицу корреляционных сходств. Оценки корреляционного сходства показывают полное тождество (при r=1), отсутствие сходства (r = 0) и противоположность как систематическое несходства (r= — 1). Полученная матрица сходств отличается от обработки Экмана тем, что она выявляет не только положительную корреляцию, но и отрицательную тоже.

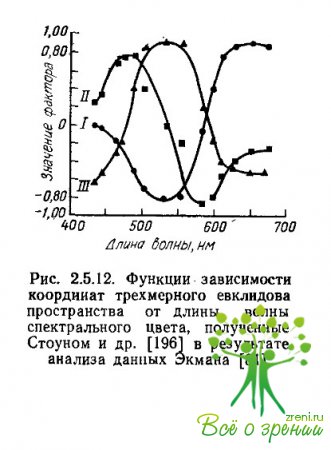
Матрица корреляционных сходств обрабатывалась методом главных компонент, и было выделено три фактора. При этом два из них были биполярными. По первому фактору разводились красные и зеленые стимулы, а по второму — синие и желтые. Третий фактор имел сходство с фактором «фиолетовый» у Экмана, однако косое вращение этого фактора позволило интерпретировать его иначе.

После этого вращения был построен график зависимости весов по трем факторам от длины волны (рис. 2.5.12). График показывает качественное сходство кривых с оппонентными характеристиками цветового зрения по Харвичу и Джемсон. Первый фактор интерпретируется как красно-зеленая характеристика, второй — как сине- желтая, а третий — как бело-черная. Работы по анализу матрицы сходств Экмана различными методами показывают в общем непротиворечивые результаты.

Линейное решение приводит к пяти факторам — красный, зеленый, желтый, синий и фиолетовый (или белый), которые могут быть организованы в трехмерном пространстве в биполярную систему декартовых координат. Неметрическое решение дает более простое двумерное пространство, организованное из четырех факторов, но это происходит за счет ослабления соответствия с исходными данными.

Вопрос базисной размерности цветового пространства специально рассматривался Крускалом, который анализировал неметрическим многомерным шкалированием данные по цветоразличению стимулов равной яркости, но разного цветового тона и насыщенности. Варьируя показатели степени (р) в выражении, характеризующем метрику пространства от 1 до 5, Крускал определил, как мы уже говорили выше, что наилучшее соответствие исходным данным дает метрика с р = 2,5.

То есть размерность субъективного пространства цветоразличения для цветов равной яркости может оказаться больше двух.
Основательное подтверждение этого положения можно найти в работе Шепарда и Кэрролла, в которой как один из частных вопросов рассматривалась проблема определения базисной размерности субъективного пространства цветоразличения равноярких цветов.

Эту проблему авторы рассматривали на основании одной серии экспериментальных данных Бойнтона и Гордона. Мы подробно остановимся на этих опытах, поскольку полученный Бойнтоном и Гордоном экспериментальный материал будет анализироваться нами в дальнейшем с различных точек зрения и в результате этого анализа будут сделаны существенные выводы о структуре субъективного пространства цветоразличения.

Бойнтон и Гордон исследовали зависимость цветоразличения от яркости стимулов у трех нормальных испытуемых методом называния цветов. Испытуемым предъявлялись 23 монохроматических стимула с длиной волны от 440 до 660 нм, с шагом в 10 нм. Испытуемые должны были произвести классификацию стимулов по четырем цветовым классам с названиями: синий, зеленый, желтый, красный.

Если стимул оценивался как промежуточный между двумя классами, то он назывался двойным названием, например, «сине-зеленый», причем на первое место ставилось то название, цвет которого в стимуле был субъективно более выражен. При обработке результатов всем классам приписывались веса в зависимости от места. Если стимул принадлежал только к одному классу, то соответствующему названию для этого стимула приписывался вес 3, если для обозначения стимула использовалась комбинация из двух названий, как в примере с сине-зеленым цветом, то первому классу «синий» приписывается вес 2, а второму классу «зеленый»—вес 1.

Стимулы предъявляются по 25 раз каждый, и взвешенная частота отнесения стимула к каждому из классов служит мерой субъективной оценки стимула. Откладывая по оси абсцисс длину волны стимула, а по оси ординат меру субъективной оценки по данному классу, Бойнтон и Гордон строили функцию называния цветов. Меняя яркость стимулов "на двух уровнях 100 и 1000 тролланд, Бойнтон и Гордон могли судить по изменению функции называния цветов о зависимости цветоразличения от уровня яркости.

Для того чтобы применить к этим данным аппарат многомерного шкалирования, Шепард и Кэрролл рассматривали каждый стимул как вектор называний. Компонентами вектора служили взвешенные частоты называний. Число компонентов определяется числом классов, поэтому все векторы были в данном случае четырехкомпонентными.

Между векторами вводилась, некоторая мера близости («сити-блок» в одном случае и евклидова мера в другом) и вычислялись все попарные близости. Матрица этих n (n—1)/2 близостей, где n — это число стимулов, вычислялась для данных на уровне яркости в 100 тролландов,. усредненных по трем испытуемым. Полученная матрица анализировалась различными методами многомерного шкалирования.

Было показано, что пространственная модель не зависит от выбранной меры близости между векторами реакций. Решение, когда исходные различия интерпретировались в евклидовой метрике, не отличалось от решения, когда эти же различия интерпретировались в «сити-блок» метрике. Кроме того, пространственная модель оказалась независимой и от используемого для анализа алгоритма многомерного шкалирования. Эти результаты привел» авторов к выводу о существовании жесткости структуры пространства цветоразличения.

При этом оказалось, что в зависимости от того, какой принимали критерий приближения межточечных расстояний к исходным мерам близости, менялась размерность полученного пространства.
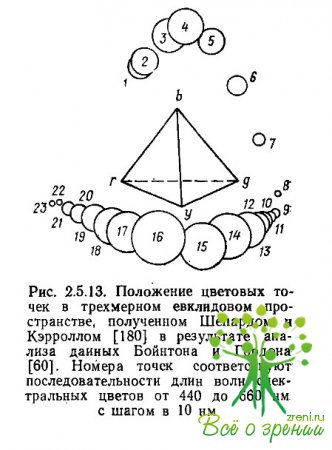
В случае требования глобальной линейности между исходными мерами близости и межточечными расстояниями минимальная размерность полученного евклидова пространства равнялась трем. В трехмерном пространстве 23 точки, представляющие монохроматические цвета, располагались так, что линия, соединяющая последовательно от первого до двадцать третьего стимула, образовывала одномерную криволинейную траекторию с изгибами в области синего цвета, зеленого и желтого (рис. 2.5.13).

Поскольку Шепард и Кэрролл ориентировались на физическую переменную в стимуляции, а в данном случае это была только длина волны, то трехмерное решение не совмещалось с такой интерпретацией.

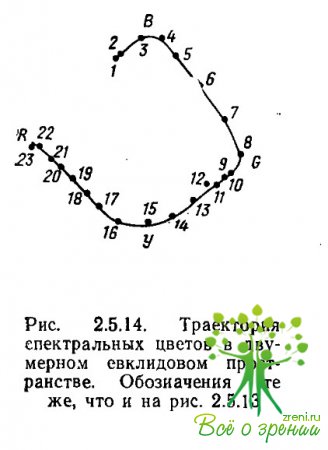
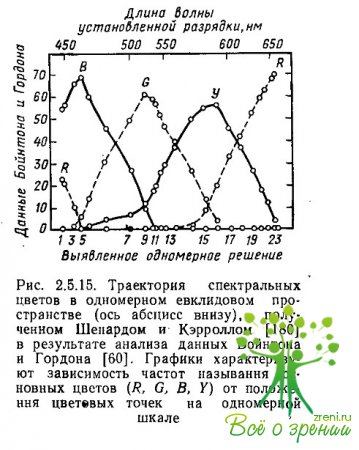
Ограничив отношение между исходными данными и межточечными расстояниями требованием глобальной монотонности, Шепард и Кэрролл для этих же данных получили уже двумерное пространство (рис. 2.5.14). И в этом случае все точки явно лежали на единственной кривой, изгибы которой приходились на те же самые области синего, зеленого и желтого цветов. А когда условие глобальной монотонности было заменено условием локальной монотонности, все точки удалось расположить на прямой линии. Это единственное измерение можно было интерпретировать как субъективную характеристику физической переменной — длины волны стимула (рис. 2.5.15).

Анализируя полученные результаты, Шепард и Кэрролл обращают внимание на реципрокные отношения между простотой самого пространственного представления исходных данных и простотой той связи, которую устанавливает это представление с исходными данными. В первом случае более сложное трехмерное решение имеет преимущество линейной связи с исходными данными, тогда как самое простое одномерное решение платит за свою экономичность крайней нелинейностью связи с исходными данными.

К приведенным выше положениям необходимо добавить еще один содержательный критерий определения истинной размерности субъективного пространства — критерий нейрофизиологической интерпретации полученных результатов. В этом смысле представляется маловероятным существование единственного сенсорного механизма, функционирующего по такому сложному принципу, как это определяется одномерным решением. Многочисленные данные по работе цветового анализатора скорее говорят о наличии нескольких, но в общем-то простых и однотипно функционирующих механизмов, как это предполагается в трехмерном решении.

Однако трехмерное решение сталкивается с существенной трудностью при традиционной интерпретации субъективных характеристик аппертурных цветов. Общепринятое представление состоит в том, что равнояркие цвета характеризуются только двумя независимыми субъективными переменными — это, например, цветовой тон и насыщенность или две хроматические оппонентные системы и т. д.