МАТЕМАТИЧЕСКАЯ ПСИХОФИЗИОЛОГИЯ ЦВЕТОВОГО ЗРЕНИЯ | Модель Гельмгольца

Описание
Автором первой математической модели различения цветов был Герман фон Гельмгольц. Он разработал ее незадолго до смерти в 1894 г., основываясь на своей теории цветового зрения. На модель Гельмгольца уже много лет ссылаются только как на начальную точку в истории математических моделей цветоразличения.Действительно, модель Гельмгольца очень быстро обнаружила свою несостоятельность в решении проблемы цветоразличения, но тем не менее она имеет не только исторический, но и теоретический интерес. Целый ряд идей, лежащих в основе модели Гельмгольца, без изменений входит во все последующие модели.
Такова, например, идея применения в качестве модели различения цветов метрического многомерного пространства, в котором точки представляют отдельные цвета, а межточечные расстояния — соответственно цветовые различия. Затем Гельмгольцу принадлежит также идея физиологической интерпретации осей цветового пространства. В связи с этим будет полезно рассмотреть главные положения модели Гельмгольца.
Построение модели Гельмгольц начал с решения следующей проблемы: как можно различать цвета, основываясь на изменении интенсивности трех базисных процессов R, G, В, протекающих в приемниках сетчатки?
Пусть ?IR, ?IG и ?IB представляют минимальные величины из-менения интенсивности, приводящие к активации соответствующие приемники, а ?S — величина минимального цветового различия. Тогда ответом на вопрос будет следующее уравнение:
[banner_centerrs] {banner_centerrs} [/banner_centerrs]
Каким психофизиологическим требованием должна удовлетворять функция F в выражении (4.1)? Во-первых, ?S не может быть отрицательным, поскольку цветовое различие не может быть меньше нуля (т. е. различия двух идентичных цветов). Далее, при ?S = 0 должно выполняться ?IR = ?IGс = ?IB=0, поскольку цветовое различие может исчезнуть только в том случае, если ни один из приемников не меняет своей активности. Самая простая функция, которая удовлетворяет таким требованиям, это:
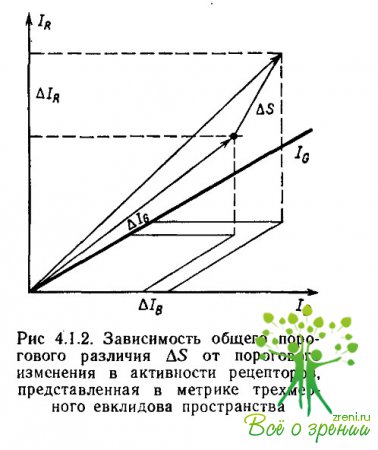
что в геометрических терминах может быть представлено как расстояние в трехмерном евклидовом пространстве (рис. 4.1.2).
Следующий вопрос, на который отвечал Гельмгольц, касалсяг психофизической характеристики чувствительности приемников сетчатки. Здесь Гельмгольц принял Фехнеровскую идею
Константы ?, ?, ? интерпретировались Гельмгольцем как характеристики «собственного света» сетчатки, а термин Н был введен для сохранения закона Вебера при максимальных уровнях яркости света.
Проверку своей модели Гельмгольц начал с расчета величины расстояния, соответствующей едва заметному различию. Для этого он упростил задачу, перейдя к измерению только яркостного различия между цветами.
Допустим, мы изменили яркость цвета на некоторую величину. Различие между бывшим и новым цветами также выражается как ?S. При этом изменении активность цветоприемников изменяется в одном и том же отношении так, что
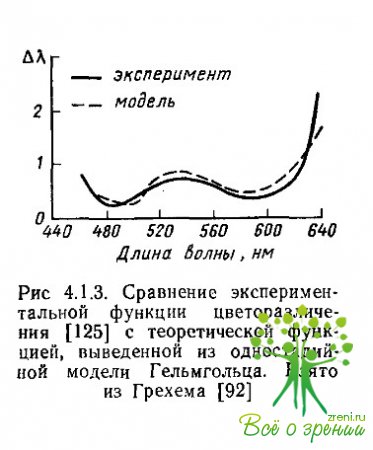
Использовав теперь для расчета экспериментальные данные Кенига и Дитеричи по различению яркостей, Гельмгольц вывел, что величина ?S равна 0,018. Эту константу он использовал для вычисления функции цветоразличения ??(?) и получил хорошее соответствие между теоретической и экспериментальной функциями. На рис. 4.1.3 показаны две эти функции, сплошная линия представляет экспериментальные измерения Кенига и Дитеричи, а пунктирная — расчеты в модели Гельмгольца.
Когда же Гельмгольц попытался вывести из своей модели функции спектральной чувствительности первичных приемников, которые были бы согласованы с уже выведенной функцией цветоразличения, он потерпел неудачу. Полученные функции спектральной чувствительности имели два пика и очень мало соответствовали характеристикам приемников, на которых базировалась трехкомпонентная теория. Такие функции спектральной чувствительности, хорошо согласующиеся с требованиями трехкомпонентной теории, уже были выведены Кенигом и Дитеричи на основании экспериментов по смешению цветов.
После Гельмгольца многие исследователи пытались найти более удачное решение, модифицируя различные параметры модели. В частности, Шредингер модифицировал модель Гельмгольца, заменив выражение (4.1.3) следующей формой:
Шредингер вывел из своей модели функции спектральной чувствительности первичных приемников, которые были согласованы с данными смешения цветов Кенига и Дитеричи, однако в этом случае оказалось невозможным вывести функцию цветоразличения из модели Шредингера.
Таким образом, модели Гельмгольца и Шредингера показывали, что функция цветоразличения не имеет прямой связи с функциями чувствительности приемников сетчатки, что служило решающим аргументом для отвержения трехкомпонентной одностадийной теории цветового зрения.


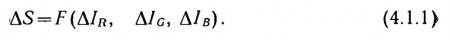
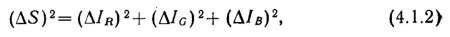
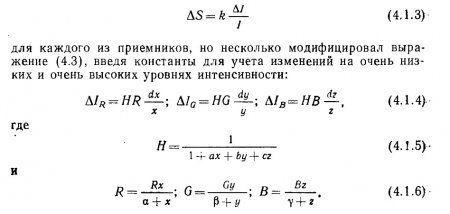


Комментариев 0